De-dimensionalization

De-dimensioning or de-dimensioning is the partial or complete removal of dimensions (such as units of measurement ) from a physical equation by a suitable substitution of variables. With the help of dimensionless variables and constants with dimensions, effects that result from the choice of the system of units can be eliminated and intrinsic constants of the system, such as characteristic lengths , times or frequencies, can be found. The technique is therefore suitable for simplifying systems of differential equations .

The de-dimensionalization is related to the dimensional analysis and the dimensional observation .

Properties and advantages of dimensionless equations

In some physical systems, the term scaling is used as a synonym for de-dimensionalization, to indicate that some quantities are not measured in a general system of units such as the SI units , but rather relative to a unit given by the system under consideration. These units are called “intrinsic” or “characteristic” quantities of the system. Such a characteristic variable can be, for example, an average lifetime or the period of oscillation of a pendulum, so that the time is measured in a correspondingly scaled system as a multiple of these variables.

The Reynolds number shows the dependency of 4 dimensional quantities in a dimensionless quantity and thus enables a reduction of the dimensionality of the Moody diagram.

In the case of de-dimensionalization, dimensionless key figures arise in the equation , for example in fluid mechanics the Reynolds number (from the de-dimensionalization of the Navier-Stokes equation ), the Euler number or the Prandtl number . These reference variables are chosen so that the new dimensionless variables are typically of the order of one. The dimensionless formulation therefore defines what “small” means, namely when the dimensionless quantity is less than one.

By completely de-dimensionalizing an equation, the parameters of the system can be reduced by combining them into dimensionless groups. With the help of these dimensionless groups, characteristic constants of a system can then be discovered, such as resonance frequencies, lengths or times. By combining the parameters into dimensionless groups, systems can be compared with one another. Two systems, which in reality have the same behavior but a different absolute dimension, for example a spring pendulum and an oscillating circuit, can be reduced to the same dimensionless system of equations by de-dimensionalization.

De-dimensionalization has to be distinguished from the conversion of extensive quantities in an equation into intensive ones, since the results of this procedure are still subject to units.

Action

There are often several ways to convert a dimensional equation into a dimensionless equation, although the optimal choice is initially unclear. An unknown system of differential equations can therefore be de-dimensionalized with the following steps:

(1) Identify all dependent and independent variables.

(2) Every independent dimensional variable is replaced by a product of a dimensionless quantity and a dimensional reference variable according to . The value of the reference variable is later determined so that the dimensionless quantity is of the order of one. ${\displaystyle \varphi }$ ${\displaystyle {\hat {\varphi }}}$ ${\displaystyle \varphi _{\mathrm {c} }}$ ${\displaystyle \varphi ={\hat {\varphi }}\cdot \varphi _{\mathrm {c} }}$

(3) With the help of the chain rule , all dimensional derivatives are expressed by derivatives of the dimensionless quantities according to another dimensionless quantity.

(4) The system of differential equations now generally consists of products of dimensionless terms, which are calculated from the dimensionless quantities and their derivatives, and dimensional coefficients, which are calculated from parameters and the reference variables. The dimensioned coefficients are replaced by dimensionless groups by dividing each equation by the coefficient before the term of the highest order or another quantity of equal dimension.

(5) According to the above assumption, every dimensionless quantity as well as its derivative is of the order of one. The reference variables are therefore set in such a way that as many dimensional coefficients as possible also have the order of magnitude one. A term in the equation is “small” if the dimensionless group is less than one. This makes it possible to specify in which systems a term is negligible.

(6) A new variable is introduced for each remaining dimensionless group so that the system of equations can be written as a function of these variables.

Examples

First order differential equation

A first-order differential equation with constant coefficients is considered ( ) ${\displaystyle a,b,A}$

${\displaystyle a{\frac {\mathrm {d} x}{\mathrm {d} t}}+bx=Af(t)}$

which is de-dimensionalized according to the above scheme:

(1) The equation contains an independent variable and a dependent variable . ${\displaystyle t}$ ${\displaystyle x}$

(2) Replace and . ${\displaystyle \textstyle x={\hat {x}}\cdot x_{\mathrm {c} }}$ ${\displaystyle \textstyle t={\hat {t}}\cdot t_{\mathrm {c} }}$

(3) Replace the derivative

${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}={\frac {x_{\mathrm {c} }}{t_{\mathrm {c} }}}{\frac {\mathrm {d} {\hat {x}}}{\mathrm {d} {\hat {t}}}}}$

and define

${\displaystyle \textstyle {\hat {f}}({\hat {t}}):=f({\hat {t}}\cdot t_{\mathrm {c} })}$

(4) The result

${\displaystyle a{\frac {x_{\mathrm {c} }}{t_{\mathrm {c} }}}{\frac {\mathrm {d} {\hat {x}}}{\mathrm {d} {\hat {t}}}}+bx_{\mathrm {c} }{\hat {x}}=A{\hat {f}}({\hat {t}})}$

is divided by the coefficient before the term with the highest order derivative. ${\displaystyle \textstyle a{\frac {x_{\mathrm {c} }}{t_{\mathrm {c} }}}}$

(5) As a result

${\displaystyle {\frac {\mathrm {d} {\hat {x}}}{\mathrm {d} {\hat {t}}}}+\left({\frac {bt_{\mathrm {c} }}{a}}\right){\hat {x}}=\left({\frac {At_{\mathrm {c} }}{ax_{\mathrm {c} }}}\right){\hat {f}}({\hat {t}})}$

the parameters appear as two dimensionless groups as well . The first contains only the characteristic variable and is therefore set as the first one: ${\displaystyle \textstyle {\frac {bt_{\mathrm {c} }}{a}}}$ ${\displaystyle \textstyle {\frac {At_{\mathrm {c} }}{ax_{\mathrm {c} }}}}$ ${\displaystyle t_{\mathrm {c} }}$

${\displaystyle {\frac {bt_{\mathrm {c} }}{a}}=1\Rightarrow t_{\mathrm {c} }={\frac {a}{b}}.}$

It follows for the second group

${\displaystyle {\frac {At_{\mathrm {c} }}{ax_{\mathrm {c} }}}={\frac {A}{bx_{\mathrm {c} }}}=1\Rightarrow x_{\mathrm {c} }={\frac {A}{b}}.}$

(6) The resulting dimensionless equation is independent of dimensional parameters:

${\displaystyle {\frac {\mathrm {d} {\hat {x}}}{\mathrm {d} {\hat {t}}}}+{\hat {x}}={\hat {f}}({\hat {t}}).}$

Mass-spring system

A mass-spring system consisting of a horizontally displaceable mass m in the x -direction on a spring with a spring constant k and a vibration damper with a damping constant B attached to a wall. The external force F that deflects the system from the rest position is zero.

For a mass-spring system (see figure) the following differential equation can be set up:

${\displaystyle m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+B{\frac {\mathrm {d} x}{\mathrm {d} t}}+kx=0}$

With

• ${\displaystyle x}$ the deflection from the rest position in meters [m]
• ${\displaystyle t}$ the time in seconds [s]
• ${\displaystyle m}$ Mass in kilograms [kg]
• ${\displaystyle B}$ Damping constant [kg s ⁻¹ ]
• ${\displaystyle k}$ Spring constant [kg s ⁻² ]

After steps (1) to (4), the dimensionless system of equations is obtained

${\displaystyle {\frac {\mathrm {d} ^{2}{\hat {x}}}{\mathrm {d} {\hat {t}}^{2}}}+{\frac {Bt_{\mathrm {c} }}{m}}{\frac {\mathrm {d} {\hat {x}}}{\mathrm {d} {\hat {t}}}}+{\frac {kt_{\mathrm {c} }^{2}}{m}}{\hat {x}}=0}$

(5) The characteristic time can be chosen as what corresponds to a period of the undamped oscillation. ${\displaystyle \textstyle t_{\mathrm {c} }={\sqrt {\frac {m}{k}}}}$

(6) What remains is a dimensionless system of equations called a damped harmonic oscillator , with a dimensionless group , where the dimensionless parameter is called the degree of damping : ${\displaystyle \textstyle 2D={\frac {B}{\sqrt {mk}}}}$ ${\displaystyle D}$

${\displaystyle {\frac {\mathrm {d} ^{2}{\hat {x}}}{\mathrm {d} {\hat {t}}^{2}}}+2D{\frac {\mathrm {d} {\hat {x}}}{\mathrm {d} {\hat {t}}}}+{\hat {x}}=0}$

Electrical oscillating circuit

A resonant circuit consisting of an ohmic resistor R , a capacitor with capacitance C and a coil with inductance L.

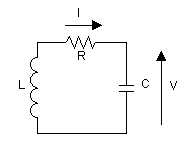
The following differential equation can be set up for an electrical oscillating circuit (see figure):

${\displaystyle LC\cdot {\frac {\mathrm {d} ^{2}i}{dt^{2}}}+RC\cdot {\frac {\mathrm {d} i}{\mathrm {d} t}}+i=0}$

With

• ${\displaystyle i}$the electrical current in amperes [A]
• ${\displaystyle t}$ the time in seconds [s]
• ${\displaystyle C}$the electrical capacitance in farads [A ² s ⁴ kg ⁻¹ m ⁻² ]
• ${\displaystyle R}$the electrical resistance in ohms [A ⁻² s ⁻³ kg m ² ]
• ${\displaystyle L}$the electrical inductance in Henry [A ⁻² s ⁻² kg m ² ]

After steps (1) to (6) one also obtains a damped harmonic oscillator as a dimensionless system of equations

${\displaystyle {\frac {\mathrm {d} ^{2}{\hat {i}}}{\mathrm {d} {\hat {t}}^{2}}}+2D{\frac {\mathrm {d} {\hat {i}}}{\mathrm {d} {\hat {t}}}}+{\hat {i}}=0}$

If the dimensionless damping constant of the electrical oscillating circuit corresponds to the damping constant of the mass-spring system, both systems show the same behavior. ${\displaystyle D}$

See also

• Size of dimension number

literature

• CC Lin, LA Segel: Mathematics Applied to Deterministic Problems in the Natural Sciences . SIAM, 1988.

Individual evidence

1. ^ J. Struckmeier: Mathematical modeling. 2.1. Scaling, de-dimensionalization and small parameters. P. 45 , accessed on May 14, 2017 . 
2. ^ ^{A b c d e} Steven H. Strogatz: Nonlinear Dynamics and Chaos . Westview Press, 2000, ISBN 0-7382-0453-6 , pp. 64 .