Edge coloring
In graph theory , edge coloring is a mapping that assigns an (abstract) color to each edge of a graph. Edge coloring is called valid or permissible if the following applies to each node of the graph: All edges adjacent to the node have different colors.
The term is closely related to knot coloring .
definition
For an undirected multigraph , mapping the set of edges into the set of natural numbers is called an edge coloring of . The elements from are called colors in this context . One calls valid or admissible if for any two adjacent edges and it holds that . Has an edge coloring so that at most colors appear in the image area of , it is called - edge coloring .
The smallest for which a graph can be edge-colored is called the chromatic index , the edge-coloring number or the edge- chromatic number of the graph and is usually referred to as.
properties
According to Vizing's theorem , the chromatic index of a simple graph is at least as large as its maximum degree, but at most one greater than this, i.e. formally:
Graphs with are called class 1 graphs , graphs with are called class 2 graphs , since the estimation of the theorem does not apply to multigraphs , multigraphs are called class 2 graphs if applies. To decide whether a graph is class 1 or class 2 ( classification problem ) is NP-complete . This means that although the maximum degree is easy to determine and the chromatic index can only take one of two possible values, the problem of determining exactly this one value for a given graph is NP-difficult .
For bipartite graphs is . This means that all bipartite graphs are class 1 graphs.
example
On a cyclic graph , the edges can be colored with two colors if the length of the cycle is even. However, if the length is odd, then three colors are needed.
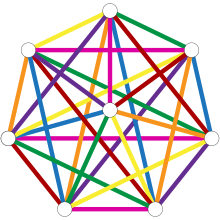
A complete graph with nodes can be colored edge if is an even number. This is a special case of Baranyai's theorem . In this case, Soifer provides the following geometric construction of a coloring: There are nodes at the corners and in the middle of a regular polygon with corners. For each color class, connect an edge from the center to one of the nodes and all perpendicular edges that connect pairs of nodes. However, if is odd, then colors are needed: each color can only be used for edges, one of the total.
Several authors have examined the edge coloring of the odd graphs, - regular graphs in which the nodes represent teams of players selected from a set of players, and in which the edges represent possible encounters between these teams, with one player as the "odd man" who runs the game. The case gives the well-known Petersen graph . Biggs explains the problem for . The players want to find a schedule for these encounters so that each team plays each of their 6 games on different days of the week, with all teams having Sundays off. That is, they formalize the problem mathematically and want to find a 6-edge coloring of the 6-regular odd graph . If equals 3, 4 or 8, edge coloring requires exactly colors, but if equals 5, 6 or 7 only colors are needed.
Connection with matchings

A matching in a graph is a set of edges , none of which are adjacent . A perfect matching is a matching that contains edges that touch all nodes of the graph, and a maximal matching is a matching that contains as many edges as possible. In the case of edge coloring, the set of edges with a color must not be adjacent so that they form a matching. That is, a valid edge coloring is the same as a division of the graph into disjoint matchings.
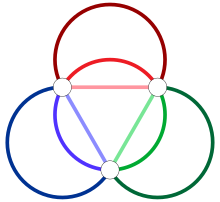
When the size of a maximum matching in a given graph is small, many matchings are required to cover all edges of the graph. In other words, this means that every edge coloring of the graph must use at least different colors if a graph has a total of edges and at most edges can belong to a maximum match. For example, the 3- regular planar graph shown in the figure has 16 nodes and edges. There can be no perfect matching in this graph . When the middle node is included in a matching, the remaining nodes can be grouped into three different connected components of four, five, and five nodes, and the components with an odd number of nodes cannot contain perfect matchings. However, the graph has maximal matchings with edges. Therefore, the number of colors needed to color the edges of the graph is at least , and because the number of colors must be an integer, it is at least 4 colors.
For a regular graph with knot degree that does not have a perfect matching , this lower bound can be used to show that at least colors are needed. This is especially true for a regular graph with an odd number of nodes, for example the odd complete graphs . For such graphs itself must be even according to the handshake lemma . However, the inequality does not fully explain the chromatic index of every regular graph, because there are regular graphs that have perfect matchings but are not k-edge colorable. For example, the Petersen graph is regular with edges and has a perfect matching with edges, but it has no edge coloring with colors.
Duality for corner coloring
The determination of an edge coloring is dual to the determination of a node coloring in such a way that an edge coloring of a graph is exactly eis a node coloring of the edge graph . It follows that . The edge chromatic number of a graph is therefore exactly the chromatic number of the edge graph. Despite this close relationshipThe problems are differently difficult to solve and the available estimates differ significantly.
Generalizations
A major generalization of the edgescoloring is the term for list coloring . Here a list of available colors is provided for each edge (or each node)and the graph should now get a valid edge coloring from these lists. There is also total coloring , in which both nodes and edges are to be colored.
literature
- Reinhard Diestel : graph theory . 4th edition. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (354 pages, online version ).
Web links
Individual evidence
- ↑ a b Alexander Soifer: The Mathematical Coloring Book . In: Springer-Verlag . 2008.
- ^ Norman Biggs: An edge-coloring problem . In: American Mathematical Monthly . 79, No. 9, 1972, pp. 1018-1020. doi : 10.2307 / 2318076 .