Sphere (descriptive geometry)

Sphere outline in central projection: two towers, solution in architect arrangement, details: see p. below

The sphere plays an important role in technology and architecture and, alongside cylinders and cones, is one of the classic objects that are dealt with graphically in descriptive geometry . In Descriptive Geometry, a sphere is always represented by its outline (see outline construction ). A distinction is made between the true outline and the apparent outline . The true outline consists of the points on the surface of the sphere where projection rays are tangents. In the case of a central projection, it is always assumed that the projection center (eye point) is never located within the sphere.

The true shape of a sphere is

with parallel projection a great circle of the sphere (i.e. the center of the circle is equal to the center of the sphere),
with central projection a small circle of the sphere (i.e. the center of the circle never coincides with the center of the sphere).

The projection of the true outline is called the apparent outline. The shape of this apparent outline strongly depends on the type of projection.

The apparent shape of a sphere is

with vertical parallel projection a circle with the radius of the sphere,
an ellipse in the case of an oblique parallel projection,
in the case of central projection an ellipse or (in special cases) a circle (see below) under the usual condition that the sphere is in front of the plane of disappearance (otherwise part of the sphere would be behind the viewer).

For the sake of simplicity, outline always means the apparent outline below.

Parallel projection of a sphere

Sphere: outline with oblique parallel projection

Sphere: outline at bird's eye view, principle

Sphere with perpendicular parallel projection

With perpendicular parallel projection (see orthogonal axonometry ) a sphere always appears as a circle with the radius of the sphere. So you only have to construct the image of the center of the sphere and draw a circle with the radius of the sphere. ${\ displaystyle {\ overline {M}}}$ ${\ displaystyle {\ overline {M}}}$

Sphere in engineering axonometry and isometry

Since the Ingenieuraxonometrie and the standard isometric scaled vertical parallel projections are, must at a Ingenieuraxonometrie the ball radius by a factor at a Standardisometrie by the factor are multiplied. ${\ displaystyle 1 {,} 06}$ ${\ displaystyle 1 {,} 225}$

Sphere: outline in a cavalier perspective, principle
Sphere: domed building from a gentleman's perspective

Sphere with oblique parallel projection

In the case of an oblique parallel projection, the image of a sphere is an ellipse. To determine its center point and the axes, we consider the projection of a sphere in a two-panel projection (see picture). You can see that the projection rays create a cylinder when reproducing the true outline of the sphere, the intersection of which with the plan is the outline ellipse. That the intersection of a cylinder with a plane not parallel to the axis is an ellipse can be made clear with the help of Dandelin's spheres . ${\ displaystyle w}$

The center of the outline ellipse is the image of the center of the sphere,
the semi-minor axis is the radius of the sphere and ${\ displaystyle b}$
the direction of the main axis is the direction of the projection rays in the plan (illustration of the oblique parallel projection).

To find the length of the semi-major axis, one uses that

the focal points of the outline ellipse are the images of the points of the spherical diameter perpendicular to the image table (here floor plan). This gives the distance between the focal points and the center. To justify this, think of the sphere sliding downwards along the projection rays. The ball will first touch the ground plan level with its lowest point at the point as the first Dandelin sphere and when sliding on the ground plan level with the point as the second Dandelin sphere. ${\ displaystyle F_ {1}, F_ {2}}$ ${\ displaystyle P_ {1}, P_ {2}}$ ${\ displaystyle e}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle P_ {1}}$ ${\ displaystyle F_ {1}}$

The semi-axis length results from the relationship (see picture) and the ellipse can be drawn (e.g. with the log curvature circle method). ${\ displaystyle a ^ {2} = b ^ {2} + e ^ {2}}$ ${\ displaystyle a}$

Ball at bird's eye view

A bird's eye view is an oblique parallel projection onto a horizontal picture board. Axonometrically this means: the x- and y-coordinates can be used unabridged and the z-coordinates are reduced by multiplication with a shortening factor . To depict a sphere (for the sake of simplicity) with its center at the origin, one determines ${\ displaystyle v_ {z}}$

the image of the center of the sphere (here the zero point),
the image of a point of the perpendicular sphere diameter and obtains , ${\ displaystyle F_ {1}}$ ${\ displaystyle e}$
the major semi-axis (see picture: the direction of projection in the image table is the direction of the image on the z-axis).

Ball at a gentleman's perspective

In this case, parallel beams are used to project obliquely onto a vertical image panel. In the example the table is the yz-plane. This means axonometric: the y and z coordinates are taken over unchanged and the x coordinates are shortened by multiplication with a factor . The direction of projection in the image table is determined here by the image of the x-axis. The outline ellipse is constructed in the same way as a bird's eye view. A focal point results here from the projection of a point of the sphere diameter perpendicular to the yz plane. ${\ displaystyle v_ {x}}$

Central projection of a sphere: examples

Central projection of a sphere

Sphere: outline at central projection, Dandelin spheres

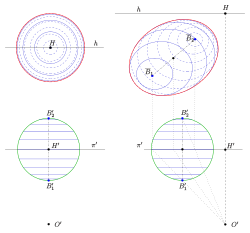
The (apparent) outline of a sphere in central projection can be imagined as the intersection of the straight cone, which is created by the sphere and the visual rays that touch it, with the image board. Since a plane that does not go through the apex of the cone intersects a cone in a non-degenerate conic section, an ellipse, hyperbola or parabola can appear as images of the sphere. We only want to consider the "usual" case that the sphere lies in front of the vanishing plane. This means that the sphere will always appear here as an ellipse or circle. The outline ellipse as an image of the true outline circle is not as easy to construct as with parallel projection, there

with central projection i. A. The center of a circle is not the center of the image ellipse (see Ellipse (Descriptive Geometry) ).

Only if the center of the sphere lies on the straight line through the eye point and the main point, the outline is again a circle and its center is the main point. So here we will first construct the two focal points of the image ellipse. Its center is then the center of the ellipse and the main vertices lie on its connecting line. ${\ displaystyle F_ {1}, F_ {2}}$ ${\ displaystyle M_ {e}}$

In order to determine the archetypes of the focal points, we imagine the following: We let the ball slide along within the cone created with the lines of sight and inflate it at the same time so that it always touches the cone from the inside in a circle until the inflated ball touches the panel at the point . In this position, the inflated sphere is the first Dandelin sphere of the image ellipse. By moving and inflating it further, the ball touches the panel at the point and becomes the second Dandelin ball. In this process, the diameter perpendicular to the picture board merges into the perpendicular in or onto the picture board. ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {2}}$ ${\ displaystyle P_ {1}, P_ {2}}$ ${\ displaystyle F_ {1}}$ ${\ displaystyle F_ {2}}$

Construction steps (see example: template and solution):

Draw the sphere diameter perpendicular to the illustration in the plan. ${\ displaystyle P_ {1}, P_ {2}}$
Mapping (according to the architect's arrangement ) of the two points results in the focal points . The straight line through is a depth line and has the main point as the vanishing point. ${\ displaystyle P_ {1}, P_ {2}}$ ${\ displaystyle {\ overline {P}} _ {1}, {\ overline {P}} _ {2}}$ ${\ displaystyle P_ {1}, P_ {2}}$ ${\ displaystyle H}$
Center of is the center of the ellipse. ${\ displaystyle {\ overline {M}} _ {e}}$ ${\ displaystyle {\ overline {P}} _ {1}, {\ overline {P}} _ {2}}$
Construction of the archetype of . ${\ displaystyle M_ {e}}$ ${\ displaystyle {\ overline {M}} _ {e}}$
The illustration of the spherical circle with the center parallel to the picture table results in the small semi-axis of the ellipse. ${\ displaystyle M_ {e}}$ ${\ displaystyle b}$
The major semi-axis results from the relationship . ${\ displaystyle a ^ {2} = e ^ {2} + b ^ {2}}$
Draw the image ellipse (e.g. using the circle of curvature method).

Sphere: outline for central projection, example, template (left) and solution

Sphere: central projection of two spherical towers, solution

The last picture shows the solution of the first example: central projection of two spherical towers. The image of the ball on the left appears distorted. The reason: Part of the sphere is no longer in the cone of vision (see circle of vision ). In order to reduce or even avoid such distortions, the distance must be increased until the object to be imaged lies within the cone of vision. Then the outline ellipse becomes "more like a circle". This means that their semi-axes are not very different, which was avoided in the example in order to emphasize the elliptical character of the ball outline. ${\ displaystyle a, b}$

literature

Fucke, Kirch, Nickel: Descriptive Geometry. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4 , p. 164.
Graf, Barner: Descriptive Geometry. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9 , pp. 128, 290.
C. Leopold: Geometric Basics of Architectural Representation. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X , p. 133.

Web links

Descriptive geometry for architects (PDF; 1.5 MB). Script (Uni Darmstadt), p. 145.