Inellipse

Example of an ellipse

An inellipse is an ellipse in geometry that touches the sides of a given triangle . The simplest example is the inscribed circle . Other important examples are the Steiner Inellipse , which touches the sides of the triangle in the middle, the Mandart Inellipse and the Brocard Inellipse . They play a role in triangle geometry . If the ellipse is not restricted by special requirements, there are infinitely many inellipses for a triangle.

Since a non-degenerate conic section is uniquely determined by 5 defining pieces (points, tangents), the contact points for an inellipse of a triangle can only be specified on two sides. The point of contact on the 3rd side is then clearly defined.

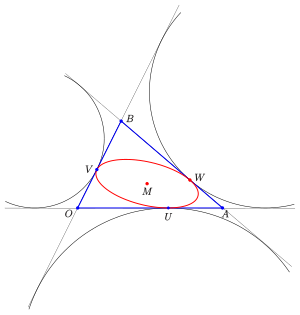
Parametric representations, center point, conjugate radius

An ellipse is clearly defined by the triangle and the specification of the two contact points . (M = center of the ellipse) ${\displaystyle U,V}$

The inellipse of the triangle with the corner points

${\displaystyle O=(0,0),\;A=(a_{1},a_{2}),\;B=(b_{1},b_{2})}$

and the two points of contact

${\displaystyle U=(u_{1},u_{2}),\;V=(v_{1},v_{2})}$

on the side or can be through the rational parametric representation ${\displaystyle OA}$ ${\displaystyle OB}$

• ${\displaystyle \left({\frac {4u_{1}\xi ^{2}+v_{1}ab}{4\xi ^{2}+4\xi +ab}},{\frac {4u_{2}\xi ^{2}+v_{2}ab}{4\xi ^{2}+4\xi +ab}}\right)\ ,\ -\infty <\xi <\infty \ ,}$

describe. The contact points are determined by the specifications as follows: ${\displaystyle a,b}$

${\displaystyle a={\frac {1}{s-1}},\ u_{i}=sa_{i},\quad b={\frac {1}{t-1}},\ v_{i}=ta_{i}\;,\ 0<s,t<1\;.}$

The 3rd touch point is

${\displaystyle W=\left({\frac {u_{1}a+v_{1}b}{a+b+2}}\;,\;{\frac {u_{2}a+v_{2}b}{a+b+2}}\right)\;.}$

The center of the inellipse is

${\displaystyle M={\frac {ab}{ab-1}}\left({\frac {u_{1}+v_{1}}{2}},{\frac {u_{2}+v_{2}}{2}}\right)\;.}$

The vectors

${\displaystyle {\vec {f}}_{1}={\frac {1}{2}}{\frac {\sqrt {ab}}{ab-1}}\;(u_{1}+v_{1},u_{2}+v_{2})}$

${\displaystyle {\vec {f}}_{2}={\frac {1}{2}}{\sqrt {\frac {ab}{ab-1}}}\;(u_{1}-v_{1},u_{2}-v_{2})\;}$

are two conjugate radiuses and the inellipse thus has the further (usual) parametric representation

• ${\displaystyle {\vec {x}}={\vec {OM}}+{\vec {f}}_{1}\cos \varphi +{\vec {f}}_{2}\sin \varphi \;.}$

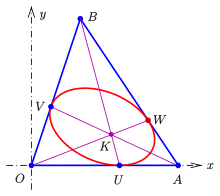
Brianchon point of an ellipse of a triangle

The Brianchon point of the inellipse (common point of the straight line ) is ${\displaystyle K}$ ${\displaystyle {\overline {AV}},{\overline {BU}},{\overline {OW}}}$

${\displaystyle K:\left({\frac {u_{1}a+v_{1}b}{a+b+1}}\;,\;{\frac {u_{2}a+v_{2}b}{a+b+1}}\right)\ .}$

With the help of the numbers , the two points of contact can be easily varied. The barriers to ensure that the contact points really lie on the two sides of the triangle. They deliver for the barriers . ${\displaystyle s,t}$ ${\displaystyle U,V}$ ${\displaystyle s,t}$ ${\displaystyle a,b}$ ${\displaystyle -\infty <a,b<-1}$

Note that here are not the semi-axes of the ellipse or sides of the triangle, but parameters that define the relationship between the contact points and the corner points ! ${\displaystyle a,b}$ ${\displaystyle U,V}$ ${\displaystyle A,B}$

Examples

Mandart inellipse

Steiner inellipse

For the points of contact are the middle of the sides and the inellipse is the Steiner inellipse (center is the center of gravity). ${\displaystyle s=t={\tfrac {1}{2}}}$ ${\displaystyle U,V,W}$

Inscribed circle

For is the inscribed circle of the triangle with the center ${\displaystyle s={\tfrac {|OA|+|OB|-|AB|}{2|OA|}},\;t={\tfrac {|OA|+|OB|-|AB|}{2|OB|}}}$

${\displaystyle {\vec {OM}}={\tfrac {|OB|{\vec {OA}}+|OA|{\vec {OB}}}{|OA|+|OB|+|AB|}}\;.}$

Mandart inellipse

For you get the Mandart ellipse of the triangle. She touches the sides in the contact points of the circles . Your center point is the center point of the triangle. ${\displaystyle s={\tfrac {|OA|-|OB|+|AB|}{2|OA|}},\;t={\tfrac {-|OA|+|OB|+|AB|}{2|OB|}}}$

Brocard inellipse

Brocard inellipse

For you get the Brocard inellipse . It is uniquely determined by the specification of its Brianchon point in trilinear coordinates . ${\displaystyle \ s={\tfrac {|OB|^{2}}{|OB|^{2}+|AB|^{2}}}\;,\quad t={\tfrac {|OA|^{2}}{|OA|^{2}+|AB|^{2}}}\;}$ ${\displaystyle \ K:(|OB|:|OA|:|AB|)\ }$

Derivations

Determination of the inellipse by solving the problem for a hyperbola in the plane and then transforming the solution into the xy plane. is the center of the sought ellipse and two conjugate diameters. Corresponding points have been designated with the same letters in both illustrations. is the distance line of the xy representation. ${\displaystyle \xi -\eta -}$
${\displaystyle M}$ ${\displaystyle D_{1}D_{2},\;E_{1}E_{2}}$
${\displaystyle g_{\infty }}$

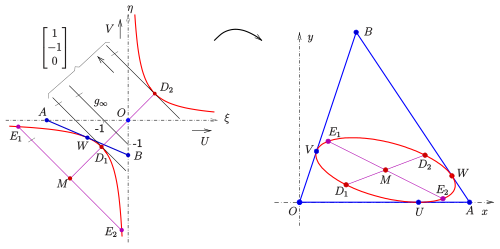
New coordinates

To prove this, one looks at the task projectively and introduces suitable new inhomogeneous - -coordinates in such a way that the desired conic section becomes the hyperbola with the coordinate axes as asymptotes and becomes the far points of the coordinate axes. The triangle points are described in the new coordinates (with square brackets) and the straight line for them has the equation . ( The reverse figure below shows that the ones used here are actually identical to those in the statement of the theorem.) We are now looking for a hyperbola with the coordinate axes as asymptotes that touches the straight line . It is easy to calculate that this is the case for the hyperbola with the equation . It touches the straight line at the point . ${\displaystyle \xi }$ ${\displaystyle \eta }$ ${\displaystyle U,V}$ ${\displaystyle A=(a_{1},a_{2}),\;B=(b_{1},b_{2})}$ ${\displaystyle A=[a,0],B=[0,b]}$ ${\displaystyle {\frac {\xi }{a}}+{\frac {\eta }{b}}=1}$ ${\displaystyle a,b}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle \eta ={\frac {ab}{4\xi }}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle W=[{\tfrac {a}{2}},{\tfrac {b}{2}}]}$

Coordinate transformation

The re-image of the solution found is homogeneously represented by the matrix

${\displaystyle {\begin{bmatrix}u_{1}&v_{1}&0\\u_{2}&v_{2}&0\\1&1&1\end{bmatrix}}\quad }$ described.

One point will be on ${\displaystyle [x_{1},x_{2},x_{3}]}$

${\displaystyle {\begin{bmatrix}u_{1}&v_{1}&0\\u_{2}&v_{2}&0\\1&1&1\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}}={\begin{pmatrix}u_{1}x_{1}+v_{1}x_{2}\\u_{2}x_{1}+v_{2}x_{2}\\x_{1}+x_{2}+x_{3}\end{pmatrix}}\rightarrow \left({\frac {u_{1}x_{1}+v_{1}x_{2}}{x_{1}+x_{2}+x_{3}}}\;,\;{\frac {u_{2}x_{1}+v_{2}x_{2}}{x_{1}+x_{2}+x_{3}}}\right)\quad }$pictured if is. A point on the - plane is represented by the column vector (see homogeneous coordinates ). The representation has a distant point . ${\displaystyle x_{1}+x_{2}+x_{3}\neq 0}$ ${\displaystyle [\xi ,\eta ]}$ ${\displaystyle \xi }$ ${\displaystyle \eta }$ ${\displaystyle [\xi ,\eta ,1]^{T}}$ ${\displaystyle [\cdots ,\cdots ,0]^{T}}$

Coordinate transformation of essential points

${\displaystyle U:\ [1,0,0]^{T}\ \rightarrow \ (u_{1},u_{2})\ ,\quad V:\ [0,1,0]^{T}\ \rightarrow \ (v_{1},v_{2})\ ,}$

${\displaystyle O:\ [0,0]\ \rightarrow \ (0,0)\ ,\quad A:\ [a,0]\rightarrow \ (a_{1},a_{2})\ ,\quad B:\ [0,b]\rightarrow \ (b_{1},b_{2})\ ,}$

(Note that: is.) ${\displaystyle \ a={\tfrac {1}{s-1}},\ u_{i}=sa_{i},\quad b={\tfrac {1}{t-1}},\ v_{i}=ta_{i}\;}$

${\displaystyle g_{\infty }:\xi +\eta +1=0\ }$is the equation of the distance line of the xy plane, your distance point is . ${\displaystyle [1,-1,0]^{T}}$

${\displaystyle [1,-1,0]^{T}\ \rightarrow \ (u_{1}-v_{1},u_{2}-v_{2},0)^{T}}$

The far point of in the - plane therefore changes into a far point of the xy plane, the far point of the straight line . This means: The two in - coordinates to parallel tangents of the hyperbola are also parallel in the xy coordinates. The points of contact of these tangents are: ${\displaystyle g_{\infty }}$ ${\displaystyle \xi }$ ${\displaystyle \eta }$ ${\displaystyle {\overline {UV}}}$ ${\displaystyle \xi }$ ${\displaystyle \eta }$ ${\displaystyle g_{\infty }}$

${\displaystyle D_{i}:[{\frac {\pm {\sqrt {ab}}}{2}},{\frac {\pm {\sqrt {ab}}}{2}}]\ \rightarrow \ {\frac {1}{2}}{\frac {\pm {\sqrt {ab}}}{1\pm {\sqrt {ab}}}}\;(u_{1}+v_{1},u_{2}+v_{2}),\;}$

Since the ellipse tangents are parallel in the points in the xy plane , a diameter of the ellipse, i.e. H. the midpoint of the line is the midpoint of the ellipse: ${\displaystyle D_{1},D_{2}}$ ${\displaystyle D_{1}D_{2}}$ ${\displaystyle D_{1}D_{2}}$ ${\displaystyle M}$

${\displaystyle M:\ {\frac {1}{2}}{\frac {ab}{ab-1}}\left(u_{1}+v_{1},u_{2}+v_{2}\right)\;}$

It is easy to check that the - representation ${\displaystyle M}$ ${\displaystyle \xi }$ ${\displaystyle \eta }$

${\displaystyle \ M:\;[{\frac {-ab}{2}},{\frac {-ab}{2}}]\ }$

Has. In order to find the elliptical diameter to be conjugated, one must determine the intersection points of the straight line parallel to the tangents through (it has the equation ) with the hyperbola in the - plane . It turns out . And in xy coordinates ${\displaystyle D_{1}D_{2}}$ ${\displaystyle \xi }$ ${\displaystyle \eta }$ ${\displaystyle E_{1},E_{2}}$ ${\displaystyle M}$ ${\displaystyle \xi +\eta +ab=0}$ ${\displaystyle E_{i}:\ [{\tfrac {-ab\pm {\sqrt {ab(ab-1)}}}{2}},{\tfrac {-ab\mp {\sqrt {ab(ab-1)}}}{2}}]\ }$

${\displaystyle \ E_{i}={\frac {1}{2}}{\frac {ab}{ab-1}}\left(u_{1}+v_{1},u_{2}+v_{2}\right)\pm {\frac {1}{2}}{\frac {\sqrt {ab(ab-1)}}{ab-1}}\left(u_{1}-v_{1},u_{2}-v_{2}\right)\;,}$

Two vector conjugate radiuses can be determined from the two conjugate diameters : ${\displaystyle D_{1}D_{2},E_{1}E_{2}}$ ${\displaystyle {\vec {f}}_{1},{\vec {f}}_{2}}$

${\displaystyle {\vec {f}}_{1}={\vec {MD_{1}}}={\frac {1}{2}}{\frac {\sqrt {ab}}{ab-1}}\;(u_{1}+v_{1},u_{2}+v_{2})}$

${\displaystyle {\vec {f}}_{2}={\vec {ME_{1}}}={\frac {1}{2}}{\sqrt {\frac {ab}{ab-1}}}\;(u_{1}-v_{1},u_{2}-v_{2})\;.}$

This results in a trigonometric parameter representation of the inellipse:

${\displaystyle {\vec {x}}={\vec {OM}}+{\vec {f}}_{1}\cos \varphi +{\vec {f}}_{2}\sin \varphi \;.}$

From this, as with the Steiner ellipse, the semiaxes, eccentricity, the surface area, the vertex and an equation in xy coordinates of the inellipse can be calculated.

The following applies to the contact point of the side : ${\displaystyle W}$ ${\displaystyle AB}$

${\displaystyle W:\ [{\frac {a}{2}},{\frac {b}{2}}]\ \rightarrow \ \left({\frac {u_{1}a+v_{1}b}{a+b+2}}\;,\;{\frac {u_{2}a+v_{2}b}{a+b+2}}\right)\;.}$

The Brianchon point of the inellipse is the common point of the three straight lines . First calculate in the - -plane as the intersection of the three straight lines: and transform the intersection into the xy-plane. It turns out ${\displaystyle K}$ ${\displaystyle {\overline {AV}},{\overline {BU}},{\overline {OW}}}$ ${\displaystyle K}$ ${\displaystyle \xi }$ ${\displaystyle \eta }$ ${\displaystyle \xi =a\;,\;\eta =b\;,\;a\eta -b\xi =0}$

${\displaystyle K:\ [a,b]\ \rightarrow \ \left({\frac {u_{1}a+v_{1}b}{a+b+1}}\;,\;{\frac {u_{2}a+v_{2}b}{a+b+1}}\right)\ .}$

The point-by-point transformation of the hyperbola provides a rational parametric representation of the inellipse: ${\displaystyle \ \eta ={\frac {ab}{4\xi }}}$

${\displaystyle [\xi ,{\frac {ab}{4\xi }}]\ \rightarrow \ \left({\frac {4u_{1}\xi ^{2}+v_{1}ab}{4\xi ^{2}+4\xi +ab}},{\frac {4u_{2}\xi ^{2}+v_{2}ab}{4\xi ^{2}+4\xi +ab}}\right)\ ,\ -\infty <\xi <\infty \ .}$

Inscribed circle

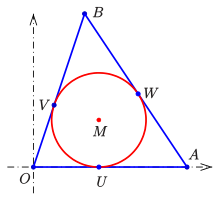
Inscribed circle of a triangle

For the inscribed circle applies and thus ${\displaystyle |OU|=|OV|}$

(1) Furthermore applies in this case ${\displaystyle \;s|OA|=t|OB|\;.\ }$

(2) . (see picture) ${\displaystyle \;(1-s)|OA|+(1-t)|OB|=|AB|}$

If you solve both equations for , you get ${\displaystyle s,t}$

(3) ${\displaystyle \;s={\tfrac {|OA|+|OB|-|AB|}{2|OA|}},\;t={\tfrac {|OA|+|OB|-|AB|}{2|OB|}}\;.}$

To determine the center point, one first calculates with the help of (1) and (3)

${\displaystyle 1-1/ab=1-(s-1)(t-1)=-st+s+t=\cdots ={\tfrac {s}{2(|OB|}}(|OA|+|OB|+|AB|)\;.}$

So is

${\displaystyle {\vec {OM}}={\tfrac {|OB|}{s(|OA|+|OB|+|AB|)}}\;(s{\vec {OA}}+t{\vec {OB}})=\cdots ={\tfrac {|OB|{\vec {OA}}+|OA|{\vec {OB}}}{|OA|+|OB|+|AB|}}\;.}$

Mandart inellipse

The parameters for the Mandart ellipse result from the information for the distances between the contact points of the circles (see circle ) and the corners. ${\displaystyle s,t}$

Brocard inellipse

The Brocard inellipse is determined by the specification of its Brianchon point . It has the simple representation in trilinear coordinates . If you convert the trilinear coordinates into the representation suitable here , you get . If, on the other hand, the parameters of an inellipse are given, the above formula for that is. If one sets the expressions for each equal and solves for , the result is ${\displaystyle K}$ ${\displaystyle \ K:(|OB|:|OA|:|AB|)\ }$ ${\displaystyle \ K:k_{1}{\vec {OA}}+k_{2}{\vec {OB}}\ }$ ${\displaystyle \ k_{1}={\tfrac {|OB|^{2}}{|OB|^{2}+|OA|^{2}+|AB|^{2}}},\;k_{2}={\tfrac {|OA|^{2}}{|OB|^{2}+|OA|^{2}+|AB|^{2}}}\ }$ ${\displaystyle s,t}$ ${\displaystyle K}$ ${\displaystyle \ k_{1}={\tfrac {s(t-1)}{st-1}},\;k_{2}={\tfrac {t(s-1)}{st-1}}\ }$ ${\displaystyle k_{1},k_{2}}$ ${\displaystyle s,t}$

${\displaystyle s={\tfrac {|OB|^{2}}{|OB|^{2}+|AB|^{2}}}\;,\quad t={\tfrac {|OA|^{2}}{|OA|^{2}+|AB|^{2}}}\;.}$

Inellipse with maximum area

• The Steiner inellipse has the largest area of ​​all inellipses of a triangle.

proof

From a theorem of Apollonios it follows that the area of ​​an ellipse is equal to the conjugate radius ${\displaystyle {\vec {f}}_{1},{\vec {f}}_{2}}$

${\displaystyle F=\pi \left|\det({\vec {f}}_{1},{\vec {f}}_{2})\right|\quad }$is (see article Steiner-Ellipse ).

For the inellipse with the parameters (see above) ${\displaystyle s,t}$

${\displaystyle \det({\vec {f}}_{1},{\vec {f}}_{2})={\frac {1}{4}}{\frac {ab}{(ab-1)^{3/2}}}\det(s{\vec {a}}+t{\vec {b}},s{\vec {a}}-t{\vec {b}})}$

${\displaystyle ={\frac {1}{2}}{\frac {s{\sqrt {s-1}}\;t{\sqrt {t-1}}}{(1-(s-1)(t-1))^{3/2}}}\det({\vec {b}},{\vec {a}})\;.}$

(It is . Note the rules for determinants!) To avoid the roots in the calculation, it is sufficient to determine the extreme points of the function : ${\displaystyle {\vec {a}}=(a_{1},a_{2}),\;{\vec {b}}=(b_{1},b_{2}),\;{\vec {u}}=(u_{1},u_{2}),{\vec {v}}=(v_{1},v_{2}),\;{\vec {u}}=s{\vec {a}},\;{\vec {v}}=t{\vec {b}}}$
${\displaystyle G(s,t)={\tfrac {s^{2}(s-1)\;t^{2}(t-1)}{(1-(s-1)(t-1))^{3}}}}$

${\displaystyle G_{s}=0\ \rightarrow \ 3s-2+2(s-1)(t-1)=0\;.}$

Because of swapping s and t one gets: ${\displaystyle G(s,t)=G(t,s)}$

${\displaystyle G_{t}=0\ \rightarrow \ 3t-2+2(s-1)(t-1)=0\;.}$

Solving the two equations for s and t yields

${\displaystyle s=t={\frac {1}{2}}\;,\quad }$d. H.:

The Steiner inellipse is the inellipse with a maximum area.

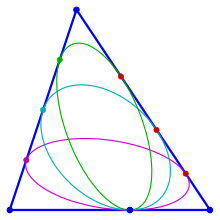
3 touching ellipses in a triangle

Web links

• Darij Grinberg: About a few sentences and exercises from triangular geometry
• Circumconic at MathWorld
• Inconic at MathWorld

Individual evidence

1. ↑ Imre Juhász: Control point based representation of inellipses of triangles , Annales Mathematicae et Informaticae 40 (2012) pp. 37-46, p. 44