Steiner ellipse

The Steiner ellipse of an isosceles triangle . The three lines within the triangle are bisectors . These intersect in the geometric center of gravity of the triangle, which coincides with the center of the Steiner ellipse.

In geometry , the Steiner ellipse of a triangle ( also known as the Steiner umellipse to distinguish it from the Steiner inellipse ) is the uniquely determined ellipse that goes through the corners of the triangle and whose center is the center of gravity of the triangle. The ellipse named after Jakob Steiner is an example of a circumscribed conic section . For comparison: the perimeter of a triangle is also such a conic section that runs through the corners; but the circumcenter does not coincide with the center of gravity - except when the triangle is equilateral .

The area of ​​the Steiner ellipse is equal to the area of ​​the triangle and consequently four times the size of the Steiner inellipse. The Steiner ellipse has the smallest area of ​​all the ellipses circumscribed by the triangle. ${\displaystyle {\tfrac {4\pi }{3{\sqrt {3}}}}}$

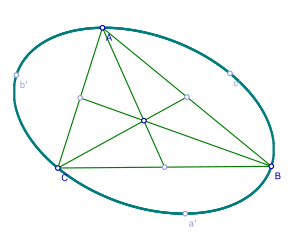
Property of a Steiner ellipse

Steiner ellipse of an equilateral (left) and isosceles triangle

• A Steiner ellipse is the only ellipse that has the center of gravity of a triangle and runs through the corners of the triangle. The area of ​​the Steiner ellipse is equal to the area of ​​the triangle. ${\displaystyle S}$ ${\displaystyle ABC}$ ${\displaystyle {\tfrac {4\pi }{3{\sqrt {3}}}}}$

proof

A) With an equilateral triangle, the ellipse is obviously the perimeter. It is the only ellipse that meets the requirements. Because since the center of the ellipse is, the three at mirrored corners must also lie on the ellipse. This is the case for the perimeter. Since a conic section is clearly defined by 5 points, the circle is the only ellipse with the required property. ${\displaystyle S}$ ${\displaystyle S}$

B) Since any triangle can be viewed as an affine image of an equilateral triangle, a circle in an affine mapping into an ellipse and the center of gravity of a triangle into the center of gravity of the image triangle, the property (exactly one umellipse with center in the center of gravity) applies to all triangles.

The area of ​​the perimeter of an equilateral triangle is equal to -fold the area of ​​the triangle. In the case of an affine mapping, area ratios remain unchanged. So this statement about the area ratio also applies to any triangle and its Steiner ellipse. ${\displaystyle {\tfrac {4\pi }{3{\sqrt {3}}}}}$

Construction of conjugate radiuses

To be able to draw an ellipse, you need at least two conjugate radiuses . Then let yourself

• either determine the vertex with the help of a Rytz construction and draw the ellipse with an elliptical compass
• or draw the ellipse as a parameterized curve with a computer program .

The vertices and semi-axes and therefore also the eccentricity can also be determined mathematically .

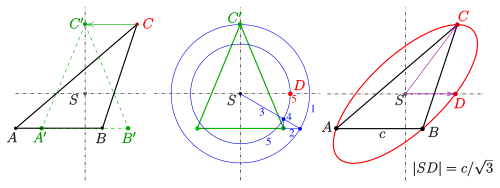
Construction steps of a drawing determination of the Steiner ellipse:
1) Shear the triangle to an isosceles
2) Determination of the point (steps 1–5) 3) Draw the ellipse with the help of the conjugate radius ${\displaystyle D}$
${\displaystyle SC,SD}$

Let it be a triangle and its center of gravity. If you lay to the side through a parallel and lead the triangle through a shear into an isosceles triangle (see picture), then there is a vertex of the Steiner ellipse of the triangle . Another vertex of this ellipse rests on , because it is perpendicular to (for reasons of symmetry). This vertex can be calculated from the data (ellipse with center through and , ) . It results: ${\displaystyle ABC}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle d}$ ${\displaystyle AB}$ ${\displaystyle d}$ ${\displaystyle A'B'C'}$ ${\displaystyle C'}$ ${\displaystyle A'B'C'}$ ${\displaystyle D}$ ${\displaystyle d}$ ${\displaystyle d}$ ${\displaystyle SC'}$ ${\displaystyle S}$ ${\displaystyle C'}$ ${\displaystyle B'}$ ${\displaystyle |A'B'|=c}$

${\displaystyle |SD|={\frac {c}{\sqrt {3}}}}$

Or: The vertex of the umellipse of the isosceles triangle is determined graphically with the help of de la Hire's elliptical construction (see middle picture) . If the shear is reversed, it changes back to and remains fixed as the point of the shear axis. This is a conjugate radius. In general, both are not perpendicular to each other. With the help of this conjugate radius, as described above, the Steiner ellipse can be drawn. ${\displaystyle D}$ ${\displaystyle A'B'C'}$
${\displaystyle C'}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle SD}$ ${\displaystyle SC}$

Parametric plot and equation

Steiner ellipse of a triangle with axes and vertices (magenta)

Given: Triangle Wanted: Parameter representation and equation of the associated Steiner ellipse. ${\displaystyle \ A=(a_{1},a_{2}),\;B=(b_{1},b_{2}),\;C=(c_{1},c_{2})}$

The center of gravity of the triangle is ${\displaystyle \ S=({\tfrac {a_{1}+b_{1}+c_{1}}{3}},{\tfrac {a_{2}+b_{2}+c_{2}}{3}})\ .}$

Parameter representation:

• The following parameter representation of the Steiner ellipse results from the considerations in the previous section:

${\displaystyle {\vec {x}}={\vec {p}}(t)={\overrightarrow {OS}}\;+\;{\overrightarrow {SC}}\;\cos t\;+\;{\frac {1}{\sqrt {3}}}{\overrightarrow {AB}}\;\sin t\;,\quad 0\leq t<2\pi }$

• The 4 vertices of the ellipse are

${\displaystyle {\vec {p}}(t_{0}),\;{\vec {p}}(t_{0}\pm {\frac {\pi }{2}}),\;{\vec {p}}(t_{0}+\pi ),}$

wherein from ${\displaystyle t_{0}}$

${\displaystyle \cot(2t_{0})={\tfrac {{\vec {f}}_{1}^{\,2}-{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f}}_{2}}}\quad }$ With ${\displaystyle \quad {\vec {f}}_{1}={\vec {SC}},\quad {\vec {f}}_{2}={\frac {1}{\sqrt {3}}}{\vec {AB}}}$

results (see ellipse ).

The roles of the points in setting up the parameter display can be interchanged as desired.

Example (see picture): ${\displaystyle A=(-5,-5),B=(0,25),C=(20,0)}$

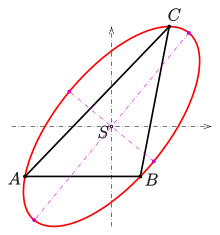
Steiner ellipse as an example for "equation"

Equation:

If the origin is the center of gravity, the equation is the ellipse with the parametric representation ${\displaystyle {\vec {x}}={\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t}$

${\displaystyle (xf_{2y}-yf_{2x})^{2}+(yf_{1x}-xf_{1y})^{2}-(f_{1x}f_{2y}-f_{1y}f_{2x})^{2}=0}$

With

${\displaystyle {\vec {f}}_{i}=(f_{ix},f_{iy})^{T}}$.

Example: For the triangle , the center of gravity is at the zero point and it is ${\displaystyle \quad A=(-{\tfrac {3}{2}}{\sqrt {3}},-{\tfrac {3}{2}}),\ B=({\tfrac {\sqrt {3}}{2}},-{\tfrac {3}{2}}),\ C=({\sqrt {3}},3)\quad }$

${\displaystyle {\vec {f}}_{1}=({\sqrt {3}},3)^{T},\ {\vec {f}}_{2}=(2,0)^{T}}$.

The equation of the Steiner ellipse is:

${\displaystyle 9x^{2}+7y^{2}-6{\sqrt {3}}xy-36=0}$

Calculation of the semi-axes

If the vertex of the Steiner ellipse has already been determined (see previous section), the semiaxes can be calculated from them. If you are only interested in the semi-axes, the following method leads to your goal faster:

If the semiaxes are the Steiner ellipse, then from Apollonios' theorems about properties of conjugate radiuses of ellipses follows: ${\displaystyle a,b,\;a>b}$

${\displaystyle a^{2}+b^{2}={\vec {SC}}^{2}+{\vec {SD}}^{2}\ ,\quad a\cdot b=\left|\det({\vec {SC}},{\vec {SD}})\right|}$

If the right-hand side is designated with or , the non-linear system of equations (taking into account ) reshapes ${\displaystyle M}$ ${\displaystyle N}$ ${\displaystyle a>b>0}$

${\displaystyle a^{2}+b^{2}=M,\ ab=N\quad \rightarrow \quad a^{2}+2ab+b^{2}=M+2N,\ a^{2}-2ab+b^{2}=M-2N}$

${\displaystyle \rightarrow \quad (a+b)^{2}=M+2N,\ (a-b)^{2}=M-2N\quad \rightarrow \quad a+b={\sqrt {M+2N}},\ a-b={\sqrt {M-2N}}}$

and solving for , and to, one receives for the semi-axes: ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle a={\frac {1}{2}}({\sqrt {M+2N}}+{\sqrt {M-2N}})}$

${\displaystyle b={\frac {1}{2}}({\sqrt {M+2N}}-{\sqrt {M-2N}})}$

In addition:

${\displaystyle M={\vec {SC}}^{2}+{\frac {1}{3}}{\vec {AB}}^{2}}$

${\displaystyle N={\frac {1}{\sqrt {3}}}\left|\det({\vec {SC}},{\vec {AB}})\right|}$

For the linear eccentricity of the Steiner ellipse we get:

${\displaystyle e={\sqrt {a^{2}-b^{2}}}=\dotsb ={\sqrt {\sqrt {M^{2}-4N^{2}}}}}$

The area is:

${\displaystyle F=\pi ab=\pi N={\frac {\pi }{\sqrt {3}}}\left|\det({\vec {SC}},{\vec {AB}})\right|}$

Trilinear and barycentric equation

The equation of the Steiner umellipse in trilinear coordinates is

${\displaystyle vwyz+wuzx+uvxy=0}$,

where denote the side lengths of the triangle. ${\displaystyle u,v,w}$

A particularly simple equation is obtained using barycentric coordinates :

${\displaystyle yz+zx+xy=0}$

Alternative calculation of the semi-axes and focal points

The lengths of the semi-major and minor axes for a triangle with side lengths are ${\displaystyle u,v,w}$

${\displaystyle {\frac {1}{3}}{\sqrt {u^{2}+v^{2}+w^{2}\pm 2Z}}}$

with the abbreviation

${\displaystyle Z:={\sqrt {u^{4}+v^{4}+w^{4}-u^{2}v^{2}-v^{2}w^{2}-w^{2}u^{2}}}.}$

The linear eccentricity is

${\displaystyle {\frac {2}{3}}{\sqrt {Z}}}$.

The focal points of the Steiner ellipse are the so-called Bickart points of the triangle.

Individual evidence

1. ↑ ^{a b c d} Eric W. Weisstein : Steiner Circumellipse . In: MathWorld (English).
2. ↑ CDKG: Computer-assisted Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 65.

literature

• Georg Glaeser, Hellmuth Stachel, Boris Odehnal: The Universe of conics. From the ancient Greeks to 21st century developments. Springer, 2016, ISBN 978-3-662-45449-7 , p. 383.