Maximum Power Point Tracking

In electrical engineering , especially in photovoltaics , the term Maximum Power Point Tracking , MPP Tracking or MPPT (in German about "maximum power point search" ) describes a process in which the electrical load on a solar cell , a solar module or of several solar modules connected in series ("String", German also "Strang") is adjusted so that the greatest possible power can be drawn from the cells . In the case of solar cells, this optimal operating point is not constant, but depends, among other things, on the irradiance , the temperature on the solar module and the type of solar cell.

motivation

Shift of the MPP with changing irradiance as well as current and power in relation to voltage

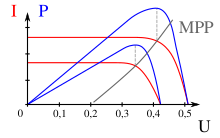
In general, the greatest possible power can be drawn from an electrical source when the product of electrical current I and electrical voltage U has its maximum; this corresponds to the case where the internal resistance of the source is equal to the external load resistance. This operating point is generally considered power adjustment ( English maximum power point , MPP called) and in the adjacent diagram for a solar cell in the black curve MPP displayed. Two exemplary operating states with the respective maximum power P at the intersection are drawn in blue .

In solar cells, the internal resistance or the optimal operating point with maximum power output is not constant, but depends on external factors such as the current irradiance and the temperature of the module. Therefore, the load resistance of the solar module is influenced by an electronically controlled circuit in such a way that the load resistance is continuously adjusted and tracked so that it is almost exactly the same as the current internal resistance of the solar cell and thus the power output of the solar module is always at its maximum under different operating conditions.

In practice, the optimum operating point is set and continuously tracked by an electronic circuit, MPP tracking - in principle a DC / DC converter specially optimized for this task . This is connected on its input side to the solar cell, which is always operated with power adjustment due to the MPP tracking algorithm if the internal resistance changes . On the output side, this maximum gain must be accepted; Usually a battery is charged, the voltage of which changes only slowly, but whose charging current fluctuates according to the power supplied. A direct supply to a consumer is only possible if it can take all the power currently generated. The inverter must always be able to deliver all of its power to a network. It is not possible to connect just one consumer (island grid) without a battery buffer. With solar inverters , the MPP tracking and inverter functions are combined in one device.

Definitions

Current-voltage diagram and representation of the solar module as a diode characteristic

Consideration of an evenly illuminated solar module

The current-voltage diagram, as shown opposite, is typically plotted in such a way that the technical current direction of the measured current points in the reverse direction of the solar cell. In contrast to the classic diode characteristic , the current is applied positively to lighting .

The ratio between the maximum power P _{MPP of} the solar cell at the maximum power point and the product of the open circuit voltage U _L and the short circuit current I _K is called the fill factor FF :

${\displaystyle FF={\frac {P_{\rm {MPP}}}{U_{\rm {L}}\cdot I_{\rm {K}}}}}$

with the function of the open circuit voltage of the solar module:

${\displaystyle U_{\rm {L}}=m\cdot U_{\rm {T}}\cdot \ln \left({\frac {I_{\rm {Ph}}}{I_{\rm {S}}}}+1\right)}$

${\displaystyle m}$ = Diode factor

${\displaystyle U_{\rm {L}}}$ = Open circuit voltage

${\displaystyle I_{\rm {S}}}$ = Saturation current

${\displaystyle U_{\rm {T}}}$= Temperature stress

${\displaystyle I_{\rm {Ph}}}$ = Photocurrent

The photocurrent increases slightly with increasing temperature and is usually neglected in practice. With increasing irradiation of the solar module, the current increases almost proportionally, the output increases. The tension hardly changes. As the temperature rises, the voltage drops slightly because the saturation current, also known as the dark current, increases.

The power, which results from the product of the voltage and the current, decreases with constant irradiation and rising module temperature. Typical values ​​are −0.45% per Kelvin for crystalline silicon solar cells.

Identification features in the current-voltage characteristic

The following properties are determined in the current-voltage characteristic curve as identifying features for successful power adjustment:

• The following applies to performance adjustment in the MPP: ${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} U}}=-{\frac {I}{U}}}$
• In the MPP, the IU characteristic touches the hyperbola with P = Pmpp = const.
• The MPP divides its tangent into two equally long sections.
• The diagonal in the rectangle of the point coordinates is parallel to the tangent.

The identification features are due to the property of the local maximum power (increase dp / dU = 0). They are well suited to determine or check the position of the MPPs in the characteristic curves even without a power axis. They can also be used if the axis scaling is missing.

Consideration of several solar modules connected in series with partial shading

UP characteristic of a partially shaded solar generator. Local and global MPP are marked red and green, respectively.

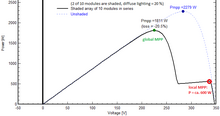
In the adjacent figures, a string of ten solar modules connected in series is shown: The blue dashed curve stands for the case that all modules are evenly irradiated. The black curve stands for the case that two of the ten modules are in the shade and only receive 20% of the irradiation compared to the other modules (through diffuse radiation).

It can be seen that in the shaded case there is no longer just one power maximum, but several. The "global MPP", ie the actual point of maximum power, is marked in green. The "local MPP", ie a local high point on the performance curve, is marked in red.

The cause of this process lies in the bypass diodes that are integrated into the solar modules to protect the individual cells: All modules at the local MPP are operated with the same low current that the shaded modules can still deliver (through diffuse radiation). Only when the voltage is lowered or the current is increased do the bypass diodes of the shaded modules respond and short-circuit these module parts, i.e. bypass them. As a result, the string voltage is lower (the shaded modules are actually "missing" in the string), but the current is significantly higher, which explains the higher power at the global maximum.

UI characteristic of a partially shaded solar generator.

Technical procedures

Shadow management

All of the methods described below search for the MPP in relatively small steps around the current maximum output. This has the advantage that the solar generator is operated very close to the MPP for most of the time (high MPP adaptation efficiency ). The disadvantage is that if the solar generator is partially shaded, the tracker often remains at the local MPP (see above) without finding the way to the global MPP.

That is why most inverter manufacturers have now integrated an additional function that runs through the entire characteristic curve of the solar generator very quickly at regular intervals (usually every 5–10 minutes) in order to search for the global MPP. This function is referred to as shadow management or shading management, in some cases also as a sweeping function , and does not replace continuous MPP tracking.

For the majority of manufacturers, the function is activated at the factory, for others it can be activated in the menu. The yield loss due to the regular running through the characteristic curve (during which the generator is naturally not operated in the MPP) is specified, for example, as <0.2%; the duration for running through the characteristic curve is, for example, 2 seconds.

It should be noted that the input voltage range of the inverter can be a limiting factor: Only if the number of unshaded modules is sufficient to achieve the minimum input voltage of the inverter with these modules alone can the inverter control the global MPP. Therefore, if there is a risk of shading, it is important to install sufficiently long strings. The previous procedure of installing many short strings when there was a risk of shading has been outdated since the introduction of shadow management.

Method of increasing the voltage

Control behavior of a self-made MPP controller on a simulated solar cell. You can see how the controller tracks the load (green curve, pulse width modulation) after the (simulated) solar voltage has changed and when the optimum load (calculated purple curve) is reached, it begins to oscillate.

In the simplest way of searching for the maximum power, the MPP tracker continuously increases the voltage of the solar cell away from zero, which increases the power output. If the power maximum is now reached, the power begins to drop again, which serves as a criterion for terminating the search. This iterative process is carried out periodically by a microprocessor in the MPP tracker, so that operation at the maximum power point is always present even with changing irradiation conditions.

Method of load steps

In the method of the load jumps ( English perturb and observe ) the controller periodically changes the load of the solar cell in small steps (load step) in a certain direction, and then measures the output of the solar cell performance. If the power now measured is higher than the power measured in the previous period, the controller maintains this search direction and performs the next jump in power. If the measured power is less than that of the last measurement period, the controller changes the search direction and now performs load jumps in the opposite direction. In this way, the maximum power is searched for permanently, with the result that the exact point of maximum power is never found, but it is approached up to 1 load step, which is unproblematic if it is small enough. A kind of oscillation arises around the power maximum. In the case of a partially shaded solar generator, the controller remains at the local maximum if it is (by chance) there.

Increasing conductance

Representation of the performance curve with illustration of the conditions

The idea of ​​the method of increasing conductance ( English incremental conductance ) is based on finding the maximum power based on the differential and the specific conductance of the solar cell. The maximum power point is characterized by the fact that the change in the output power in relation to the change in voltage becomes zero. Depending on which side of the power curve the current load point is on, the power-voltage ratio increases or decreases when the load changes, resulting in the following equations:

To the left of the maximum:

${\displaystyle {\frac {dP}{dU}}>0}$

To the right of the maximum:

${\displaystyle {\frac {dP}{dU}}<0}$

At maximum performance:

${\displaystyle {\frac {dP}{dU}}=0}$

By transforming the equations, the following conditions are obtained for the controller, where I and U are the current measured values ​​of the control period and dI , dU are the changes to the previous control period.

To the left of the maximum:

${\displaystyle {\frac {dI}{dU}}>-{\frac {I}{U}}}$

To the right of the maximum:

${\displaystyle {\frac {dI}{dU}}<-{\frac {I}{U}}}$

At maximum performance:

${\displaystyle {\frac {dI}{dU}}=-{\frac {I}{U}}}$

Based on this condition, the controller then changes the load per control cycle step-by-step in the direction in which it approaches the condition of the desired maximum performance. If the system now fulfills this condition, the maximum performance has been found and the search can be ended. If the output power changes due to the lighting intensity of the solar cell, the controller starts the search again.

In the case of a partially shaded solar generator, the controller remains at the local maximum if it is (by chance) there.

Constant tension method

The method of constant voltage ( English Constant voltage ) based on the fact that there is between the open circuit voltage of the solar cell and that voltage at which the solar cell delivers the maximum power that a context. Thus, on the basis of the knowledge of the open circuit voltage, conclusions can be drawn about the load voltage required for drawing the maximum possible power and thus the load. Since the open circuit voltage changes based on different parameters, the controller must measure this periodically during operation. For this purpose, the load is separated from the solar cell for the duration of the voltage measurement. Based on the now measured open circuit voltage, the controller can calculate the optimal load and adjust it when the load and solar cell are reconnected. Since the relationship between open circuit voltage and optimal load voltage is empirically determined in advance and depends on many parameters, the exact maximum performance is not achieved. In the narrower sense, the algorithm is not one that is looking for the actual maximum output and does not work with a partially shaded solar generator.

Method of temperature

With the temperature method, the open circuit voltage is estimated by measuring the temperature on the solar module.

The algorithm calculates the following equation:

${\displaystyle U_{\mathrm {mpp} }(T)=U_{\mathrm {mpp} }(T_{\mathrm {ref} })+u_{V_{\mathrm {mpp} }}(T-T_{\mathrm {ref} })}$

In which:

${\displaystyle U_{\mathrm {mpp} }}$ is the voltage at the MPP operating point;

${\displaystyle T_{\mathrm {ref} }}$ is the reference temperature;

${\displaystyle T}$ is the measured temperature;

${\displaystyle u_{V_{\mathrm {mpp} }}}$ is the temperature coefficient (given by the manufacturer of the module).

Technical implementation

software

In technical implementations of this method, a microcontroller or a digital signal processor usually carries out one of the possible methods. The required measurement data is provided to the processor by an analog-digital converter , with which it can carry out the necessary calculations and forwards the result to a DC voltage converter by means of pulse width modulation .

hardware

Since the load on the solar cell is set on the basis of the load voltage, but the output voltage of the controller should be almost constant, a DC voltage converter is required in order to be able to set the voltage differences and thus the load on the solar cell. In a photovoltaic system, it can happen that the voltage range of the optimal load voltage of the solar cell moves around the voltage of the battery to be charged . Thus, the input voltage of the DC voltage converter can be both greater and less than its output voltage. In order to meet this requirement, a converter topology is required that fulfills this property, such as the inverse converter , the split-pi converter or a converter of a higher order ( Ćuk converter , SEPIC converter , double inverter ).

literature

• Jitendra Prasad: Maximum Power Point tracker solar charge controller (MPPT): MPPT charge controller . LAP LAMBERT Academic Publishing, Saarbrücken 2012, ISBN 978-3-659-18508-3 .

Web links

Commons : Maximum power point tracker  - collection of pictures, videos and audio files

• Project description of an MPPT based on a PIC microcontroller (English) ( MS Word ; 5.1 MB)

Individual evidence

1. ↑ ^{a b} Photovoltaikforum.com: Shadows! Which inverters activate the bypass diodes? In: Photovoltaikforum.com. Retrieved July 18, 2018 . 
2. ↑ SMA: shading management. SMA, accessed July 18, 2018 . 
3. ↑ Video shadow management Kostal- YouTube. Retrieved July 19, 2018 . 
4. ↑ Optimization of perturb and Observe maximum power point tracking method. Archived from the original on December 2, 2012 ; accessed on September 24, 2016 . 
5. ↑ Incremental Conductance Based Maximum Power Point Tracking (MPPT) for Photovoltaic System (PDF; 877 kB)
6. ↑ A MPPT approach based on temperature measurements applied in PV systems - IEEE Conference Publication. Retrieved October 13, 2018 (American English).