Multi-body system
A multi-body system (MBS) is a mechanical system of individual bodies that are coupled to one another by joints or force elements (e.g. springs, dampers) and are under the influence of forces. With the help of kinematics , a branch of mechanics , the movement of the body is formulated mathematically. Although a multi-body system can also be immobile, the term is usually used to describe a system whose parts can move against each other. The investigation of the movement ( dynamics ) of a multi-body system is called multi-body dynamics .
This article gives an overview of some important aspects of multibody systems. However, at the end of the 1990s, many newer sub-areas developed (optimization, sensitivity analysis, robotics, control, automobiles and rail vehicles, etc.) that have not been included in this article.
application areas
Multi-body systems are used to model the movement of (partial) bodies in technical applications:
- robotics
- Vehicle simulation ( driving dynamics , tires , comfort improvement, weight reduction, etc.)
- Simulation of engines , gears , chain drives , belt drives , etc. a.
- Simulation of conveying machines, especially paper machines
- Particle simulation (e.g. sand)
- Biomechanics (movement optimization, prostheses, walking aids, etc.)
- Aviation industry (e.g. take-off / landing maneuvers of aircraft, rotor of a helicopter)
- Simulation of ships and other floating bodies ( hydrodynamic coupling through waves)
- Space research (e.g. satellites )
- Military applications
example
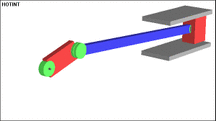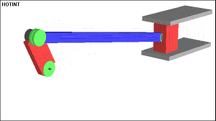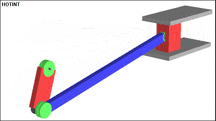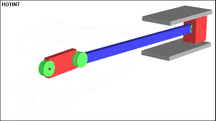
The following figure shows a typical example of a multi-body system. This system will also crank drive ( english slider-crank called). In this example, a rigid body is used for the driven crank, which drives a rotatably mounted connecting rod and finally moves the end mass (concentrated mass). The final mass can only move within the guide. There are 3 swivel joints installed, one between the crank and the inertial system, one between the crank and the connecting rod and one between the connecting rod and the end mass.
Terms
A body is understood to be a solid or flexible body in the mechanical sense (not to be confused with the mathematical body or the human body). A body is, for example, the arm of a robot, the steering wheel of a car, but also the forearm of a human. Joints form flexible connections between bodies. You can z. B. using a joint in the human body or using the example of a joint in a machine or in a car.
Two further terms are of central importance in multi-body dynamics: degree of freedom and constraint.
Degree of freedom
In the sense of a mechanical body, the number of degrees of freedom represents the number of mutually independent possibilities of movement. A rigid body has 6 degrees of freedom for general spatial movement, including 3 degrees of translational freedom and 3 degrees of freedom of rotation. If you only consider the movement of a body (and all of its points) in one plane, this body only has 3 degrees of freedom: 2 degrees of translational freedom and one degree of freedom of rotation.
- example
When looking at a body in space, e.g. B. the computer mouse, the three degrees of translational freedom can be displayed simply by moving left-right, fore-back, up-down. The three degrees of freedom of rotation of the body (the computer mouse) are described by rotation around the axes along which the translation takes place (e.g. around the longitudinal axis of the mouse during translation forwards and backwards).
Constraint
Constraints represent a limitation of the possibilities of movement of bodies. Constraints may also be applied both between two bodies as between a body and a fixed point in space. Contrary to the assumption in the link "Constraints", not only mass points can be constrained. A constraint can also be applied to rotations, speeds (including angular speeds) and accelerations in a multi-body system.
Equations of motion
The motion of the multi-body system is described with the equations of motion, which result from Newton's 2nd axiom and the additional constraints.
The movement of a rigid body system can be expressed as follows:
This formulation is also referred to by the term redundant coordinates . The generalized coordinates represent the degrees of freedom of the bodies not under constraint, is the mass matrix, which can depend on the generalized coordinates, describes the constraints and is the derivation of the constraints according to the generalized coordinates. In this formulation of the equations of motion, the symbol denotes the Lagrange multipliers. If one starts from a single body, the generalized coordinates can be divided into
where describes the translations and describes the rotations.
Quadratic speed vector
The expression represents the quadratic velocity vector, which results from the derivation of the equations from the kinetic energy. This term depends on the selected rotation parameters.
Lagrange multipliers
The Lagrange multipliers are each assigned to a constraint and mostly represent forces or moments that act in the direction of the blocked degree of freedom, but do not do any work.
Constraints and Joints
In the most general language for describing multibody systems, joints are expressed using constraints. As already mentioned, constraints can be used for displacements and rotations as well as for the time derivatives of these quantities.
For the time being, a distinction is made between holonomic and non-holonomic constraints; a more detailed description is given in the section Constraint. For multi-body systems, it is important that common joints such as cylindrical joints, ball joints, prismatic joints etc. are subject to holonomic constraints.
Minimum coordinates
The equations of motion are described with redundant coordinates, which are not independent of each other due to the constraints. Under certain conditions it is possible to overwrite this formulation in a system with non-redundant, i.e. independent coordinates and without constraints. This transformation is generally not possible if the connected bodies have a closed ring (loop) or if they are not simple holonomic joints. Nevertheless, one can switch to a system with the smallest possible number of coordinates by inserting constraints only at certain unavoidable points and using non-redundant coordinates at the other points. One possible type of formulation with minimal coordinates is the so-called recursive formulation.
Commercial software
There are several types of commercial software for multi-body system simulation such as: B. Simcenter Motion from Siemens PLM, RecurDyn from FunctionBay, ThreeParticle / CAE from BECKER 3D, ADAMS from MSC Software or through the company acquisition now part of Hexagon, DS Simulia from Simpack or through the company acquisition now part of Dassault Systems, the Multibody Dynamics Module from COMSOL Multiphysics.
See also
literature
- J. Wittenburg: Dynamics of Systems of Rigid Bodies. Teubner, Stuttgart 1977.
- K. Magnus: Dynamics of multibody systems. Springer Verlag, Berlin 1978.
- PE Nikravesh: Computer-Aided Analysis of Mechanical Systems. , Prentice-Hall, 1988.
- EJ Haug: Computer-Aided Kinematics and Dynamics of Mechanical Systems. Allyn and Bacon, Boston 1989.
- H. Bremer, F. Pfeiffer: Elastic multibody systems. BG Teubner, Stuttgart 1992.
- Ahmed A. Shabana: Dynamics of multibody systems. Cambridge University Press, 3rd edition, 2010, ISBN 978-0521154222
- M. Géradin, A. Cardona: Flexible multibody dynamics - A finite element approach. Wiley, New York 2001.
- J. Gerstmayr: The absolute coordinate formulation with elasto-plastic deformations. In: Journal of Multibody System Dynamics. Vol. 12, 2004, pp. 363-383, doi : 10.1007 / s11044-004-2522-3 .
- Georg Rill, Thomas Schaeffer: Basics and methodology of multi-body simulation: with application examples Vieweg + Teubner Verlag, 2010, ISBN 978-3834808882
- Christoph Woernle: Multi-body systems: An introduction to the kinematics and dynamics of systems of rigid bodies Springer Berlin, 2011, ISBN 978-3642159817
- TJ Jung: Methods of multi-body dynamics simulation as the basis of realistic virtual worlds Online, 2011, available online
Web links
- http://real.uwaterloo.ca/~mbody/ (link collection by John McPhee).
- http://tmech.mechatronik.uni-linz.ac.at/staff (flexible multi-body systems by Johannes Gerstmayr with many animations).








![\ mathbf {q} = \ left [\ mathbf {u} \ quad \ mathbf {\ Psi} \ right] ^ T](https://wikimedia.org/api/rest_v1/media/math/render/svg/c20d6dbee4375da4b6ffc3e0df78921b00d47139)




