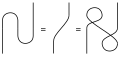Penrose graphic notation

The penrosesche graphical notation - as penrosesche diagrammatic notation , tensor diagram notation or simply Penrose notation called - is one of Roger Penrose proposed notation in physics and mathematics , a (mostly handwritten) visual representation of multi-linear maps or tensors to receive. A diagram consists of closed shapes that are connected by lines.

The notation has been extensively researched by Predrag Cvitanović , who uses this notation to classify classical Lie groups . The notation has been generalized to represent the theory of spin networks in physics and the presence of matrix groups in linear algebra .

Multilinear algebra

In multilinear algebra , every form corresponds to a multilinear function. The lines on shapes represent the inputs or outputs of the function. The connection of these inputs and outputs corresponds to the composition of the respective functions.

Tensors

In tensor algebra , a particular tensor is represented as a particular shape. Lines up and down abstract the upper and lower indices of the respective tensors. Connections between two forms corresponds to the contraction of the indices. One advantage of this notation is that you don't have to invent new letters for new indices. The notation is also expressly independent of the base.

Examples

• 

  vector ${\displaystyle \xi ^{a}}$

• 

  vector ${\displaystyle \eta ^{a}}$

• 

  vector ${\displaystyle \zeta ^{a}}$

• 

  vector ${\displaystyle \beta _{a}}$

• 

  Tensor ${\displaystyle \lambda _{bcd}^{a}}$

• 

  Tensor ${\displaystyle D_{cd}^{ab}}$

• 

  Kronecker Delta ${\displaystyle \delta _{b}^{a}}$

• 

  Hermitian scalar product ( see also: Bra-Ket )
  ${\displaystyle \beta _{a}\,\xi ^{a}}$ ${\displaystyle =\langle \xi |\beta \rangle }$ ${\displaystyle =\xi ^{*}\cdot \beta }$ ${\displaystyle =h(\xi ,\beta )}$
  

• 

  Metric tensor ${\displaystyle g^{ab}}$

• 

  Metric tensor ${\displaystyle g_{ab}}$

• 

  Symmetrization ${\displaystyle Q^{(a_{1}\ldots a_{n})}}$

• 

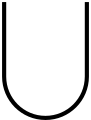
  Asymmetrization ${\displaystyle E_{[a_{1}\ldots a_{n}]}}$

• 

  Tensor ${\displaystyle Q_{fg}^{abc}}$

• 

  ${\displaystyle Q_{fg}^{abc}-2\,Q_{fg}^{bca}}$

• 

  ${\displaystyle Q_{fg}^{abc}-2\,Q_{gf}^{bca}}$

• 

  ${\displaystyle \xi ^{a}\,\lambda _{ab[c}^{(d}\,D_{fg]}^{e)b}}$
  (with  ) ${\displaystyle {}_{{\frac {1}{2!}}\cdot {\frac {1}{3!}}={\frac {1}{12}}}}$

• 

  Levi-Civita symbol ( permutation ) ${\displaystyle \varepsilon _{a_{1}\ldots a_{n}}}$

• 

  ${\displaystyle \epsilon ^{a_{1}\ldots a_{n}}}$

• 

  Faculty ${\displaystyle \varepsilon _{a_{1}\ldots a_{n}}\,\epsilon ^{a_{1}\ldots a_{n}}=n!}$

• 

  Determinant ${\displaystyle \det \mathbf {T} =\det \left(T_{\ b}^{a}\right)}$

• 

  ${\displaystyle \det \left(\mathbf {ST} \right)=}$ ${\displaystyle \det \mathbf {S} \,\det \mathbf {T} }$

• 

  ${\displaystyle \mathbf {T} ^{-1}=\left(T_{\ b}^{a}\right)^{-1}}$
  (Inverse of the matrix ) ${\displaystyle n\times n}$ ${\displaystyle \mathbf {T} }$

• 

  Track function ${\displaystyle \operatorname {Spur} \mathbf {T} =T_{\ a}^{a}}$

• 

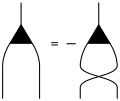
  Structural constant ${\displaystyle \gamma _{\alpha \beta }^{\chi }=-\gamma _{\beta \alpha }^{\chi }}$

• 

  ${\displaystyle \gamma _{[\alpha \beta }^{\xi }\,\gamma _{\chi ]\xi }^{\zeta }=0}$

• 

  ${\displaystyle \gamma _{[\alpha \beta }^{\xi }\,\gamma _{\chi ]\xi }^{\zeta }}$ ${\displaystyle =\gamma _{\alpha \beta }^{\xi }\,\gamma _{\chi \xi }^{\zeta }}$ ${\displaystyle -\gamma _{\alpha \beta }^{\xi }\,\gamma _{\xi \chi }^{\zeta }}$ ${\displaystyle -\gamma _{\xi \beta }^{\zeta }\,\gamma _{\chi \alpha }^{\xi }}$ ${\displaystyle =0}$

• 

  Killing form ${\displaystyle \kappa _{\alpha \beta }}$ ${\displaystyle =\kappa _{\beta \alpha }}$ ${\displaystyle =\gamma _{\alpha \zeta }^{\ \ \xi }\,\gamma _{\beta \xi }^{\ \ \zeta }}$

• 

  Covariant derivative ${\displaystyle 12\nabla _{\mu }\left\{\xi ^{a}\lambda _{ab[c}^{(d}D_{fg]}^{e)b}\right\}}$

• 

  Riemann curvature tensor ${\displaystyle R_{abc}^{\ \ \ d}}$

• 

  Ricci identity ${\displaystyle (\nabla _{a}\,\nabla _{b}-\nabla _{b}\,\nabla _{a})\,\mathbf {\xi } ^{d}}$ ${\displaystyle =R_{abc}^{\ \ \ d}\,\mathbf {\xi } ^{c}}$

• 

  Ricci tensor ${\displaystyle R_{ab}=R_{acb}^{\ \ \ c}}$

• 

  Antisymmetry of the Riemannian curvature tensor ${\displaystyle R_{abc}^{\ \ \ d}=-R_{bac}^{\ \ \ d}}$

• 

  Bianchi symmetry ${\displaystyle R_{[abc]}^{\ \ \ d}}$ ${\displaystyle =R_{abc}^{\ \ \ d}}$ ${\displaystyle +R_{cab}^{\ \ \ d}}$ ${\displaystyle +R_{bca}^{\ \ \ d}}$ ${\displaystyle =0}$

• 

  Bianchi identity ${\displaystyle \nabla _{[a}R_{bc]d}^{\ \ \ e}=0}$

• 

  ${\displaystyle g_{ab}=g_{ba}}$
  (e.g. ) ${\displaystyle \mathbf {g} ^{T}=\mathbf {g} }$

• 

  ${\displaystyle g^{ab}=g^{ba}}$

• 

  ${\displaystyle g_{ab}\,g^{bc}=\delta _{a}^{c}=g^{cb}\,g_{ba}}$

See also

• Abstract index notation

literature

• Roger Penrose : The Road to Reality: A Complete Guide to the Laws of the Universe. Jonathan Cape, London et al. 2004, ISBN 0-224-04447-8 .
• Roger Penrose , Wolfgang Rindler : Spinors and Space-Time: Vol I, Two-Spinor Calculus and Relativistic Fields . Cambridge University Press, 1984, ISBN 0-521-24527-3 .
• Roger Penrose , Wolfgang Rindler : Spinors and Space-Time: Vol. II, Spinor and Twistor Methods in Space-Time Geometry . Cambridge University Press, 1986, ISBN 0-521-25267-9 .

Web links

Commons : Penrose graphical notation  - collection of images, videos and audio files