Price elasticity
The price elasticity measures the relative change in the supply or the demand following a price change .
General
The higher the value of the price elasticity, the more the quantity reacts to the price change. The price elasticity of an overall market tends to be less than the elasticity of an individual good that can be exchanged ( substituted ) for another when the price changes .
Basically, the elasticities can be differentiated between the influence of the demand and the supply volume, which is why four elasticities are named more precisely as a whole. If the price elasticity is mentioned without further specification, the direct price elasticity of demand is usually meant:
A special form of price elasticity is the cross price elasticity , which shows how the price change of one good affects the quantity change of another good:
- Cross-price elasticity of demand
- Cross price elasticity of the supply
In the case of the indirect or cross-price elasticity of demand, a distinction must be made as to whether the products are complementary or competing. If the price of a product is lowered, the demand for a complementary good increases or sales decrease for a competing product or substitute good .
Furthermore, a distinction is made between short-term and long-term elasticity. Since it is z. If, for example, technical progress makes it possible to adapt to certain price changes, the long-term price elasticity is stronger than the short-term price elasticity for many goods, but not for all.
definition
The price elasticity is defined as the relative change in quantity (of the goods offered on the market at this price) divided by the relative change in price . A distinction is made here between different approaches.
Arch elasticity
The arc elasticity with the price and the quantity , where the old price and the new mean, analogously,
- .
One can interpret this elasticity as an approximate average relative change in .
Mean value method
It is a variant of the arch elasticity in which the changes are not related to a fixed value or , but to the mean of and , analogously. You then get
- .
Elasticity function
If a differentiable demand function is available, the question of how the demand changes in the event of a price increase can be answered directly by considering the function. The price elasticity of demand corresponds precisely to the ratio between the relative change in the quantity demanded and the relative change in the price if the price change is allowed to approach zero ( limit value observation ). For the price elasticity of demand we get:
- .
(For details on the derivation, see the article Elasticity (Economy) #An Independent Variable . )
Categorization
The possible elasticities are shown below. Unless otherwise stated, the examples always deal with the effects of a price change on the amount of demand.
Usually a negative sign is observed for the coefficient of elasticity , since a dividend is always negative. For example, a price decrease usually leads to an increase in sales, while a price increase leads to a decrease in sales. Only in the case of abnormal elasticity , such as can occur in luxury goods or hamster purchases, is the elasticity coefficient positive. In this way, conclusions can be drawn about the type of the examined good from the sign .
Quantitatively
To what extent does the price influence the change in quantity in supply and demand?
|
|
||
| presentation | ||
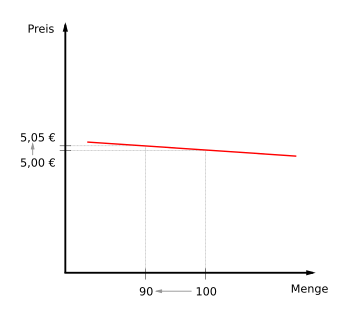
| Explanation | A minimal ( infinitesimal ) change in price causes an infinite change in quantity. The perfect elasticity can only be viewed as a model ; it will not be found in the real economy. | |
| example | A 5 euro banknote at a price of 5.01 euros would not find any buyers. If, on the other hand, the banknote costs exactly 5.00 euros, the requested amount is as large as desired. The consumers actually only buy the banknote when it is needed. At a price of 4.99 euros, it is even infinitely large, since every customer will now try to buy this banknote. | |
|
very elastic |
||
| presentation | ||
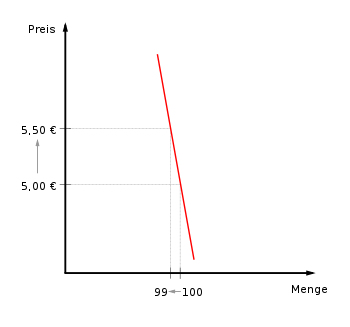
| Explanation | A change in price causes a disproportionate change in quantity. | |
| example | A strong response in demand to price changes can be seen, for example, in the case of good substitutes such as nails of a certain type. If the price is increased, almost all customers may switch to the competition; if the price is reduced, customers switch back again. | |
|
|
||
| presentation | ||
| Explanation | A 1% change in price causes a 1% change in quantity. | |
| example | The case of unit elasticity should not be confused with that of iso-elasticity : in the first case, the elasticity is equal to one at one point of demand. In the second case, the price elasticity of demand is constant; H. the same size for every price. | |
|
|
||
| presentation | ||
| Explanation | A change in price causes a disproportionately low change in quantity. | |
| example | A weak response of demand to price changes is particularly evident in the case of essential economic goods such as food, which are difficult to substitute . Other reasons are the lack of awareness of the price change and the effort involved in searching for substitutes. | |
|
|
||
| presentation | ||
| Explanation | A maximum price change does not change the quantity. | |
| example | There is no reaction of the demand to price changes. This can be seen, for example, in the case of essential medicines, since the same amount is always bought despite price increases. In practice, however, this case finds its limits where all financial resources have been exhausted. So customers are ready to buy the product at any price as long as they can afford it. A classic example of the demand side would be the need for insulin for a diabetic. For the supply side, such a case can arise, for example, when there is simply no more of a good: collector's items (books, LP, stamps) only have a certain number of copies. | |
|
|
||
| presentation | ||
| Explanation | In this special case, the demand is positively elastic; a higher price induces a higher demand.
The price elasticity of the demand for a particular good cannot, however, be positive for every price level; this would require the availability of infinite financial resources from the demanders. |
|
| example | This is the case, for example, if the rising price is associated with an increasing exclusivity of the good ( snob effect , demonstrative consumption ) or if the increase in the price indicates an imminent shortage of the good ( hamster purchase ). The price can also be viewed as a quality indicator, or there is a Giffen good (absolutely inferior good ). | |
|
|
||
| presentation | ||
| Explanation | The demand is called isoelastic if the elasticity at every point is −1. This is the case when a price change changes the quantity demanded to the extent that the product of quantity and price (sales) remains constant. | |
| example | As an example, imagine an equilateral hyperbola whose asymptotes are the axes. | |
Competitive (Triffin's coefficient)
The use of cross price elasticity as an indicator of the strength of competing firms goes back to Robert Triffin . After calculating the cross-price elasticity of demand, in the following Triffin's coefficient e , a distinction is made between three forms of competition:
| There is no competition if the cross price elasticity is zero. The change in the price of supplier A does not affect the sales volume of supplier B. | |
| The smaller e, the lower the competition. If supplier A raises the price for milk by 100% and then the sales volume of milk from manufacturer B only increases by 0.1%, e = 0.001 and thus indicates heterogeneous competition . | |
| The closer e approaches infinity, the greater the competition. A small change in the price of one good already results in a drastic increase in sales of another good; it is homogeneous competition .
e = infinite -> homogeneous competition: If manufacturer A lowers the price of its milk infinitesimally, the sales volume of milk from manufacturer B drops drastically. |
application
When competing for the most precise assessment of customer behavior in marketing , observing the price elasticity of demand helps in the design of a strategic pricing policy . Unlike operational pricing measures, for example, the short-term sales of seasonal goods are used or the leadership of competitive actions, the knowledge of the price elasticity of demand has market of strategic importance. Among other things, it is recorded from which market price an increase in prices lowers the quantity sold so much that the total turnover is lower than before the price increase. In the event that sales of a product or service fall short of expectations, the elasticity can be used to determine whether a price reduction makes sense.
The price elasticity can also be used as a key figure for controlling in the company in order to record the stability of one's own prices in the event of fluctuations in demand.
In the economic framework, price elasticity is used to calculate tax revenue. The higher the elasticity, the more likely the taxed good will no longer be consumed after a tax increase. The tax therefore aims to steer consumer behavior (see also steering tax ). On the other hand, if the elasticity is low, the tax has the character of a revenue tax.
Examples of empirically determined price elasticities of demand
Theoretically, “luxury goods” have a high price elasticity of demand, while “necessary goods” have a low price elasticity of demand. According to Artur Woll, this is initially confusing, since the elasticity of demand along the demand curve can assume all values from zero to infinity. In fact, the elasticities empirically determined for various goods do not spread over this entire range, but mostly within a narrow range. There are therefore “typical” elasticities for certain goods, which, however, vary according to space and time.
For example, the economic historian Hans-Heinrich Bass estimated the price elasticity of the demand for bread grain (rye) in Prussia in the first half of the 19th century with data on meal and slaughter tax at a value of −0.2. According to Gollnick, the price elasticity of demand for bread and baked goods in Germany between 1950 and 1970 was −1.8. Bass' estimate comes closer to the theoretically “expected” value of the price elasticity for this “necessary good” grain. However, the elasticity may simply have shifted over the course of a century
| goods | elasticity | place and time | source |
|---|---|---|---|
| food | −1.3 | Germany 1955–1970 | Woll, Allgemeine Volkswirtschaftslehre, 13th edition. 2000, p. 119 after Gollnick 1975 |
| Fuels | −0.41 | Germany around 1984 | Woll, Allgemeine Volkswirtschaftslehre, 13th edition. 2000, p. 119 after Conrad 1984 |
| Bread grain | −0.23 | Prussia 1838-1850 | Bass, Hungerkrisen in Prussia, 1991, p. 295. |
| dress | −0.16 | Germany 1961–1981 | Woll, Allgemeine Volkswirtschaftslehre, 13th edition. 2000, p. 119 after Hansen 1984 |
| personal hygiene | +0.3 | Germany 1951–1970 | Woll, Allgemeine Volkswirtschaftslehre, 13th edition. 2000, p. 119 after Gollnick 1975 |
Examples
Price drop
A company changes the price of a product from the current 60 to 50 euros. As a result, the sales volume increases from currently 3,000 to 4,000 pieces.
Percentage increase in sales
Percentage price reduction
Price elasticity
The demand is therefore (very) elastic .
Price increase
A retailer increases the price of a branded jacket from currently € 100 to € 105. As a result, demand has dropped from currently 10 to 9 pieces.
Percentage decline in sales
Percentage price increase
Price elasticity
The demand is therefore (very) elastic .
Function describes a change in quantity
There is a relationship between a quantity m and the market price p , which is represented by the following function:
What is the coefficient of elasticity at ?
solution
With this task there are no percentage changes from which the elasticity coefficient could be calculated with the aid of the arch elasticity. The elasticity function mentioned above is therefore used. First the derivation of the price / quantity function has to be created.
Next, the expected quantity is calculated for a price of .
The first derivation of the price / quantity function as well as the price and the calculated quantity can now be used in the elasticity function:
Maximum sales price determination using elasticity
Due to the nature of price elasticity and its course, it can also be used to calculate the sales-maximizing price. To do this, one sets the price elasticity for a certain demand - as usual in the absolute amount - equal to 1.
(As a rule, the demand curve is falling and thus .) If you now solve this formula for p , you get the maximum sales price for the given price-sales function .
See also
literature
- Richard Geml, Hermann Lauer : Marketing and Sales Lexicon . 4th edition. Schäffer-Poeschel, Stuttgart 2008, ISBN 978-3-7910-2798-2 .
- Christian Homburg , Harley Krohmer : Marketing Management. Gabler Verlag, Wiesbaden 2006, ISBN 3-8349-0063-X .
Web links
- Price elasticity - definition in the Gabler Wirtschaftslexikon
- The direct price elasticity mikrooekonomie.de
- Empirical Estimates for Elasticities of Agricultural Goods - Database of the University of Iowa Food and Agricultural Policy Research Institute
Individual evidence
- ^ Gerhard Graf: Fundamentals of Economics. 2nd Edition. Physica-Verlag, 2002, p. 41.
- ↑ Richard Geml / Hermann Lauer, Marketing and Sales Lexicon , 2008, p. 261
- ↑ Example gasoline: In the short term, the price elasticity of the demand for gasoline is relatively inelastic compared to the long term. In the short term, it is not possible to switch to an alternative good. In the long term, more fuel-efficient and smaller cars can be produced. Thus, the long-term price elasticity of the demand for gasoline is relatively more elastic than the short-term. See this discussion ( Memento of the original from August 20, 2010 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. .
- ↑ From Wöhe: Robert Triffin: Monopolistic Competition and General Equilibrium Theory. Cambridge MA 1949, p. 97 ff.
- ^ Artur Woll: General Economics. 13th edition. 2000, p. 119.
- ^ Artur Woll: General Economics. 13th edition. 2000, p. 119.
- ^ Hans-Heinrich Bass: Hunger crises in Prussia in the first half of the 19th century. St. Katharinen 1991, p. 295.
- ^ H. Gollnick: Dynamic Structure of Household Expenditures in the Federal Republic of Germany. Amsterdam 1975.