Role (physics)

A roller (also: pulley ) is a force transducer and machine element consisting of a wheel or a circular disc that is mounted on an axle with as little friction as possible . It is used to guide a rope or a chain. A rolling movement takes place between the roller and the rope or chain . At the edge of the circular disc there is usually a web that prevents the rope from slipping. Rollers are used to change the direction of a tensile force (the force vector ) (without changing the amount of force), to guide the rope or as a compensation element in rope systems. Large pulleys, for example on winding towers or cable cars , are called pulleys . In seafaring, a circular disk with its housing is called a block . Typical applications are rope transmission and devices such as elevators, pulley blocks and cranes .
Fixed and loose roles
A distinction is made between fixed and loose roles:
- A fixed roller is attached so that it does not change position during use. Forces are redirected by means of fixed rollers (for example, pulling a load on a deflected pulling rope). The pulling force remains unchanged, only the pulling direction is influenced. A fixed roller is also called a deflection roller, as it is used to deflect the force.
- Loose rollers lie in the rope guide and are carried by the rope. Each of the two parts of the rope that enclose the loose pulley absorbs 50% of the force. In this way, a load can be lifted with half the effort. The length of the rope to be pulled over the pulley is twice as long as the lifting path , so that and apply.
A combination of loose and fixed rollers forms a pulley .
Example for illustration
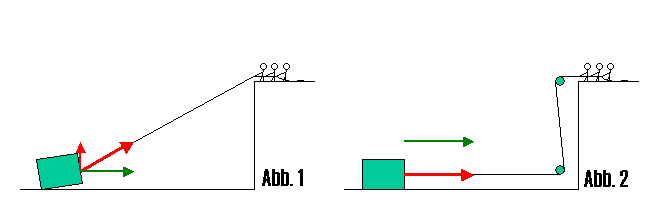
Three people want to pull a box towards the cliff without being able to leave the cliff. A certain amount of force F 3persons can be applied, which is transferred to the crate through the rope with almost no loss. (Shown in the picture by a red vector running with the rope.) Without the pulley (Figure 1), in this case some of the available force is used to lift the box. This is illustrated by the decomposition of the vector F 3Personen into two components. The vertical force component lifts the box, the horizontal one moves the box towards the cliff (green vector). The vertical component becomes larger the closer the box comes to the cliff. Figure 2 shows the application of two fixed roles. The force applied is fully used to move the box (the length of the green corresponds to the length of the red vector).
analysis
- It must be taken into account, however, that the surface friction is unfavorably large with a purely horizontal pull .
- Second, it must be taken into account that the first person near the edge of the rock can bring less horizontal pull into the rope if the rope runs horizontally, but more (purely horizontal pull!) If the rope runs at an angle, because their legs then weigh more than their body weight pressed to the ground before it slips.
- Thirdly, the box is easier to pull (= with less horizontal tensile force component) if the pulling rope runs at an angle, i.e. the box is relieved of its own weight, especially the lower front edge that tends to get caught in the uneven ground.
- Fourth, it is dangerous to deal with a pull rope, especially with several people close to the edge of a cliff. Because the jump from static to sliding friction on the soles of the shoes makes it possible for the person closest to the edge to slip their legs over the edge of the cliff and they would then probably be exposed to the accelerating effect of gravity for some time.
- Fifthly, the - graphically documented - increase in the tensile force - in the direction of the rope - due to the merely slightly Z-shaped guiding of the rope around 2 ideally friction-free functioning pulleys, is remarkable.
- Finally, the special value of the example is based on the rarity in which the pulling of a box to a cliff can be observed in everyday reality.
The mere pulley on a small arm on the scaffolding above, by means of which 1–4 construction buckets with mortar are pulled up by one person below using a handy, handy hemp rope, is just plain banal.
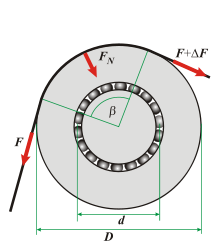
Friction and efficiency
In practice, the following values are assumed for the losses due to the tension in the ropes and the friction of the bearings, whereby the tensile force of the ropes represents:
- Rope tension (depending on construction and load):
- Bearing friction: where and is the coefficient of friction /
For the total losses there are therefore
- .
The efficiency results from it
- .
In practice, the efficiency of a role is as follows:
- for a roller bearing:
- with a plain bearing:
literature
- Douglas C. Giancoli: Physics. Text and exercise book, 3rd edition, Person Education, Munich 2010, ISBN 978-3-86894-023-7 .
- Paul Reis: Textbook of Physics . Quandt and Handel publisher's bookstore, Leipzig 1872.
See also
- Simple machine (the role is one of the simple machines)
- Hinged clamp
- Corrugated gear (a force transmission can be generated by two firmly connected rollers of different diameters)
- Pulley
Web links
- Lexicon of Physics (accessed March 24, 2016)












![{\ displaystyle \ Delta F = \ Delta F_ {1} + \ Delta F_ {2} = 0 {,} 01 \ cdot F + 2 \ mu \ cdot (d / D) \ cdot \ sin (\ beta / 2) \ cdot F = \ left [0 {,} 01 + 2 \ mu \ cdot (d / D) \ cdot \ sin (\ beta / 2) \ right] \ cdot F}](https://wikimedia.org/api/rest_v1/media/math/render/svg/374d93f7011d1adb388e99bec7c153097b340d32)



