Simulated annealing
Simulated Annealing ( simulated cooling / annealing ) is a heuristic approximation method . It is used to find an approximate solution to optimization problems which, due to their high complexity, exclude the complete testing of all possibilities and mathematical optimization methods .
The Metropolis algorithm is the basis for the simulated cooling process . The basic idea is to simulate a cooling process, for example during annealing in metallurgy . After a metal has been heated, the slow cooling ensures that the atoms have sufficient time to arrange themselves and form stable crystals. This achieves a low-energy state close to the optimum. Transferred to the optimization process, the temperature corresponds to a probability with which an intermediate result of the optimization may also deteriorate. In contrast to a local search algorithm, the method can leave a local optimum again. Less favorable interim solutions are accepted because this offers the chance to find a better local optimum.
The algorithm is used, for example, for floor planning in the course of a chip design or for location and route planning.
There are also quantum versions of annealing (with tunneling between the minima) introduced in the 1990s. They were implemented in hardware in adiabatic quantum computers from D-Wave Systems .
motivation
The simulated annealing algorithm is motivated by physical considerations. We are looking for an energetically most favorable state of a system, which can be described with the help of Boltzmann statistics . According to Boltzmann statistics, the probability of encountering a microstate with energy is given by the probability distribution
where is the Boltzmann constant and the temperature. The energy of the energetically most favorable state is . The above proportionality remains when multiplied by an independent factor:
Since it is the energetically most favorable state, applies . Furthermore is and . Thus, the exponent is negative, and its magnitude increases with decreasing temperature, which decreases the probability of finding an excited energy state with at least . If one lowers the temperature of the system slowly, the most energetically favorable state is found with an increasing probability.
Problem
Given is the solution space , a fitness function that assigns a value to each solution , and a termination criterion.
We are looking for an approximate solution of the global minimum of over , i.e. one with the smallest possible value (or also the largest possible, which can simply be reduced to the previous case by negating this).
In addition, an environment concept (see power set ) is required to generate a neighboring solution for a given one .
algorithm
- Initialization:
- choose a starting solution
- put
- choose a sequence of positive temperature values that decreases monotonically towards zero
- Set
- local change:
- randomly pick a neighbor to
- Selection:
- if , put
- otherwise only bet with probability .
- Update best solution so far:
- if , put
- Increment:
- put
- Abort or continue:
- if the termination condition is not met, go to step 2.
Explanations
The greater the deterioration , the smaller the probability that it will be replaced by a worse one . Because it is a monotonically decreasing sequence, the probability also decreases more and more during a program run. The process behaves more and more like a mountaineering algorithm with decreasing amount .
How a neighbor should be chosen depends on the problem at hand. In computer science, is often the value range and is called bit - vector considered. A neighbor of can then e.g. B. can be generated by flipping (inverting) one or a few bits (see Wegener 2005).
Various termination conditions are conceivable. For example, only a maximum number of runs is allowed, sufficient fitness is defined, a lower limit for cooling is defined, or a number of points in time are defined over which no further changes have been made.
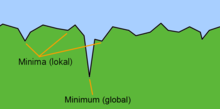
Graphic clarification
The idea of simulated cooling can be illustrated graphically.
Suppose you are looking for the (global) lowest point in a two-dimensional landscape. The landscape itself consists of many dents of different depths. The simple search strategy (search for the next lowest point) corresponds to the behavior of a ball that is exposed in this landscape. It rolls to the nearest local minimum and stays there. During the simulated cooling, the ball is repeatedly given an impact that becomes weaker as the "cooling" increases. This is ideally strong enough to remove the ball from a shallow dent (local minimum), but not enough to escape from the global minimum.

See also
- Acceptance threshold ( threshold accepting )
- Deterministic annealing
- Stochastic tunneling
- Deluge algorithm
- Metropolis algorithm
literature
- Ingo Wegener : Simulated Annealing Beats Metropolis in Combinatorial Optimization . In: Lecture Notes in Computer Science . tape 3580 . Springer, Berlin / Heidelberg 2005, ISBN 978-3-540-27580-0 , pp. 589–601 , doi : 10.1007 / 11523468 (For a problem that is easy to describe, it is shown that, regardless of the temperature, the simulated cooling is more efficient than the Metropolis algorithm .).
Web links
- Interactive JavaScript for demonstration ( Memento from March 13, 2015 in the Internet Archive )
- Interactive demonstration to try out
- C # implementation and application to minimize and address the traveling salesman problem
- Simulated Annealing in C ++ optimization library cppOpt cppOpt or OptSimulatedAnnealing.h
Individual evidence
- ↑ Bogatzki, A .: Factory planning: Procedure for optimizing machine installation. Dissertation University of Wuppertal (1998). Roderer 1998. ISBN 978-3-89073-234-3
- ↑ T. Kadowaki, H. Nishimori, Quantum annealing in the transverse Ising model , Phys. Rev. E, Volume 58, 1998, p. 5355
- ↑ AB Finilla, MA Gomez, C. Sebenik, JD Doll, Quantum annealing: A new method for minimizing multidimensional functions , Chem. Phys. Lett., Vol. 219, 1994, p. 343
- ↑ JP Dr. A. Arnold, University of Stuttgart, Institute for Computer Physics , script for the lecture Physics on the Computer (PDF; 3.5 MB) p. 181 ff.
- ↑ Google TechTalk Lecture A short but very understandable explanation of the topic can be found from minute 35.