Soma cube
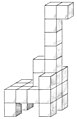
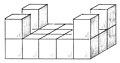
The soma cube is a mechanical game of patience in which a cube is to be assembled from seven individual parts. Each individual part is a poly cube , i.e. That is, it is itself composed of smaller, identical cubes, and all seven parts are different (as in pentominos ).
The game serves to train spatial imagination as well as problem-solving .
Possible tasks
Build a cube
The one tri-cube (triplet) and the six tetra-cubes (four-of-a-kind) in the game contain the smaller, identical cubes. John Horton Conway and Mike JT Guy found out in 1961 that there are exactly 240 different possible solutions for the basic task of the game of assembling the seven poly cubes to form a 3x3x3 cube, apart from rotations and reflections of the cube. As Brunvoll et al. more precisely, the soma cube can be put together in exactly 480 ways that cannot be converted into one another by rotating the soma cube; these 480 solutions are composed of 240 pairs of solutions which are mirror symmetrical to one another (i.e., plane symmetrical).
There are only a few ways to assemble the poly cube into a 3x3x3 cube in such a way that it does not fall apart if you only support the cube in the middle of the underside (“balanced Soma cube”).
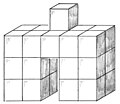
Soma tangram
In Soma Tangram , a body, given by an oblique image , has to be composed of Soma parts.
diamond
giraffe
upturned table
goal
history
The Soma cube was invented in 1936 by Piet Hein during a lecture on quantum mechanics by Werner Heisenberg . The name is the fictional, the establishment consumed pastime drug soma from Aldous Huxley's dystopischem novel Brave New World (German Brave New World ) be ajar. Martin Gardner made the cube famous when he discussed it in his Mathematical Games column in Scientific American magazine in 1958 . Ever since the Swiss teachers and trainers Ueli Hirt and Sandra Meister worked out teaching material for the Soma cube and presented it at a conference of the Society for Didactics of Mathematics in Ludwigsburg in 2001 , it has been used in particular in mathematics lessons in primary schools.
The main inner belt asteroid (2815) Soma is named after the Soma cube.
To the seven individual parts
The seven individual parts are all possible irregular bodies (poly cubes) that can be put together from three or four cubes. Irregular here means that there is at least one re-entrant edge (or, in other words, that the poly cube is not convex). This means that there is exactly one threesome (“v”) and six foursome. The foursome has three flat and three 3D shapes. The flat ones are L-, S-, and T-shaped.
Variation Babylonia
The Babylonia variation of the Soma dice game includes two three-part and seven four-part building blocks. The two three-part building blocks are black and white, the four-part building blocks are in the colors blue, yellow, green, orange, red and purple as well as natural. A D6 die only shows the colors black and white, a colored D6 die shows all the aforementioned colors except nature. Now you have to use the dice to determine the colors of two building blocks that should not be used in the construction of the Soma cube. The natural-colored building block must always be used.
Pieces and dice of the game Babylonia
Color cubes of the game Babylonia
literature
- Elwyn R. Berlekamp; John H. Conway; Richard K. Guy: Winning. Strategies for Math Games. Vol. 4: Solitaire games. Braunschweig; Wiesbaden: Vieweg, 1985, pp. 41-42 (Soma), 43-45 (The hidden secrets of Soma), 107-110 (The Somap).
- Martin Gardner: The Second Scientific American Book of Mathematical Puzzles and Diversions. New York: Simon and Schuster, 1961. ND Chicago: University of Chicago Press, 1987, chap. 6, pp. 65-77 (The Soma Cube).
Web links
Individual evidence
- ^ Elwyn R. Berlekamp, John H. Conway, Richard K. Guy: Winning Ways for Your Mathematical Plays, Vol. 2 . Academic Press, London, 1982
- ^ Soma Cube , Wolfram MathWorld
- ↑ Jon Brunvoll, Bjørg Cyvin, Einar Cyvin, Sven Cyvin, Aage Paus, Martin Stølevik, Reidar Stølevik: The computerized Soma cube . Computers & Mathematics with Applications, Vol. 12, 1986, pp. 113-121
- ↑ The 4th solution to a balanced Soma cube
- ↑ Soma figures overview (pentoma.de)
- ↑ Denmark: The Soma Cube ( Memento of the original from December 23, 2016 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. . SAMMS - Student Academy of Mathematics in Münster
- ↑ Martin Gardner: Mathematical puzzles and diversions Vol. 1/2. Simon and Schuster, New York, 1959/1961 (German as mathematical puzzles and problems , Vieweg Verlag, 1964)
- ↑ See Birgit Kaltenmorgen: The mathematical patchworker. Puzzle and handicraft fun for puzzle fans . Wagner, Gelnhausen 2008, p. 113 ( limited preview in the Google book search).
- ^ Martin Gardner: A game in which standard pieces composed of cubes are assembled into larger forms. Scientific American, September 1958
- ↑ Ueli Hirt, Sandra Luginbühl: Games with the Somawürfel , Kallmeyer, 2003
- ^ Dorothea Winkler: Card files for the Soma cube. Westermann Schulbuch Verlag, 2006
- ^ Lutz D. Schmadel : Dictionary of Minor Planet Names . Fifth Revised and Enlarged Edition. Ed .: Lutz D. Schmadel. 5th edition. Springer Verlag , Berlin , Heidelberg 2003, ISBN 978-3-540-29925-7 , pp. 186 (English, 992 pp., Link.springer.com [ONLINE; accessed September 15, 2019] Original title: Dictionary of Minor Planet Names . First edition: Springer Verlag, Berlin, Heidelberg 1992): “1982 RL. Discovered 1982 Sept. 15 by E. Bowell at Anderson Mesa. "
