Steiner's theorem

Illustration of Steiner's theorem:
axis of rotation 1 goes through the center of gravity of the body of the mass . Axis of rotation 2 is shifted by the distance d. ${\displaystyle m}$

The Steiner's theorem (also Steiner's theorem , Steiner rule , set of Huygens-Steiner or parallel axis theorem ) is used to calculate the moment of inertia of a rigid body for parallel displaced axes of rotation . The sentence goes back to studies by Jakob Steiner and Christiaan Huygens .

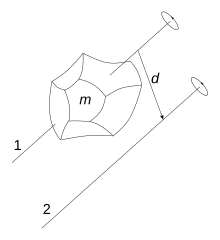
The moment of inertia is not a fixed property of a body, but also depends on the axis of rotation. If the moment of inertia of an axis of rotation through the center of mass is known, Steiner's theorem can be used to calculate the moment of inertia for all axes of rotation that are parallel to it.

The theorem is also used to determine geometrical moments of inertia of cross-sections of beams .

Application to moments of inertia

Moments of inertia are usually tabulated for axes of rotation through the center of mass. If the moment of inertia is required for a parallel axis of rotation , Steiner's theorem can be applied and the moment of inertia results in: ${\displaystyle 1}$ ${\displaystyle 2}$ ${\displaystyle J_{2}}$

${\displaystyle J_{2}=J_{\text{1}}^{(S)}+m\,d^{2}}$

It is the moment of inertia of the body mass of the axis of rotation , the (practically equal to the center of mass by its center of gravity passes) and parallel at a distance from the axis of rotation lies. ${\displaystyle J_{\text{1}}^{(S)}}$ ${\displaystyle m}$ ${\displaystyle 1}$ ${\displaystyle d}$ ${\displaystyle 2}$

When applying Steiner's theorem, two things must be observed:

• A body's moment of inertia is lowest when the axis of rotation passes through the center of gravity. This follows from the fact that the Steiner part is always positive if one carries out a shift away from the center of gravity.
• By applying Steiner's theorem several times, the moment of inertia can be calculated for any parallel axis, even if the initially given moment of inertia does not go through the center of mass.

Application to geometrical moments of inertia

If the centroid of a body cross-section is not in the origin of the coordinate system, its area moment of inertia can be calculated using Steiner's theorem:

${\displaystyle J_{{\bar {y}}{\bar {y}}}=J_{yy}+{\bar {z}}_{S}^{2}\cdot A}$

${\displaystyle J_{{\bar {z}}{\bar {z}}}=J_{zz}+{\bar {y}}_{S}^{2}\cdot A}$

${\displaystyle J_{{\bar {y}}{\bar {z}}}=J_{yz}+{\bar {y}}_{S}\cdot {\bar {z}}_{S}\cdot A}$

For , the distance between the center of the area and the origin is squared, multiplied by the area of ​​the cross section and added to the area moment of inertia (recorded in the table). It can be seen that the Steiner term is omitted. ${\displaystyle J_{y}}$ ${\displaystyle {\bar {z}}_{S}}$ ${\displaystyle A}$ ${\displaystyle z=0}$

It is practical that you can use these formulas to divide complex (e.g. T-beams ) into simple bodies (e.g. rectangles) whose area moment of inertia is already known.

For example then applies: ${\displaystyle J_{y}}$

${\displaystyle {\begin{aligned}J_{y}&=\int _{A}z^{2}\cdot {\mathit {d}}A\\&=\int _{A_{1}}z^{2}\cdot {\mathit {d}}A+\int _{A_{2}}z^{2}\cdot {\mathit {d}}A+\dots +\int _{A_{n}}z^{2}\cdot {\mathit {d}}A\\&=J_{{\bar {y}}1}+J_{{\bar {y}}2}+\dots +J_{{\bar {y}}n}\end{aligned}}}$,

where is the area of ​​the figure and until are the partial areas created by the decomposition. ${\displaystyle A}$ ${\displaystyle A_{1}}$ ${\displaystyle A_{n}}$

Generalization to inertia tensors

If a body has a mass and, in relation to the center of gravity, the inertia tensor , then the inertia tensor results in a coordinate system shifted parallel around the vector by the sum of and the inertia tensor of a mass point of the mass and the position vector : ${\displaystyle m}$ ${\displaystyle I^{(S)}}$ ${\displaystyle I}$ ${\displaystyle {\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}}$ ${\displaystyle I^{(S)}}$ ${\displaystyle m}$ ${\displaystyle {\vec {a}}}$

${\displaystyle I_{ij}=I_{ij}^{(S)}+m\left(\sum _{k}a_{k}^{2}\,\delta _{ij}-a_{i}\,a_{j}\right)}$

d. H.

${\displaystyle {\begin{aligned}I&=I^{(S)}+m{\begin{pmatrix}a_{2}^{2}+a_{3}^{2}&-a_{1}a_{2}&-a_{1}a_{3}\\-a_{1}a_{2}&a_{1}^{2}+a_{3}^{2}&-a_{2}a_{3}\\-a_{1}a_{3}&-a_{2}a_{3}&a_{1}^{2}+a_{2}^{2}\end{pmatrix}}\\&=I^{(S)}+m\,{\tilde {a}}^{T}\,{\tilde {a}}\end{aligned}}}$

in which

${\displaystyle {\tilde {a}}={\begin{pmatrix}0&-a_{3}&a_{2}\\a_{3}&0&-a_{1}\\-a_{2}&a_{1}&0\end{pmatrix}}}$

or in sum convention with the totally antisymmetric ε-tensor

${\displaystyle {\tilde {a}}_{ij}=-\epsilon _{ijk}\,a_{k}}$

Therefore also applies

${\displaystyle -{\tilde {a}}={\tilde {a}}^{T}}$

As a result of the shift, it can happen that the axes of the new coordinate system no longer coincide with the main axes of inertia due to the new point.

Derivation

Sketch for derivation

If one looks at a rigid body in a coordinate system, the origin of which coincides with its center of mass and places the axis of rotation parallel to the z-direction, the moment of inertia of this axis is defined as ${\displaystyle B}$

${\displaystyle J_{B}=\sum _{i}m_{i}\left[(x_{i}-x_{B})^{2}+(y_{i}-y_{B})^{2}\right]}$

Whereby the sum runs over all mass points of the body, the location of the respective mass point is marked with and the axis of rotation lies on the straight line parallel to the z-axis through the point . ${\displaystyle m_{i}}$ ${\displaystyle (x_{i},y_{i},z_{i})}$ ${\displaystyle (x_{B},y_{B})}$

Expanding the brackets lists

${\displaystyle J_{B}=\underbrace {\sum _{i}m_{i}(x_{i}^{2}+y_{i}^{2})} _{J_{A}^{(S)}}-2x_{B}\underbrace {\sum _{i}m_{i}x_{i}} _{=0}-2y_{B}\underbrace {\sum _{i}m_{i}y_{i}} _{=0}+\underbrace {(x_{B}^{2}+y_{B}^{2})} _{=d^{2}}\underbrace {\sum _{i}m_{i}} _{=m}}$

The first term corresponds to the moment of inertia of the axis of rotation through the center of mass (and parallel to the z-axis). The second and third terms are zero, since they correspond to the definition of the center of mass and this is precisely at the origin. According to Pythagoras , the fourth term specifies the square of the distance between the axis of rotation and the origin multiplied by the total mass of the body under consideration. If you write the distance as , Steiner's theorem results as ${\displaystyle B}$ ${\displaystyle m=\sum _{i}m_{i}}$ ${\displaystyle d^{2}=x_{B}^{2}+y_{B}^{2}}$

${\displaystyle J_{B}=J_{A}^{(S)}+md^{2}}$

literature

• Alfred Böge: Technical mechanics: statics - dynamics - fluid mechanics - strength theory . Springer DE, ISBN 978-3-8348-8107-6 ( limited preview in the Google book search).
• Wolfgang Demtröder : Experimental Physics 1: Mechanics and Warmth . Springer DE, 2008, ISBN 978-3-540-79295-6 , pp. 146 ( limited preview in Google Book search).
• Christian Spura: Technische Mechanik 2. Elstostatik , Springer Vieweg, Wiesbaden 2019, ISBN 978-3-658-19978-4
• Karl-Eugen Kurrer : History of Structural Analysis. In Search of Balance , Ernst and Son, Berlin 2016, p. 89, ISBN 978-3-433-03134-6

Individual evidence

1. ↑ Hans J. Paus: Physics in experiments and examples . Hanser Verlag, 2007, ISBN 978-3-446-41142-5 , pp. 83 ( limited preview in Google Book search).
2. ↑ Douglas C. Giancoli: Physics: Teaching and practice book . Pearson Germany, 2010, p. 342 ( limited preview in Google Book search).