
The faculty and the Stirling formula
The Stirling formula is a mathematical formula that can be used to calculate approximate values for large faculties . It is named after the Scottish mathematician James Stirling .
Basics
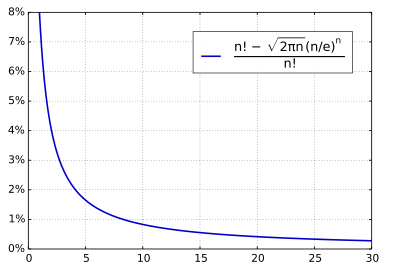
Relative deviation of the simple Stirling formula from the faculty as a function of n
The Stirling formula in its simplest form is an asymptotic formula

For the individual elements of this formula see factorial (!), Square root (√), circle number (π) and Euler's number (e).
A derivation can be found in the article Saddle Point Approximation .
More precisely applies to :


In particular, the limit of the fraction for equals 1.

The Stirling series for according to the Euler-MacLaurin empirical formula is


where the -th denotes Bernoulli number . As an approximation, one only considers a finite number of terms. The error is in the order of magnitude of the first neglected link. Example: if you break off after the third term, the absolute error is less than . The series itself does not converge for solid , it is an asymptotic series .




For satisfies a member for a relative error less than one percent:


For satisfy two members for a relative error less than 0.1 per cent:


For small , a simple formula for can be derived from the formula for four terms . With



the approximation results

The error is (with minimal additional computing effort to calculate the first two terms) smaller than 3% for , smaller than 1% for and smaller than 0.1% for .



Inserting it into the exponential function results in the asymptotic expansion :


and by inserting the Stirling series into the series of the exponential function:

whereby the coefficients do not satisfy any simple law of formation.

Derivation of the first two terms
The formula is often used in statistical physics for the limiting case of large numbers of particles, as they occur in thermodynamic systems ( particle size range). For thermodynamic considerations it is mostly sufficient to consider the first two terms . This formula can be easily obtained by using only the first term of the Euler-MacLaurin formula :


![\ ln (N!) = \ sum _ {n = 1} ^ {N} \ ln (n) \ approx \ int _ {1} ^ {N} \ ln (x) \, \ mathrm {d} x = \ left [x \ ln (x) -x \ right] _ {1} ^ {N} = N \ ln (N) -N + 1 \ approx N \ ln (N) -N](https://wikimedia.org/api/rest_v1/media/math/render/svg/1064b5b9750cb6416c2eb6fcd4594e683724f3eb)
and is then used in this form:
-

Generalization: Stirling formula for the gamma function
For all true

-
 ,
,
where is a function that fulfills for all .



For the individual elements of this formula see gamma function ( ), square root (√), circle number (π) and Euler's number (e).

The value of an approximation of according to the above formula with is always a bit too small for all . The relative error is, however, for less than 1% and for less than 0.1%.





It applies to everyone 
-
 ,
,
which results in the approximation formulas of the previous section as a special case.
Applications
The Stirling formula is used wherever the exact values of a faculty are not important. Particularly when calculating the information of a message and when calculating the entropy of a statistical ensemble of subsystems, the Stirling formula results in great simplifications.
Example: Given a system with different subsystems, each of which can assume different states. It is also known that the state can be assumed with the probability . Subsystems must be in the state and it applies . The number of possible distributions of a system described in this way is then








and for its entropy applies


By means of the Stirling formula one can now simplify this formula
except for errors in the order 

|

|
|
|

|
|
|

|
|
|

|
|
|

|
This results in the well-known formula for the entropy of each of the subsystems


The formula for the information content of an equally defined system is obtained in a similar way (except for a constant prefactor)

See also
literature
Web links
Remarks
-
↑ This is equated with 1, i.e. the limit value for at position 0.


-
↑ In the OEIS there are series for numerators and denominators of , together with comments and references, on Mathworld also formulas for the education law (all in English!) .

-
↑ G. Joos: Textbook of theoretical physics , 1956, p. 516


























![\ ln (N!) = \ sum _ {n = 1} ^ {N} \ ln (n) \ approx \ int _ {1} ^ {N} \ ln (x) \, \ mathrm {d} x = \ left [x \ ln (x) -x \ right] _ {1} ^ {N} = N \ ln (N) -N + 1 \ approx N \ ln (N) -N](https://wikimedia.org/api/rest_v1/media/math/render/svg/1064b5b9750cb6416c2eb6fcd4594e683724f3eb)































