Stirling formula

The faculty and the Stirling formula

The Stirling formula is a mathematical formula that can be used to calculate approximate values for large faculties . It is named after the Scottish mathematician James Stirling .

Basics

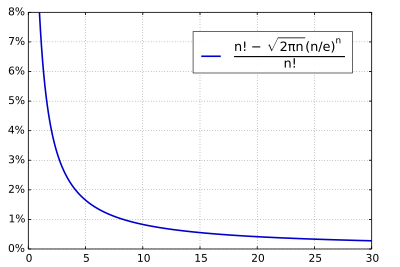
Relative deviation of the simple Stirling formula from the faculty as a function of n

The Stirling formula in its simplest form is an asymptotic formula

${\displaystyle n!\sim {\sqrt {2\pi n}}\;\left({\frac {n}{\mathrm {e} }}\right)^{n},\qquad n\to \infty .}$

For the individual elements of this formula see factorial (!), Square root (√), circle number (π) and Euler's number (e).

A derivation can be found in the article Saddle Point Approximation .

More precisely applies to : ${\displaystyle n>0}$

${\displaystyle 1<\mathrm {e} ^{1/(12n+1)}<{\frac {n!}{{\sqrt {2\pi n}}\cdot ({\frac {n}{\mathrm {e} }})^{n}}}<\mathrm {e} ^{1/(12n)}<1+{\frac {1}{11n}}}$

In particular, the limit of the fraction for equals 1. ${\displaystyle n\to \infty }$

The Stirling series for according to the Euler-MacLaurin empirical formula is ${\displaystyle \ln(n!)=\sum _{i=1}^{n}\ln(i)}$

${\displaystyle \ln(n!)\simeq n\ln(n)-n+{\tfrac {1}{2}}\ln(2\pi n)+{\frac {1}{12n}}-{\frac {1}{360n^{3}}}+\cdots +{\frac {B_{2k}}{(2k-1)2k}}\cdot {\frac {1}{n^{2k-1}}}+\cdots ,\quad n\to \infty }$

where the -th denotes Bernoulli number . As an approximation, one only considers a finite number of terms. The error is in the order of magnitude of the first neglected link. Example: if you break off after the third term, the absolute error is less than . The series itself does not converge for solid , it is an asymptotic series . ${\displaystyle B_{k}}$ ${\displaystyle k}$ ${\displaystyle 1/(12n)}$ ${\displaystyle n}$

For satisfies a member for a relative error less than one percent: ${\displaystyle n>7{,}31\cdot 10^{43}}$

${\displaystyle \ln(n!)\approx n\cdot \ln(n)}$

For satisfy two members for a relative error less than 0.1 per cent: ${\displaystyle n>751}$

${\displaystyle \ln(n!)\approx n\cdot \ln(n)-n}$

For small , a simple formula for can be derived from the formula for four terms . With ${\displaystyle n}$ ${\displaystyle n!}$

${\displaystyle {\mathrm {e} }^{1/(12n)}\approx 1+{\frac {1}{12n}}\approx {\sqrt {1+{\frac {1}{6n}}}}}$

the approximation results

${\displaystyle n!\approx {\sqrt {2\pi n}}\;\left({\frac {n}{\mathrm {e} }}\right)^{n}\;{\mathrm {e} }^{1/(12n)}\approx {\sqrt {2\pi n}}\;\left({\frac {n}{\mathrm {e} }}\right)^{n}{\sqrt {1+{\frac {1}{6n}}}}={\sqrt {{\pi \over 3}(6n+1)}}\;\left({\frac {n}{\mathrm {e} }}\right)^{n}}$

The error is (with minimal additional computing effort to calculate the first two terms) smaller than 3% for , smaller than 1% for and smaller than 0.1% for . ${\displaystyle n=0}$ ${\displaystyle n>0}$ ${\displaystyle n>2}$

Inserting it into the exponential function results in the asymptotic expansion : ${\displaystyle n!}$

${\displaystyle n!\simeq n^{n}\cdot {\sqrt {2\pi n}}\cdot \mathrm {e} ^{-n+{\frac {1}{12n}}-{\frac {1}{360n^{3}}}+\cdots +{\frac {B_{2k}}{(2k-1)2k}}\cdot {\frac {1}{n^{2k-1}}}+\cdots },\quad n\to \infty }$

and by inserting the Stirling series into the series of the exponential function:

${\displaystyle n!\simeq n^{n}\cdot {\sqrt {2\pi n}}\,\cdot \,\mathrm {e} ^{-n}\,\cdot \,\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots +{\frac {C_{k}}{n^{k}}}+\cdots \right),\quad n\to \infty }$

whereby the coefficients do not satisfy any simple law of formation. ${\displaystyle C_{k}}$

Derivation of the first two terms

The formula is often used in statistical physics for the limiting case of large numbers of particles, as they occur in thermodynamic systems ( particle size range). For thermodynamic considerations it is mostly sufficient to consider the first two terms . This formula can be easily obtained by using only the first term of the Euler-MacLaurin formula : ${\displaystyle 10^{23}}$ ${\displaystyle \ln(N!)\approx N\ln(N)-N}$

${\displaystyle \ln(N!)=\sum _{n=1}^{N}\ln(n)\approx \int _{1}^{N}\ln(x)\,\mathrm {d} x=\left[x\ln(x)-x\right]_{1}^{N}=N\ln(N)-N+1\approx N\ln(N)-N}$

and is then used in this form:

${\displaystyle N!\approx \left({\frac {N}{\mathrm {e} }}\right)^{N}.}$

Generalization: Stirling formula for the gamma function

For all true ${\displaystyle x>0}$

${\displaystyle \Gamma (x)={\sqrt {2\pi /x}}\,\left({\frac {x}{\mathrm {e} }}\right)^{x}\,\mathrm {e} ^{\mu (x)}}$,

where is a function that fulfills for all . ${\displaystyle \mu }$ ${\displaystyle 0<\mu (x)<1/(12x)}$ ${\displaystyle x>0}$

For the individual elements of this formula see gamma function ( ), square root (√), circle number (π) and Euler's number (e). ${\displaystyle \Gamma }$

The value of an approximation of according to the above formula with is always a bit too small for all . The relative error is, however, for less than 1% and for less than 0.1%. ${\displaystyle x>0}$ ${\displaystyle \Gamma (x)}$ ${\displaystyle \mu =0}$ ${\displaystyle x\geq 9}$ ${\displaystyle x\geq 84}$

It applies to everyone ${\displaystyle n\in \mathbb {N} }$

${\displaystyle n!=n\Gamma (n)=n{\sqrt {2\pi /n}}\,\left({\frac {n}{\mathrm {e} }}\right)^{n}\,\mathrm {e} ^{\mu (n)}={\sqrt {2\pi n}}\,\left({\frac {n}{\mathrm {e} }}\right)^{n}\,\mathrm {e} ^{\mu (n)}}$,

which results in the approximation formulas of the previous section as a special case.

Applications

The Stirling formula is used wherever the exact values ​​of a faculty are not important. Particularly when calculating the information of a message and when calculating the entropy of a statistical ensemble of subsystems, the Stirling formula results in great simplifications.

Example: Given a system with different subsystems, each of which can assume different states. It is also known that the state can be assumed with the probability . Subsystems must be in the state and it applies . The number of possible distributions of a system described in this way is then ${\displaystyle N}$ ${\displaystyle m}$ ${\displaystyle i}$ ${\displaystyle \omega _{i}}$ ${\displaystyle N_{i}}$ ${\displaystyle i}$ ${\displaystyle N_{i}/N=\omega _{i}}$

${\displaystyle N!/(N_{1}!\,N_{2}!\,\ldots \,N_{m}!)}$

and for its entropy applies ${\displaystyle \sigma }$

${\displaystyle \sigma =\ln(N!)-\ln(N_{1}!)-\ldots -\ln(N_{m}!).}$

By means of the Stirling formula one can now simplify this formula except for errors in the order ${\displaystyle O(\ln(N))}$

${\displaystyle \sigma \,}$	${\displaystyle =N(\ln N-1)-N_{1}(\ln N_{1}-1)-\ldots -N_{m}(\ln N_{m}-1)}$
	${\displaystyle =N\ln N-N_{1}\ln N_{1}-\ldots -N_{m}\ln N_{m}}$
	${\displaystyle =(N_{1}+\ldots +N_{m})\ln N-N_{1}\ln N_{1}-\ldots -N_{m}\ln N_{m}}$
	${\displaystyle =-N_{1}\ln(N_{1}/N)-\ldots -N_{m}\ln(N_{m}/N)}$
	${\displaystyle =-N\sum _{i=1}^{m}(\omega _{i}\ln \omega _{i})}$

This results in the well-known formula for the entropy of each of the subsystems ${\displaystyle N}$

${\displaystyle \sigma =-\sum _{i=1}^{m}\omega _{i}\ln(\omega _{i})}$

The formula for the information content of an equally defined system is obtained in a similar way (except for a constant prefactor)

${\displaystyle I=-\sum _{i=1}^{m}\omega _{i}\log _{2}{(\omega _{i})}}$

See also

• Gamma function
• Burnside formula

literature

• Eberhard Freitag, Rolf Busam: Function theory . 2nd Edition. Springer-Verlag, Berlin 1995.
• Konrad Königsberger : Analysis 1 . Springer, Heidelberg 2003, ISBN 3-540-40371-X .

Web links

• Eric W. Weisstein : Stirling's Approximation . In: MathWorld (English).
• Pedro Sanchez, Aaron Krowne, Raymond Puzio and others a .: Stirling's approximation . In: PlanetMath . (English)
• Peter Luschny: Approximation Formulas for the Factorial Function . Variants and alternatives to the Stirling formula (English).

Remarks

1. ↑ This is equated with 1, i.e. the limit value for at position 0. ${\displaystyle 0^{0}}$ ${\displaystyle x^{x}}$
2. ↑ In the OEIS there are series for numerators and denominators of , together with comments and references, on Mathworld also formulas for the education law (all in English!) . ${\displaystyle C_{k}}$
3. ↑ G. Joos: Textbook of theoretical physics , 1956, p. 516