Stop time

Hitting time as an example of a stopping time

In stochastics , the term stop time refers to a special type of random variable that is defined on filtered probability spaces. Stop times are not only important for the theory of stochastic processes (for example, in the localization of process classes or investigations into stopped processes ), but also of practical relevance, for example for the problem of the optimal exercise time for American options .

In the specialist literature translated from Russian into English, there are also the terms Markov moment (German Markov moment ) or Markov time (German Markov time ).

definition

A probability space is given . ${\displaystyle (\Omega ,{\mathcal {A}},P)}$

Discreet case

If there is a filtration in , it is called a random variable ${\displaystyle \mathbb {F} =({\mathcal {F}}_{n})_{n\in \mathbb {N} _{0}}}$ ${\displaystyle {\mathcal {A}}}$

${\displaystyle \tau \colon \Omega \to \mathbb {N} _{0}\cup \{\infty \}}$

a stop time (regarding ) when ${\displaystyle \mathbb {F} }$

${\displaystyle \{\tau =n\}=\{\omega \in \Omega :\tau (\omega )=n\}\in {\mathcal {F}}_{n}{\text{ für alle }}n\in \mathbb {N} _{0}}$

is.

General case

Given an ordered index set that is an interval off . If there is a filtration in , it is called a random variable ${\displaystyle T}$ ${\displaystyle [0,\infty ]}$ ${\displaystyle \mathbb {F} =({\mathcal {F}}_{t})_{t\in T}}$ ${\displaystyle {\mathcal {A}}}$

${\displaystyle \tau \colon \Omega \to T}$

a stop time (regarding ) when ${\displaystyle \mathbb {F} }$

${\displaystyle \{\tau \leq t\}=\{\omega \in \Omega :\tau (\omega )\leq t\}\in {\mathcal {F}}_{t}{\text{ für alle }}t\in T}$.

Finite stop time

A stop time is called a finite stop time if ${\displaystyle \tau }$

${\displaystyle P(\tau <\infty )=1}$

is.

comment

It should be noted that the property of being a stop time is not a property of the random variable alone, but a property of the random variable in connection with a filtration. Therefore, when specifying or defining, the filtration must always be given.

interpretation

A stopping time can be interpreted as the waiting time that elapses before a certain random event occurs. If, as usual, the filtering gives the information available at different times, the above condition means that it should be known at all times whether this event has already occurred or not.

Examples

• A gambler starts playing with a starting capital of € 10 at the time; every minute he plays a game (which, for the sake of simplicity, does not take any time) in which he has a 50 percent chance of winning one euro and otherwise losing one euro (the player's account balance is then a martingale ). The waiting time until the player has gambled away all of his money is an example of a stopping time with regard to the natural filtration of the experiment: at any point in time the player knows whether he is already broke or not. In contrast, the waiting time until the moment of your penultimate game would not be a stop time: the moment you play your penultimate game, you don't yet know that the next game will be the last. ${\displaystyle t=0}$

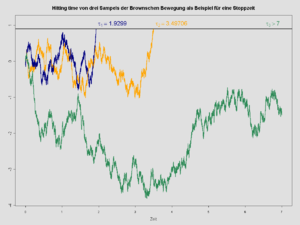
• The hitting time of a Wiener process with drift to the level is defined as . ${\displaystyle (W_{t})_{t\geq 0}}$ ${\displaystyle \mu }$ ${\displaystyle a>0}$ ${\displaystyle \tau _{a}(\omega )=\inf\{t\geq 0:W_{t}(\omega )=a\}}$

${\displaystyle \tau _{a}}$is a stop time. It is after inverse Gaussian distribution distributed, the density is

${\displaystyle f_{IG}(t)={\frac {a\exp(a\mu )}{\sqrt {2\pi }}}t^{-3/2}\exp \left(-{\frac {1}{2}}(a^{2}t^{-1}+\mu ^{2}t)\right),\quad t>0}$.

Example of a hitting time: The two-dimensional Brownian movement touches the ellipse at some point.

• If, more generally, a real-valued, adapted Càdlàg process , i.e. a stochastic process , whose paths are all continuous on the right-hand side and have limit values ​​from the left, and is a closed set , then the meeting time of in is defined as ${\displaystyle (X_{t})_{t\geq 0}}$ ${\displaystyle A\subseteq \mathbb {R} }$ ${\displaystyle X}$ ${\displaystyle A}$

${\displaystyle \tau _{A}(\omega ):=\inf\{t\geq 0:\;X_{t}(\omega )\in A\}}$

a stop time. thus indicates the infimal point in time at which the crowd first entered. It is essential that it is completed: At the time, it could already be on the edge of , but not yet in , and enter the crowd immediately afterwards. Then it would be (note the infimum), but it is not yet known whether or not to enter immediately. ${\displaystyle \tau _{A}}$ ${\displaystyle X}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle t}$ ${\displaystyle X}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \tau _{A}=t}$ ${\displaystyle t}$ ${\displaystyle A}$

Derived Concepts

Stopped process

→ Main article : Stopped process

A stopped process is a combination of a stochastic process and a stop time that takes on values ​​in the index set ("time set") of the stochastic process. Stopped processes are processes that are stopped after a random time or that no longer change their value. For example, you model exit strategies for a time sequence of games of chance.

Localization

→ Main article : Localization (stochastics)

Localization is understood to be the extension of a process class that has a certain property to include the set of all processes that have been stopped with increasing sequences of stopping times also have this property. Typical examples are the martingales and the local martingales .

σ-algebra of the τ past

→ Main article : σ-algebra of the τ-past

The σ-algebra of the τ-past is a special σ-algebra , which is defined by the filtration and the stopping time. It is used, for example, in the definition of the strong Markov property and the Optional Sampling Theorem .

Calculation rules

Let there be and stop times regarding a filtration as well ${\displaystyle \sigma ,\tau }$ ${\displaystyle \tau _{j}}$ ${\displaystyle \mathbb {F} =({\mathcal {F}}_{t})_{t\in T}}$

${\displaystyle {\mathcal {F}}_{t}^{+}:=\bigcap _{s>t}{\mathcal {F}}_{s}{\text{ und }}\mathbb {F} ^{+}:=({\mathcal {F}}_{t}^{+})_{t\in T}}$.

Then applies

• The minimum is a stop time. ${\displaystyle \sigma \wedge \tau }$ ${\displaystyle \mathbb {F} }$
• The maximum is a stop time. ${\displaystyle \sigma \vee \tau }$ ${\displaystyle \mathbb {F} }$
• ${\displaystyle \sup _{j}\tau _{j}}$is a stop time. ${\displaystyle \mathbb {F} }$
• ${\displaystyle \sigma +a}$is a stop time, where is a fixed constant. ${\displaystyle \mathbb {F} }$ ${\displaystyle a\geq 0}$
• ${\displaystyle \sigma +\tau }$is a stop time. ${\displaystyle \mathbb {F} }$
• ${\displaystyle \inf _{j}\tau _{j}}$is a stop time. ${\displaystyle \mathbb {F} ^{+}}$
• ${\displaystyle \limsup _{j}\tau _{j}}$is a stop time. ${\displaystyle \mathbb {F} ^{+}}$
• ${\displaystyle \liminf _{j}\tau _{j}}$is a stop time. ${\displaystyle \mathbb {F} ^{+}}$

Web links

• Stopping time . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).

literature

• Heinz Bauer : Probability Theory , de Gruyter Textbook, 2002, ISBN 3-11-017236-4
• Achim Klenke: Probability Theory . 3. Edition. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6 , doi : 10.1007 / 978-3-642-36018-3 .
• Christian Hesse : Applied Probability Theory , Vieweg + Teubner-Verlag, Wiesbaden 2003, ISBN 3-528-03183-2 , doi : 10.1007 / 978-3-663-01244-3

Individual evidence

1. ↑ TO Shiryaev: Markov moment . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).