Froude and Rankine's theorem

In fluid mechanics , Froude and Rankine's theorem states that the flow velocity in the plane of rotation of a rotor , propeller or turbine can be expressed as the mean value of the flow velocities sufficiently far upstream and downstream. This statement goes back to Robert Edmund Froude and William John Macquorn Rankine .

Assumptions

Some assumptions are made for the derivation:

• horizontal flow ( potential energy is not considered)
• one-dimensional flow
• Turbine is projected onto a surface for simplification (no expansion downstream)
• infinite pressure gradient in the projection surface (jump in the pressure curve)
• incompressible fluid
• Dissipation is neglected
• stationary flow
• at a great distance from the projection surface the pressure has a constant value

Derivation

Schematic flow pattern around a wind turbine

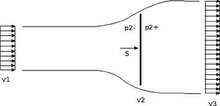
The starting point is the calculation of the thrust force on a circular area against which the flow occurs. The thrust can be determined in two ways. On the one hand from the difference in momentum change:

${\displaystyle S={\dot {m}}\cdot (v_{1}-v_{3})}$

which using the continuity equation to

${\displaystyle S=\rho \cdot v_{2}\cdot A\cdot (v_{1}-v_{3})}$

and on the other hand from energetic considerations in the form of the Bernoulli equations . In the latter case, two flow tubes are examined. One is placed from the beginning of the control area to immediately in front of the cross-section to be examined (index 2-). The second begins immediately after the cross-section and extends to the end of the calculation area (index 2+). Each of the two equations is converted to the pressure term in the immediate vicinity of cross-section 2. Due to the continuity equation , the flow velocities and are equal, so that after subtracting the second from the first equation, a pressure difference can be formed in the following form: ${\displaystyle v_{2-}}$ ${\displaystyle v_{2+}}$

${\displaystyle p_{2-}-p_{2+}={\frac {\rho }{2}}\cdot (v_{1}^{2}-v_{3}^{2})}$.

This pressure difference multiplied by the cross-section results in a force exerted by the flow on the rotor:

${\displaystyle S=A\cdot {\frac {\rho }{2}}\cdot (v_{1}^{2}-v_{3}^{2})}$.

Equating and rearranging the equations yields:

${\displaystyle v_{2}={\frac {1}{2}}\cdot (v_{1}+v_{3})}$.

application

The theorem is needed , for example, to derive the Betz coefficient for wind turbines.

Individual evidence

1. ↑ General Aviation Aircraft Design: Applied Methods and Procedures, Gudmundsson, S., 2013, ISBN 9780123973290