Topos (mathematics)

Topos (pl. Topoi , Greek place ) is a concept of category theory that occurs in two closely related forms, namely

• as an elementary topos , which is a generalized category of all sets , with the aim of a non-set theoretical foundation of mathematics.
• as a Grothendieck topos , which is a generalized topological space and has applications in algebraic geometry .

Elementary topos

motivation

The idea of ​​an elementary topos originally goes back to William Lawvere , who in 1963 set himself the goal of putting mathematics on a purely category-theoretical foundation (instead of the set theory that is still common today). In collaboration with Myles Tierney , he finally formulated the axioms for an elementary topos towards the end of the 1960s. Put simply, this is a kind of universe (informally speaking) in which it is possible to do mathematics. An elementary topos contains enough structure to define an abstract concept of a set and thus to operate mathematics and logic. In particular, an elementary topos has a so-called internal logic, which does not necessarily have to be classic .

definition

An elementary topos is a category with ${\displaystyle {\mathcal {E}}}$

• (a) a pullback for each chart ; ${\displaystyle A\to X\leftarrow B}$
• (b) a terminal object ; ${\displaystyle 1}$
• (c) an object , called the Sub-Object classifier (. literally of engl subobject classifier ) and a Monomorphismus so that for each Monomorphismus a unique arrow (called the character ) exist, so that the following diagram is a pullback: ${\displaystyle \Omega }$ ${\displaystyle \mathrm {true} \colon 1\rightarrowtail \Omega }$ ${\displaystyle m\colon A\rightarrowtail B}$ ${\displaystyle \chi _{m}\colon B\to \Omega }$ ${\displaystyle m}$

where here denotes the unique arrow from into the terminal object; ${\displaystyle !\colon A\to 1}$ ${\displaystyle A}$ ${\displaystyle 1}$

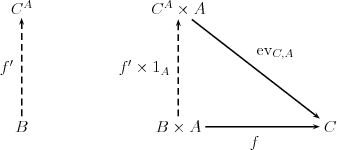
• (d) an exponential with an associated evaluation arrow for two objects each , with the universal property that there is exactly one arrow for each object and each arrow , so that the following diagram commutes: ${\displaystyle C^{A}}$ ${\displaystyle \mathrm {ev} _{C,A}:C^{A}\times A\to C}$ ${\displaystyle A,C}$ ${\displaystyle B}$ ${\displaystyle f\colon B\times A\to C}$ ${\displaystyle f'\colon B\to C^{A}}$

where denotes the identity arrow of . ${\displaystyle 1_{A}\colon A\to A}$ ${\displaystyle A}$

Properties (a) and (b) can be briefly summarized by saying is finitely complete (i.e. all finite limits exist). Properties (c) and (d) seem extremely artificial and abstract at first, but are both motivated by the category of all sets. In short, one often writes for (d) that the functor has a right adjoint (usually denoted by) for all of them . ${\displaystyle {\mathcal {E}}}$ ${\displaystyle \mathbf {Sets} }$ ${\displaystyle -\times A\colon {\mathcal {E}}\to {\mathcal {E}}}$ ${\displaystyle A}$ ${\displaystyle (-)^{A}}$

The original definition of an elementary topos also contained the requirement that it should be finite co-complete (i.e. that all finite colimites exist). This demand follows, however, after a non-trivial result by Mikkelsen.

Elementary topos as an abstraction of the category of all sets

As already said, a category-theoretical foundation for mathematics should be laid with the help of topo theory. This means in particular that the category of all quantities must be described by it. Accordingly, this is probably the most important example as far as the motivation of the various concepts of topo theory is concerned. In is simply the set of all images from to and according to . Further is (note that here is to be understood as a finite ordinal number), and the usual characteristic function of as a subset of . ${\displaystyle \mathbf {Sets} }$ ${\displaystyle \mathbf {Sets} }$ ${\displaystyle C^{A}=\{f\colon A\to C\}}$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle \mathrm {ev} _{C,A}\colon C^{A}\times A\to C,(f,a)\mapsto f(a)}$ ${\displaystyle \Omega =\{0,1\}=2}$ ${\displaystyle 2}$ ${\displaystyle \mathrm {true} :\{0\}\to \{0,1\},0\mapsto 1}$ ${\displaystyle \chi _{m}\colon B\to \{0,1\},b\mapsto \left\{{\begin{array}{ll}0&b\notin A\\1&b\in A\end{array}}\right.}$ ${\displaystyle A}$ ${\displaystyle B}$

The property that it contains only two elements means that it is a so-called boolean topos and is elementary for classical mathematics (classical in the sense of non-intuitionistic ). ${\displaystyle \Omega }$ ${\displaystyle \mathbf {Sets} }$

In order to distinguish abstract against general elementary topoi, the following axioms are usually used. ${\displaystyle \mathbf {Sets} }$

• There is an initial object (nontriviality). ${\displaystyle 0\not \cong 1}$
• If there are arrows, then there is or there is a with (well-dottedness). ${\displaystyle f,g\colon X\to Y}$ ${\displaystyle f=g}$ ${\displaystyle x\colon 1\to X}$ ${\displaystyle f\circ x\neq g\circ x}$
• There is an object of natural numbers ; H. an object along with arrows ${\displaystyle N}$

${\displaystyle 1{\stackrel {z}{\longrightarrow }}N{\stackrel {s}{\longrightarrow }}N,}$

so that for every object with arrows there is a clearly defined arrow with and . ${\displaystyle X}$ ${\displaystyle 1{\stackrel {x}{\longrightarrow }}X{\stackrel {f}{\longrightarrow }}X}$ ${\displaystyle h\colon N\to X}$ ${\displaystyle h\circ z=x}$ ${\displaystyle h\circ s=f\circ h}$

• For each epimorphism there is an arrow with ( axiom of choice ). ${\displaystyle e\colon X\to Y}$ ${\displaystyle m\colon Y\to X}$ ${\displaystyle e\circ m=1_{Y}}$

Grothendieck topos

A Grothendieck topos is defined as a category that is equivalent to the category of sheaves (of sets) on a situs . According to a theorem of Jean Giraud , a category is a Grothendieck topos if and only if the following properties are met: ${\displaystyle {\mathcal {E}}}$

• (a) In exist finite projective limits . ${\displaystyle {\mathcal {E}}}$
• (b) There are arbitrary co-products in and they are universally disjoint. ${\displaystyle {\mathcal {E}}}$

A coproduct is called disjoint if the structural morphisms are monomorphisms and is for an initial object. The coproduct is called universally disjoint if it remains disjoint under every change of base , that is, if it is disjoint. ${\displaystyle \textstyle S=\coprod _{i}S_{i}}$ ${\displaystyle S_{i}\to S}$ ${\displaystyle S_{i}\times _{S}S_{j}}$ ${\displaystyle i\neq j}$ ${\displaystyle T\to S}$ ${\displaystyle \textstyle T=\coprod _{i}(T\times _{S}S_{i})}$

• (c) Equivalence relations in are universally effective. ${\displaystyle {\mathcal {E}}}$

An equivalence relation is a pair of morphisms so that for each object the induced mapping is a bijection on the graph of an equivalence relation . It is . ${\displaystyle p_{1},p_{2}\colon R\to X}$ ${\displaystyle T\in \mathrm {Ob} ({\mathcal {E}})}$ ${\displaystyle (p_{1},p_{2})\colon R(T)\to X(T)\times X(T)}$ ${\displaystyle X(T)}$ ${\displaystyle X(T):=\operatorname {Hom} (T,X)}$

• (d) has a generating family of objects. ${\displaystyle {\mathcal {E}}}$

A family of objects is called generating if a morphism , for which all induced images are bijections, is an isomorphism. ${\displaystyle (E_{i})_{i\in I}}$ ${\displaystyle X\to Y}$ ${\displaystyle X(E_{i})\to Y(E_{i})}$

It should be noted that every Grothendieck topos is always an elementary topos.

literature

• Michael Artin , Alexander Grothendieck, Jean-Louis Verdier : Séminaire de géométrie algébrique du Bois-Marie. Théorie des topos et cohomologie étale des schémas. (SGA 4) 1963-64. SGA
• Francis Borceux: Handbook of Categorical Algebra 3: Categories of Sheaves . Cambridge, 1994.
• Rob Goldblatt: Topoi: the categorial analysis of logic. 1st edition. Amsterdam 1979. 2nd edition. Mineola NY 1984. Dover Publications, 2006, ISBN 0-486-45026-0 , Zbl 0434.03050 ( crit. Reviewed by Johnstone) Scans
• William Lawvere , Robert Rosebrugh: Sets for Mathematics . Cambridge University Press, 2003.
• Saunders Mac Lane , Ieke Moerdijk : Topos theory. In: M. Hazewinkel (Ed.): Handbook of algebra. Amsterdam 1996, ISBN 0-444-82212-7 , Volume I, pp. 501-528, Zbl 0858.18001
• Saunders Mac Lane, Ieke Moerdijk: Sheaves in geometry and logic: a first introduction to topos theory. Universitext, Berlin 1992, ISBN 0-387-97710-4 . xii, 627 p., Zbl 0822.18001
• Michael Barr , Charles Frederick Wells : Toposes, Triples and Theories.  - Berlin, 1983 (Basic Teachings of Math. Sciences; 278) cwru.edu
• Peter T. Johnstone : Sketches of an Elephant: A Topos Theory Compendium. Oxford Logic Guides, 43 & 44, 2002, ISBN 0-19-852496-X , Zbl 1071.18002
• Ieke Moerdijk, Jacob Johan Caspar Vermeulen: Proper Maps of Toposes. In: Mem. Am. Math. Soc. , 705, 2000, ISBN 0-8218-2168-7 , Zbl 0961.18003

Individual evidence

1. ↑ Robert Paré: Colimits in topoi . In: Bull. Amer. Math. Soc. , 80, 1974, pp. 556-561.
2. ^ Colin McLarty: Elementary Categories, Elementary Toposes . Oxford University Press, 2005, ISBN 0-19-851473-5 , pp. 211.213 .