Goat problem (geometry)

The goat problem in the unit circle

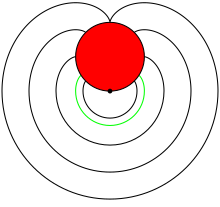
The goat problem - also known as the goat grazing - has been a problem in entertainment math that has been known since the 18th century . It was first published in 1748 in The Ladies Diary: or, the Woman's Almanack, which appears once a year in England .

Problem

How big must be in the illustration shown so that the red area is half of the circular area? Concrete motivation: A goat (or another animal) is tied to the point. How long does the leash have to be so that the animal can graze on exactly half of the circle? ${\displaystyle r}$ ${\displaystyle Q}$

Solution with calculation of the lens area

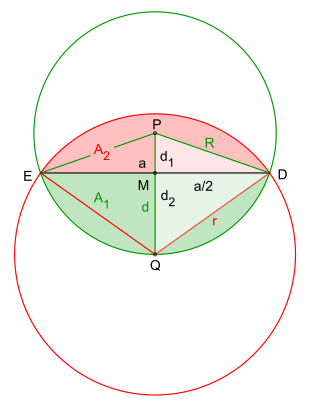
The area that the animal can reach has the shape of an asymmetrical lens (see calculation sketch ), which is delimited by two circular arcs .

In order to determine the area of the area bounded by the two circular arcs, this can be divided into two circular segments , the dividing line ending at the two intersection points and the circular arcs. With is the radius of the circle that represents the meadow and with that of the circle whose center lies on the edge of the circle of the other, and with is the distance between the two circle centers and . ${\displaystyle A}$ ${\displaystyle a}$ ${\displaystyle D}$ ${\displaystyle E}$ ${\displaystyle R}$ ${\displaystyle r}$ ${\displaystyle Q}$ ${\displaystyle d}$ ${\displaystyle P}$ ${\displaystyle Q}$

Heights and the right triangles MDP and DMQ, respectively ${\displaystyle d_{1}}$ ${\displaystyle d_{2}}$

Calculation sketch The grazing goat

Given: as well as ${\displaystyle R}$ ${\displaystyle d=d_{1}+d_{2}}$

According to the Pythagorean theorem:

${\displaystyle {\begin{aligned}(1)\;\;R^{2}={}&d_{1}^{2}+\left({\frac {a}{2}}\right)^{2}\;\;\Rightarrow \;\;(1.1)\;\left({\frac {a}{2}}\right)^{2}=R^{2}-d_{1}^{2}\\(2)\;\;\;r^{2}={}&\left(d-d_{1}\right)^{2}+\left({\frac {a}{2}}\right)^{2},\end{aligned}}}$

${\displaystyle \left({\frac {a}{2}}\right)^{2}}$of in results used ${\displaystyle \left(1.1\right)}$ ${\displaystyle \left(2\right)}$

${\displaystyle \;\left(3\right)\;\;r^{2}=\left(d-d_{1}\right)^{2}+R^{2}-d_{1}^{2},}$

multiplied out and rearranged results

${\displaystyle \;\left(4\right)\;\;r^{2}-R^{2}=d^{2}-2d\cdot d_{1},}$

results from it ${\displaystyle d_{1}}$

${\displaystyle \;\left(5\right)\;\;d_{1}={\frac {d^{2}-r^{2}+R^{2}}{2d}},}$

because of is supplemented accordingly ${\displaystyle d=d_{1}+d_{2}}$ ${\displaystyle \left(5\right)}$

${\displaystyle \;\left(6\right)\;\;d={\frac {d^{2}-r^{2}+R^{2}}{2d}}+{\frac {d^{2}+r^{2}-R^{2}}{2d}},}$

because of eventually surrenders ${\displaystyle d_{2}=d-d_{1}}$

${\displaystyle \;\left(7\right)\;\;d_{2}={\frac {d^{2}+r^{2}-R^{2}}{2d}}.}$

radius ${\displaystyle r}$

By applying the formula twice for the area of ​​a segment of a circle with the distance from the center of the circle or up to the chord ${\displaystyle d}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle a}$

${\displaystyle \;\left(8\right)\;\;A=R^{2}\cos ^{-1}\left({\frac {d}{R}}\right)-d{\sqrt {\left(R-d\right)\left(R+d\right)}}}$

and the terms of and from used therein, after appropriate reformulation, the formula for the area of ​​the asymmetrical lens is obtained: ${\displaystyle d_{1}}$ ${\displaystyle (5)}$ ${\displaystyle d_{2}}$ ${\displaystyle (7),}$

${\displaystyle {\begin{aligned}(9)\;\;A={}&A_{1}\left(R,d_{1}\right)+A_{2}\left(r,d_{2}\right)\\={}&R^{2}\cos ^{-1}\left({\frac {d^{2}-r^{2}+R^{2}}{2dR}}\right)+r^{2}\cos ^{-1}\left({\frac {d^{2}+r^{2}-R^{2}}{2dr}}\right)\;-\\&{}{\frac {1}{2}}{\sqrt {(d-r+R)(d+r+R)(d+r-R)(-d+r+R)}}\,.\end{aligned}}}$

For and half a circular area this is simplified to ${\displaystyle R=d=1}$

${\displaystyle \;\left(10\right)\;{\frac {1}{2}}\pi =\cos ^{-1}\left(1-{\frac {1}{2}}r^{2}\right)+r^{2}\cos ^{-1}\left({\frac {1}{2}}r\right)-{\frac {1}{2}}r{\sqrt {4-r^{2}}}.}$

This equation can only be solved numerically and results in (sequence A133731 in OEIS ). ${\displaystyle r=1{,}1587284\ldots }$

Solution with integration

From the integration over the right half of the lens surface with

${\displaystyle {\frac {1}{4}}\pi =\int _{0}^{\sqrt {r^{2}-{\frac {r^{4}}{4}}}}\left({\sqrt {r^{2}-t^{2}}}+{\sqrt {1-t^{2}}}-1\right)\,\mathrm {d} t}$

the also transcendent equation results

${\displaystyle r={\frac {\pi }{\pi r-{\sqrt {4-r^{2}}}+\left({\frac {4}{r}}-2r\right)\sin ^{-1}\left({\frac {1}{2}}r\right)}}}$

with the same solution.

Geometric approximation

The grazing goat ,
with an approximation of half the meadow area (green). Line length,
${\displaystyle r=}$ ${\displaystyle |AQ|={\sqrt {2}},}$ ${\displaystyle {\overline {BC}}=1}$

It starts with the unit circle around the point and the drawing in two mutually perpendicular standing radii ; this results in the intersection points and then the distance from is lengthened by about half a radius. This is followed by an arc around the point and down to the extended section, this results in the intersection. Now a short arc with the radius is drawn around ; it results in the intersection point. The subsequent connection of the point with creates the right-angled triangle with the desired radius as a hypotenuse. Finally, a circular arc around the point by defeat, the unit circle in and cuts. Thus, the circular area is roughly halved or, in other words, with a line length that is equal to the length , the goat can graze almost half of the meadow area. ${\displaystyle P}$ ${\displaystyle A}$ ${\displaystyle Q.}$ ${\displaystyle {\overline {AP}}}$ ${\displaystyle P}$ ${\displaystyle A}$ ${\displaystyle Q}$ ${\displaystyle {\overline {AP}};}$ ${\displaystyle B.}$ ${\displaystyle 1}$ ${\displaystyle B}$ ${\displaystyle C.}$ ${\displaystyle C}$ ${\displaystyle Q}$ ${\displaystyle QCP}$ ${\displaystyle r}$ ${\displaystyle Q}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle E}$ ${\displaystyle r}$

The picture opposite or the design description above shows:

${\displaystyle {\overline {AB}}={\sqrt {2}};\;\;{\overline {BC}}=1,}$

Therefore

${\displaystyle {\overline {BP}}={\overline {AC}}={\sqrt {2}}-1,}$

from this follows for the small leg of the right triangle ${\displaystyle QCP}$

${\displaystyle {\overline {PC}}={\sqrt {2}}-2\cdot \left({\sqrt {2}}-1\right),}$

according to the Pythagorean theorem, the following applies to the hypotenuse : ${\displaystyle r}$

${\displaystyle r={\sqrt {1+\left({\sqrt {2}}-2\cdot \left({\sqrt {2}}-1\right)\right)^{2}}}=1{,}1589416\ldots }$ [LE].

Absolute error in the constructed length of the line; where the radius corresponds to the numerically solved one (see above). ${\displaystyle r}$ ${\displaystyle r_{n}}$ ${\displaystyle r}$

${\displaystyle F_{r}=r-r_{n}=1{,}1589416-1{,}1587284=0,0002132}$ [LE]

The following applies to the relative error of the constructed radius : ${\displaystyle r}$

${\displaystyle f_{r}=\left({\frac {r_{n}}{r}}-1\right)\cdot 100\,\%,}$

with the values ​​used results

${\displaystyle f_{r}=\left({\frac {1{,}1587284}{1{,}1589416}}-1\right)\cdot 100\,\%\approx -0{,}018\,\%.}$

Inserting the radius into the simplified formula of the lens area for the unit circle (with ), described above in the solution with calculation of the lens area , results in approximately the constructed half of the meadow area, green in the picture ${\displaystyle r}$ ${\displaystyle R=d=1}$

${\displaystyle {A_{k}=1{,}1589416^{2}\cdot \cos ^{-1}\left({\frac {1}{2}}\cdot 1{,}1589416\right)+\cos ^{-1}\left(1-{\frac {1}{2}}\cdot 1{,}1589416^{2}\right)-{\frac {1}{2}}\cdot 1{,}1589416\cdot {\sqrt {4-1{,}1589416^{2}}}=1{,}571266696\ldots }}$ [FE].

Area of ​​half a meadow (half unit circle)

${\displaystyle A_{W}={\frac {\pi }{2}}=1{,}570796326\ldots }$ [FE]

Absolute error of the almost constructed half of the meadow area

${\displaystyle F_{A_{k}}=A_{k}-A_{W}=1{,}571266696-1{,}570796326=0{,}00047037}$ [FE]

Relative error of the approximately constructed half of the meadow area

${\displaystyle f_{A_{k}}=\left({\frac {1{,}570796326}{1{,}571266696}}-1\right)\cdot 100\,\%\approx -0{,}03\,\%}$

Example for clarification

If the circular meadow had the same radius then the line would be about too long and the goat - tied at the point to a line with the length - could also graze in addition to the half of the meadow area intended for it (round ) . ${\displaystyle 100\;\mathrm {m} ,}$ ${\displaystyle 2\;\mathrm {cm} }$ ${\displaystyle Q}$ ${\displaystyle 115{,}89\;\mathrm {m} }$ ${\displaystyle 15.708\;\mathrm {m} ^{2}}$ ${\displaystyle 4{,}7\;\mathrm {m} ^{2}}$

Extensions

The goat in space

The three-dimensional case with a unit ball above and a goat ball below

In the three-dimensional case, there is a point on the surface of a unit sphere , and the question is how large the radius of the second sphere must be so that the intersection body has exactly half the volume of the unit sphere. ${\displaystyle Q}$ ${\displaystyle r}$

The part of the unit sphere that the animal can reach has the shape of a three-dimensional lens with differently curved sides, which is delimited by the two spherical caps .

The volume of a lens with two spheres with radii and center distance is: ${\displaystyle V}$ ${\displaystyle R,r}$ ${\displaystyle d}$

${\displaystyle V={\frac {\pi (R+r-d)^{2}\left(d^{2}+2dr-3r^{2}+2dR+6rR-3R^{2}\right)}{12d}}}$

which is simplified to at and half the volume of the sphere ${\displaystyle R=d=1}$

${\displaystyle {\frac {1}{2}}\cdot {\frac {4}{3}}\pi =-{\frac {1}{4}}\pi r^{4}+{\frac {2}{3}}\pi r^{3}}$

from which follows as a solution ${\displaystyle r=1{,}2285\ldots }$

It can be shown that the value approaches as the dimensionality increases . ${\displaystyle r}$ ${\displaystyle {\sqrt {2}}}$

The goat at the silo

The goat outside the circle

The Monty Hall problem with silo for cable lengths of , , , and (green) ${\displaystyle {\tfrac {1}{4}}\cdot \pi r}$ ${\displaystyle {\tfrac {1}{2}}\cdot \pi r}$ ${\displaystyle {\tfrac {3}{4}}\cdot \pi r}$ ${\displaystyle 1\cdot \pi r}$ ${\displaystyle 1\cdot r}$

In the two-dimensional case, the question of the size of the achievable area outside the red circle can also be asked. This corresponds to the situation that the animal is tied to a silo.

In this case the area consists of a semicircle (light blue) with a radius and two areas that are delimited by the red circle and the involute of a circle (dark blue). The content of one of the dark blue areas follows from Leibniz's sector formula . The total achievable area (light and dark blue) is then ${\displaystyle r}$

${\displaystyle A={\frac {1}{2}}\pi r^{2}+{\frac {1}{3}}r^{3}}$

on condition that (otherwise the two dark blue areas on the back of the silo overlap). ${\displaystyle r\leq \pi }$

See also

• Goat problem

literature

• Raymond Clare Archibald : Involutes of a circle and a pasturage problem. In: American Mathematical Monthly , 28, 1921, pp. 328-329.
• Marshall Fraser: A tale of two goats. In: Mathematics Magazine , 55, 1982, pp. 221-227.
• Jean Jacquelin: The problem of the hyperchevre. In: Quadrature , 49, 2003, ISSN  1142-2785 , pp. 6-12.

Individual evidence

1. ↑ Heinrich Hemme : The hell of numbers. 92 math puzzles with detailed solutions . Vandenhoeck & Ruprecht, Göttingen 2007, ISBN 978-3-525-40841-4 , p. 32 and 102 f .
2. ↑ ^{a b} Eric Weisstein: Goat Problem. WolframMathworld, accessed November 17, 2019 . 
3. ^ ^{A b c} Eric Weisstein: Circle-Circle Intersection. WolframMathworld, accessed November 17, 2019 . 
4. ↑ Eric Weisstein: Circular Segment. WolframMathworld, accessed November 17, 2019 .