Approximation of the one

An approximation of one is a term from the mathematical theory of Banach algebras . Many Banach algebras that are important for applications do not have a unit element . An adjunct of a single element would usually be an unnatural approach. In such situations, however, the approximations of one to be discussed here may be present; these then form a substitute for the missing one element.

According to examples for Banach algebras without one element, approximations of one are defined. Finally, approximations of one are given for the examples mentioned.

Examples of Banach algebras without a unit element

• Let be a locally compact Hausdorff space . The C * -algebra of continuous functions that vanish at infinity only has a unit element if is compact. In this case the constant function 1 is the one element. The C * algebra has no unit element. ${\displaystyle X}$ ${\displaystyle C_{0}(X)}$ ${\displaystyle f:X\rightarrow \mathbb {C} }$ ${\displaystyle X}$ ${\displaystyle C_{0}(\mathbb {R} )}$
• Be a locally compact group . Then the convolution algebra L ¹ (G) has a unity if and only if is discrete . In this case, for all , is the one element (where is the neutral element of the group). The algebra examined in the context of the Fourier transformation has no unity element. ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle \delta _{e}:G\rightarrow \mathbb {C} ,\,\delta _{e}(e)=1,\delta _{e}(g)=0}$ ${\displaystyle g\not =e}$ ${\displaystyle e}$ ${\displaystyle L^{1}(\mathbb {R} )}$
• The C * -algebra of compact operators , the trace class and the Hilbert-Schmidt class over a Hilbert space have a unit element if and only if the dimension of is finite. In this case the identical mapping is the single element. In the cases important for applications or , there are no single elements. ${\displaystyle H}$ ${\displaystyle H}$ ${\displaystyle 1_{H}}$ ${\displaystyle H=\ell ^{2}}$ ${\displaystyle H=L^{2}(\mathbb {R} )}$
• The sequence spaces , are the component-wise multiplication Banach without identity. ${\displaystyle \ell ^{p},\,1\leq p<\infty }$

Definitions

A left approximation of one (or right approximation of one ) of a Banach algebra is a network with (or ) for all . ${\displaystyle A}$ ${\displaystyle (e_{i})_{i\in I}}$ ${\displaystyle e_{i}a{\stackrel {i\in I}{\longrightarrow }}a}$ ${\displaystyle ae_{i}{\stackrel {i\in I}{\longrightarrow }}a}$ ${\displaystyle a\in A}$

A (two-sided) approximation of one is a network that is both left and right approximation of one.

Properties of the network, such as B. Countability or boundedness are also assigned to the approximations of one.

If there is a one-element , the one-element network is an approximation of one. Banach algebras with an approximation of one thus generalize Banach algebras with one element. ${\displaystyle A}$ ${\displaystyle e}$ ${\displaystyle (e)}$

Bounded approximations of one

If there is a bounded left approximation of one and a bounded right approximation of one , then one can show by a simple calculation that a bilateral bounded approximation is one. ${\displaystyle A}$ ${\displaystyle (e_{i})_{i\in I}}$ ${\displaystyle (f_{j})_{j\in J}}$ ${\displaystyle (e_{i}+f_{j}-f_{j}e_{i})_{(i,j)\in I\times J}}$

A Banach space that is a - left module is called a Banach - left module if there is a constant with for all and . An important special case is with the Banach algebra product as a module operation. ${\displaystyle X}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle k>0}$ ${\displaystyle \|a\cdot x\|\leq k\|a\|\cdot \|x\|}$ ${\displaystyle a\in A}$ ${\displaystyle x\in X}$ ${\displaystyle X=A}$

If a Banach- left module, and has a bounded approximation of the one with for all , then one can factorize each via , that is, there is one and one with , in formulas . ${\displaystyle X}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle (e_{i})_{i}}$ ${\displaystyle e_{i}x\rightarrow x}$ ${\displaystyle x\in X}$ ${\displaystyle x\in X}$ ${\displaystyle A}$ ${\displaystyle a\in A}$ ${\displaystyle y\in X}$ ${\displaystyle x=ay}$ ${\displaystyle X=A\cdot X}$

The special case deserves special mention: If a Banach algebra with limited approximation of one, then , more precisely: every element in can be written as a product of two elements. ${\displaystyle X=A}$ ${\displaystyle A}$ ${\displaystyle A=A\cdot A}$ ${\displaystyle A}$

Examples

Zero multiplication

A Banach space different from 0 becomes a Banach algebra if the product of two elements is declared as 0. Such a Banach algebra cannot contain an approximation of one.

C * algebras

• Every C * algebra has an approximation of one bounded by 1.

With the help of the continuous functional calculus one can show that with respect to the order (see positive operator ) on the set of self-adjoint elements there is an upward set and therefore represents a network itself. This network is an approximation of one. ${\displaystyle \{x\in A;\,0\leq x,\|x\|\leq 1\}}$ ${\displaystyle \leq }$

In many cases, however, one can specify simpler networks (in the separable case even sequences). In the example above, let ${\displaystyle C_{0}(\mathbb {R} )}$

The sequence of functions forms an approximation of the one for . ${\displaystyle e_{n}\,}$ ${\displaystyle C_{0}(\mathbb {R} )}$

${\displaystyle e_{n}(x)={\begin{cases}1&{\mbox{wenn }}-n\leq x\leq n\\n+1+x,&{\mbox{wenn }}-(n+1)\leq x<-n\\n+1-x,&{\mbox{wenn }}n<x\leq n+1\\0,&{\mbox{sonst}}\end{cases}}}$.

Then the sequence is an approximation of the one in . ${\displaystyle (e_{n})_{n}}$ ${\displaystyle C_{0}(\mathbb {R} )}$

Group algebras

The sequence of functions forms an approximation of the one for . ${\displaystyle \phi _{n}\,}$ ${\displaystyle L^{1}(\mathbb {R} )}$

• If a locally compact group, then has an approximation of one bounded by 1. ${\displaystyle G}$ ${\displaystyle L^{1}(G)}$

Be a left Hair measure on . If there is a surrounding basis of the neutral element of , then for each there is a continuous function with a compact , in- located carrier , for all and . Since inclusion is directed as the environment base , there is a network that can be shown to be an approximation of the one for . ${\displaystyle \mu }$ ${\displaystyle G}$ ${\displaystyle {\mathcal {U}}}$ ${\displaystyle G}$ ${\displaystyle U\in {\mathcal {U}}}$ ${\displaystyle \phi _{U}:G\rightarrow \mathbb {R} _{0}^{+}}$ ${\displaystyle U}$ ${\displaystyle \phi _{U}(t)\,=\,\phi _{U}(t^{-1})}$ ${\displaystyle t\in G}$ ${\displaystyle \int _{G}\phi _{U}(t)\,{\rm {d}}\mu (t)=1}$ ${\displaystyle {\mathcal {U}}}$ ${\displaystyle (\phi _{U})_{U\in {\mathcal {U}}}}$ ${\displaystyle L^{1}(G)}$

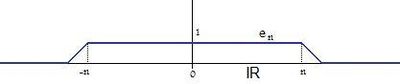
In the special case with the Lebesgue measure as a hair measure, the sequence of the quantities can be used as the environmental basis . One sets as follows ${\displaystyle G=\mathbb {R} }$ ${\displaystyle U_{n}=[-{\frac {1}{n}},{\frac {1}{n}}]}$ ${\displaystyle \phi _{n}=\phi _{U_{n}}}$

${\displaystyle \phi _{n}(x)={\begin{cases}n+n^{2}x&{\mbox{wenn }}-1/n\leq x<0\\n-n^{2}x,&{\mbox{wenn }}0\leq x<1/n\\0,&{\mbox{sonst}}\end{cases}}}$

so the sequence is an approximation of one for . You can also find differentiable functions as often as you like , which form an approximation of one, which plays a role in the theory of the Fourier transformation and the theory of distribution (approximation of the delta distribution ). ${\displaystyle (\phi _{n})_{n}}$ ${\displaystyle L^{1}(\mathbb {R} )}$ ${\displaystyle \phi _{n}}$

Operator algebras

Let it be the directed set of finite-dimensional subspaces of an infinite-dimensional Hilbert space , let it be the orthogonal projection onto . Then an approximation of one for the C * -algebra of the compact operators on is , even a bounded approximation of one, because orthogonal projections have the operator norm 1. ${\displaystyle {\mathcal {E}}}$ ${\displaystyle H}$ ${\displaystyle P_{E}}$ ${\displaystyle E}$ ${\displaystyle (P_{E})_{E\in {\mathcal {E}}}}$ ${\displaystyle C(H)}$ ${\displaystyle H}$

This network is also an approximation of the one in the shadow classes , especially in the track class and in the Hilbert-Schmidt class , but not restricted, because for the track norm to which the Hilbert-Schmidt norm applies , applies in general to the norm of the shadow class . One can show that there are no bounded approximations of one in the shadow classes. For the Hilbert-Schmidt class this follows from the above-mentioned theorem about Banach links modules, because . ${\displaystyle {\mathcal {S}}_{p}(H)}$ ${\displaystyle \|P_{E}\|_{1}={\mbox{dim}}(E)}$ ${\displaystyle \|P_{E}\|_{2}={\sqrt {{\mbox{dim}}(E)}}}$ ${\displaystyle \|P_{E}\|_{p}=({\mbox{dim}}(E))^{1/p}}$ ${\displaystyle {\mathcal {S}}_{2}(H)\cdot {\mathcal {S}}_{2}(H)={\mathcal {S}}_{1}(H)\not ={\mathcal {S}}_{2}(H)}$

swell

• FF Bonsall, J. Duncan: Complete Normed Algebras . Springer-Verlag 1973, ISBN 3540063862 .
• J. Dixmier : Les C * -algèbres et leurs représentations. , Gauthier-Villars, 1969, ISBN 9782876470132 .
• RV Kadison , JR Ringrose : Fundamentals of the Theory of Operator Algebras. 1983, ISBN 0123933013 .
• Gert K. Pedersen: C * -Algebras and Their Automorphism Groups. ISBN 0125494505 .