Daubechies wavelets

Under Daubechies wavelets , named after Ingrid Daubechies , is understood in the digital signal processing in a class of orthogonal wavelet - functions that a compact carrier have. They are among the wavelets that are most frequently used in practice and are used in wavelet transformations, for example for purposes of digital signal analysis and signal compression . Because they can be easily implemented using the fast wavelet transformation (FWT), they are also text (book) examples of digital signal processing.

description

In terms of functional analysis , the wavelet function, together with its integer shifts and the compression / expansion of these functions with powers of two as a factor, creates an orthonormal basis of the Hilbert space L² (IR) , i.e. That is, every square integrable function can be broken down into parts that look similar to the wavelet function. The Haar wavelet , a piece-wise constant function, had been known with this property since 1909 . Ingrid Daubechies is responsible for being the first to construct a continuous function with this property.

For every wavelet there are two finite sequences of real numbers that can be used as digital low-pass and high-pass filters in a filter bank that is part of the FWT. The length N of these filters, also referred to as the number of taps, is part of the designation D N of the individual Daubechies wavelets. In practice, the Daubechies wavelets with the designations D2-D20 are mostly used. For theoretical reasons, only N = 2A occur. Every wavelet of this class has the maximum number A of vanishing moments (in English literature "vanishing moments"), i. That is, the wavelet function is perpendicular (in the sense of L² (IR), i.e. the integral of the product of both functions is zero) to every polynomial with degree at most A − 1 . For example, D2 (the Haar wavelet ) has a vanishing moment and is perpendicular to all constant functions, D4 has two such moments and is perpendicular to all linear functions (which includes the constant functions), etc. The number A of vanishing moments is a measure the quality of a scaling function.

Ingrid Daubechies also introduced a class of biorthogonal wavelets with similar characteristics. These wavelets are no longer orthogonal, but they are symmetrical.

The orthogonal Daubechies wavelets

	A = 2, N = 4, carrier [0.3]	A = 6, N = 12, carrier [0.11]	A = 10, N = 20, carrier [0.19]
Scaling and wavelet functions
Amplitudes of their frequency spectrum

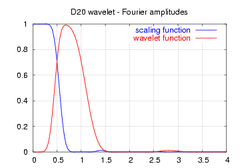
Algebraic Conditions

The scaling function in any multiscale analysis is the solution of a fractal functional equation called the refinement equation or two- scale equation:

${\displaystyle \phi (x)=\sum _{k=0}^{N-1}a_{k}\phi (2x-k)}$,

where the finite sequence of real numbers is called the scaling sequence or mask. The wavelet function results in a similar way as a linear combination ${\displaystyle (a_{0},\dots ,a_{N-1})}$

${\displaystyle \psi (x)=\sum _{k=0}^{M-1}b_{k}\phi (2x-k)}$,

with a suitable finite sequence of real numbers called a wavelet sequence or mask. ${\displaystyle (b_{0},\dots ,b_{M-1})}$

If the existence of a continuous solution of the refinement equation is known, an arbitrarily precise approximation of this can be found by setting up the finite-dimensional linear system of equations that must satisfy the values ​​of the scaling function at integer places. Since this system of equations is homogeneous, one adds the condition that the sum of these values ​​should be 1. The values ​​for the multiples of 1/2, from these the values ​​for the multiples of 1/4 etc. can be found by simply inserting the values ​​at the integer places. The same applies to the values ​​of the wavelet function. In this way the above diagrams were generated.

Orthogonal wavelets

This class of wavelets has the property that the scaling function together with its integer shifts in combination with the wavelet function with its integer shifts form an orthonormal system in the Hilbert space L² (IR) . For this orthogonality it is necessary that the scaling sequence is perpendicular to all even-numbered shifts of itself:

${\displaystyle \sum _{n\in \mathbb {Z} }a_{n}a_{n+2m}=2\delta _{m,0}}$.

In the orthogonal case, the coefficients of the wavelet sequence result directly from the coefficients of the scaling sequence

${\displaystyle b_{n}=(-1)^{n}a_{N-1-n}\qquad {\text{mit }}n=0,\ldots ,N-1}$

Sometimes the other sign is found in the literature.

Biorthogonal wavelets

The second class introduced by Ingrid Daubechies together with Albert Cohen and Jean-Christophe Feauveau are the biorthogonal wavelets . Although these do not have the above-mentioned orthogonality property, they only deviate slightly from it. To do this, they can be constructed in such a way that the scaling function is symmetric and the wavelet function is also symmetric or antisymmetric. However, a pair of generating functions is not sufficient here, rather two scaling functions are required , which can generate different multi- scale analyzes, and accordingly two different wavelet functions . The two scaling sequences must now fulfill the following biorthogonality condition for all integer m : ${\displaystyle \phi ,{\tilde {\phi }}}$ ${\displaystyle \psi ,{\tilde {\psi }}}$

${\displaystyle \sum _{n\in \mathbb {Z} }a_{n}{\tilde {a}}_{n+2m}=2\delta _{m,0}}$

If this is fulfilled, the wavelet sequences result as

${\displaystyle {\begin{alignedat}{2}b_{n}&=(-1)^{n}{\tilde {a}}_{M-1-n}&\qquad &\mathrm {f{\ddot {u}}r} \quad n=0,\ldots ,M-1\\{\tilde {b}}_{n}&=(-1)^{n}a_{M-1-n}&&\mathrm {f{\ddot {u}}r} \quad n=0,\ldots ,N-1\end{alignedat}}}$

where N is the length of the scaling sequence zu and M is the length of the scaling sequence zu . ${\displaystyle \phi }$ ${\displaystyle {\tilde {\phi }}}$

The Jpeg 2000 standard also uses the biorthogonal Daubechies 5/3 wavelet (also known as LeGall 5/3 wavelet) for lossless and the Daubechies 9/7 wavelet (also known as Cohen-Daubechies Feauveau ) for image compression 9/7 or "CDF 9/7" or FBI fingerprint wavelet known) for lossy compression.

Analytical conditions

Vanishing moments and polynomial approximation

A necessary condition for the existence of an r -fold continuously differentiable solution ( r = 0 for only continuous) of the refinement equation is that the polynomial (1 + Z) ^{r + 1} divides the generating function or Z-transformation of the scaling sequence a . The maximum power A such that (1 + Z) ^{A is} a factor of a (Z) is called the polynomial approximation order . It indicates the ability of the scaling function to represent polynomials up to degree A-1 as a linear combination of integer shifts of the scaling function . ${\displaystyle a(Z):=a_{0}+a_{1}Z+\dots +a_{N-1}Z^{N-1}}$ ${\displaystyle \phi }$

• In the biorthogonal case, an approximation order A of results in an equal number A of vanishing moments of the dual wavelet , which follows from the fact that (1 + Z) ^{A is} a factor of . Conversely, the approximation order à of is equal to the number à of vanishing moments of the wavelet . ${\displaystyle \phi }$ ${\displaystyle {\tilde {\psi }}}$ ${\displaystyle b(Z)=Z^{-1}a(-Z^{-1})}$ ${\displaystyle {\tilde {\phi }}}$ ${\displaystyle \psi }$
• In the orthogonal case, A and à match, as do and is. ${\displaystyle \phi ={\tilde {\phi }}}$ ${\displaystyle \psi ={\tilde {\psi }}}$

Smoothness of functions

A criterion for the solvability of refinement equation is the following: we factoring , a polynomial in with , and there is a barrier of the type ${\displaystyle a(Z)=2^{1-A}(1+Z)^{A}p(Z)}$ ${\displaystyle p}$ ${\displaystyle Z}$ ${\displaystyle p(1)=1}$

${\displaystyle 1\leq \sup _{t\in [0,2\pi ]}|p(e^{it})|<2^{A-1-r}}$for a , ${\displaystyle r\in \mathbb {N} }$

so the refinement equation has a -fold continuously differentiable solution with carrier in the interval , where . ${\displaystyle r}$ ${\displaystyle \left[0,N-1\right]}$ ${\displaystyle N=A+deg(p)+1}$

Examples

• ${\displaystyle a(Z):=2^{1-A}(1+Z)^{A}}$, which includes a constant . According to the above, it must apply, i. H. the solutions would be at least -fold continuously differentiable. In fact, the solutions are Schoenberg's B-splines of the order that have a -th piecewise constant derivative, in particular the -th derivative is Lipschitz continuous . The case that falls out of this treatment corresponds to the index function of the unit interval and is the scaling function of the Haar wavelet . ${\displaystyle p(Z)=1}$ ${\displaystyle n<A-1}$ ${\displaystyle A-2}$ ${\displaystyle A-1}$ ${\displaystyle (A-1)}$ ${\displaystyle (A-2)}$ ${\displaystyle A=1}$
• One can start in the case and linear . If we determine the monomial coefficients of this 3rd degree polynomial and insert these 4 coefficients into the orthogonality condition, then exactly the condition remains in the end . If we insert the positive root in , we get the scaling sequence of the D4 wavelet, see also the table below. ${\displaystyle A=2}$ ${\displaystyle p}$ ${\displaystyle a(Z)={\tfrac {1}{4}}(1+Z)^{2}\,((1+Z)+c(1-Z))}$ ${\displaystyle c_{2}=3}$ ${\displaystyle c}$

construction

The Daubechies wavelets correspond to the case of minimal degrees of freedom in determining the scaling sequences. On the one hand, the minimum length of the scaling sequence can be sought for a given number of vanishing moments, and on the other hand the maximum number of vanishing moments for a given length. The following applies in both cases . ${\displaystyle A}$ ${\displaystyle N}$ ${\displaystyle N=2A}$

Orthogonal wavelets

If we use the above factorization of the scaling sequence,, with , then the orthogonality conditions can also be summarized in a Laurent polynomial: ${\displaystyle a(Z)=2^{1-A}(1+Z)^{A}p(Z)}$ ${\displaystyle p(1)=1}$

${\displaystyle a(Z)a(Z^{-1})+a(-Z)a(-Z^{-1})=4\quad \Rightarrow \quad (1-u)^{A}p(Z)p(Z^{-1})=1-u^{A}\,[p(-Z)p(-Z^{-1})]}$

with the abbreviation . From this equation it can be deduced that it cannot work, so at least what follows in the minimal case applies . ${\displaystyle u:=1/4\cdot (2-Z-Z^{-1})}$ ${\displaystyle degp<A-1}$ ${\displaystyle degp=A-1}$ ${\displaystyle N=2a}$

We can multiply with the inverse power series and break off at the power , ${\displaystyle (1-u)^{A}}$ ${\displaystyle u^{A}}$

${\displaystyle p(Z)p(Z^{-1})=\sum _{k=0}^{A-1}{\binom {-A}{k}}(-u)^{k}=\sum _{k=0}^{A-1}{\binom {A+k-1}{k}}u^{k}}$.

This equation is solvable, its solutions result from a method called spectral factorization . First, the zeros on the right-hand side are determined as a polynomial in . This results in quadratic equations with mutually reciprocal solutions, one of which is assigned. Therefore, there are possible solutions, you can z. B. opt for the one in which all zeros are inside or outside of the unit circle. ${\displaystyle u}$ ${\displaystyle A-1}$ ${\displaystyle Z}$ ${\displaystyle p(Z)}$ ${\displaystyle 2^{A-1}}$ ${\displaystyle p(Z)}$

The following table shows the resulting scaling sequences for the wavelets D2-D20, i. H. for until , listed. ${\displaystyle A=1}$ ${\displaystyle A=10}$

Orthogonal Daubechies coefficients

D2 ( hair )	D4	D6	D8	D10	D12	D14	D16	D18	D20
1	0.6830127	0.47046721	0.32580343	0.22641898	0.15774243	0.11009943	0.07695562	0.05385035	0.03771716
1	1.1830127	1.14111692	1.01094572	0.85394354	0.69950381	0.56079128	0.44246725	0.34483430	0.26612218
	0.3169873	0.650365	0.8922014	1.02432694	1.06226376	1.03114849	0.95548615	0.85534906	0.74557507
	−0.1830127	−0.19093442	−0.03967503	0.19576696	0.44583132	0.66437248	0.82781653	0.92954571	0.97362811
		−0.12083221	−0.26450717	−0.34265671	−0.31998660	−0.20351382	−0.02238574	0.18836955	0.39763774
		0.0498175	0.0436163	−0.04560113	−0.18351806	−0.31683501	−0.40165863	−0.41475176	−0.35333620
			0.0465036	0.10970265	0.13788809	0.1008467	6.68194092e − 4	−0.13695355	−0.27710988
			−0.01498699	−0.00882680	0.03892321	0.11400345	0.18207636	0.21006834	0.18012745
				−0.01779187	−0.04466375	−0.05378245	−0.02456390	0.04345268	0.13160299
				4.71742793e − 3	7.83251152e − 4	−0.02343994	−0.06235021	−0.09564726	−0.10096657
					6.75606236e − 3	0.01774979	0.01977216	3.54892813e − 4	−0.04165925
					−1.52353381e − 3	6.07514995e − 4	0.01236884	0.03162417	0.04696981
						−2.54790472e − 3	−6.88771926e − 3	−6.67962023e − 3	5.10043697e − 3
						5.00226853e − 4	−5.54004549e − 4	−6.05496058e − 3	−0.01517900
							9.55229711e − 4	2.61296728e − 3	1.97332536e − 3
							−1.66137261e − 4	3.25814671e − 4	2.81768659e − 3
								−3.56329759e − 4	−9.69947840e − 4
								−5.5645514e − 5	−1.64709006e − 4
									1.32354367e − 4
									−1.875841e − 5

The wavelet coefficients can be derived by reversing the order and sign for every other coefficient. For D4 this would be e.g. B. -0.1830127, -0.3169873, 1.1830127, -0.6830127.

Biorthogonal symmetric wavelets

Closely related to the Daubechies wavelets are the Cohen-Daubechies-Feauveau wavelets (CDF wavelets). In contrast to the Daubechies wavelets, the latter are only orthogonal in pairs (biorthogonal), but symmetrical.

CDF wavelets became known because they are used in the JPEG 2000 standard. Furthermore, the wavelet used in the FBI's fingerprint database is a CDF wavelet.

See also

• Hair wavelet
• Wavelet compression
• Gauss-Laplace pyramid

literature

• Carlos Cabrelli, Ursula Molter: Generalized Self-Similarity . In: Journal of Mathematical Analysis and Applications. 230, 1999, pp. 251-260 ( PDF ).

Web links

• Ingrid Daubechies: Ten Lectures on Wavelets . SIAM 1992.
• Hardware implementation of wavelets
• wavelet.org , special reference is made to the "Gallery" with tutorial and book recommendations