Wavelet

In mathematics, the term wavelet describes a group of functions with a wave-like character. The word is a new creation from the French "ondelette" , which means " small wave " and was translated partly literally ("onde" → "wave"), partly phonetically ("-lette" → "-let") into English. Wavelets describe the basic function of a continuous or discrete wavelet transformation . The wavelet transformation is currently the main area of application for wavelet functions.

history

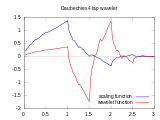
Wavelets have their origin in signal analysis and engineering. The term "wavelet" was coined in the 1980s in geophysics ( Jean Morlet , Alex Grossmann ) for functions that generalize the short-term Fourier transform , but has only been used since the late 1980s in the meanings customary today. In the 1990s, a real wavelet boom arose, triggered by the discovery of compact, continuous (up to any order of differentiability) and orthogonal wavelets by Ingrid Daubechies (1988) and the development of the fast wavelet transformation (FWT) algorithm. using the multiresolution analysis (multiresolution analysis - MRA) by Stephane Mallat and Yves Meyer (1989).

Wavelets and transformations

In contrast to the sine and cosine functions of the Fourier transformation , the most commonly used wavelets not only have locality in the frequency spectrum , but also in the time domain. "Locality" is to be understood in the sense of small spread . A sine or cosine function, for example, is not local in the time domain due to its periodicity. The probability density is the normalized square of the absolute value of the function under consideration or of its Fourier transform. The product of both variances is always greater than a constant, analogous to Heisenberg's uncertainty principle , see also the WKS sampling theorem . Out of this restriction, the Paley-Wiener theory ( Raymond Paley , Norbert Wiener ), a forerunner of the discrete wavelet transformation, and the Calderón-Zygmund theory ( Alberto Calderón , Antoni Zygmund ), which of the continuous wavelet Transformation corresponds.

The integral of a wavelet function is preferably 0, which is why the wavelet function usually takes the form of outwardly running out (becoming smaller) waves (ie "waves" = ondelettes = wavelets).

Hair wavelet
Daubechie's D4 wavelet
Daubechie's D20 wavelet

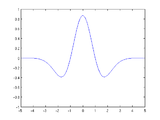
Important examples of wavelets are the Haar wavelet ( Alfréd Haar 1909), the Daubechies wavelets named after Ingrid Daubechies (around 1990), the Coiflet wavelets that she also constructed, and the more theoretically important Meyer wavelet ( Yves Meyer , around 1988 ).

Meyer wavelet
Morlet wavelet
Mexican hat

There are wavelets for spaces of any dimension, mostly a tensor product of a one-dimensional wavelet basis is used. Due to the fractal nature of the two-scale equation in the MRA, most wavelets are complex in shape, most are not closed in shape.

In the Anglo-Saxon language area, the English term " wavelet " is defined more broadly: There, wavelet is understood to be a wave-like oscillation with an amplitude beginning with zero, an amplitude increase and a subsequent amplitude decrease back to zero. One-dimensional wavelets with an integral other than zero are thus also included in this broader definition of the term wavelet. Such wavelets are used, for example, in certain digital signal processing methods . For example, distributions will be perceived as such a class of wavelets, which for example, the scanning can be performed of a signal. A particularly important example, which in this extended sense can be understood as the extreme form of a wavelet, is the Dirac delta function . The use of a specific wavelet transformation is therefore always linked to the use of a respectively associated wavelet subset for the wavelet transformation.

application

Wavelets are used in signal processing methods , especially signal compression , which contain a discrete wavelet transformation as the first step . These have been propagated as milestones in image compression and audio data compression since the early 1990s . Nevertheless, outside of special applications, such as B. in geophysics or computed tomography, such wavelet compression methods are only implemented in the JPEG2000 standard and its direct predecessors such as the DjVu and the LuraWave format. So far, JPEG2000 has not been widely used. In a broad sense, the common JPEG is also based on a wavelet transformation; the discrete cosine transformation used can be interpreted as a Haar wavelet . In methods of signal analysis, the continuous wavelet transformation is used in a discretized form.

Discrete wavelet transform wavelets

A wavelet is here the generating function of an affine system of functions which have a Hilbert basis , i. H. form a complete orthonormal system in the functional space. The representation of a function by means of these functions is called a wavelet transformation : ${\ displaystyle \ psi}$ ${\ displaystyle \ psi _ {j, k} (x): = 2 ^ {j / 2} \, \ psi (2 ^ {j} \, xk)}$ ${\ displaystyle L ^ {2} (\ mathbb {R})}$

{\ displaystyle f \ mapsto c (f): = {\ mathcal {W}} [f] = \ left (c_ {j, k} (f): = \ langle f, \, \ psi _ {j, k } \ rangle: \; j, k \ in \ mathbb {Z} \ right)}

and inverse wavelet transform

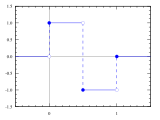
{\ displaystyle c = (c_ {j, k}: \; j, k \ in \ mathbb {Z}) \ mapsto {\ mathcal {W}} ^ {*} [f]: = \ sum _ {j, k \ in \ mathbb {Z}} c_ {j, k} \ cdot \ psi _ {j, k}}

.

The most elementary example is the Haar wavelet . It is helpful if the wavelet function is associated with a multiscale analysis , since in the practical calculation the evaluation of many of the integrals behind the scalar products can be replaced by repeated convolution of coefficient sequences with finite filter sequences that have been obtained. This accelerated procedure is called a correspondingly fast wavelet transformation .

Signal processing

The relationship between wavelets and filters for signal processing is now quite clear: The wavelet mask corresponds to the impulse response of a bandpass filter with a certain sharpness in time (filter length) and in frequency ( bandwidth ). Filter length and bandwidth are inversely proportional, so "stretching" the filter by a factor of 2 will halve the bandwidth.

Extensions

It is possible and useful to consider other scale factors. The DCT variant in the JPEG algorithm corresponds to a Haar wavelet with a block size of 8. Further weakening of the analytical requirements results in wavelet frames (see frame ) or frame sets , which generate a redundant signal transformation, which is preferable under certain circumstances Example of noise reduction.

A variant that has recently emerged are the so-called multiwavelets , which have not one, but a vector of scaling functions in the MRA and, accordingly, matrix-valued scaling sequences.

The new JPEG2000 standard of image compression can use biorthogonal, 5/3 and 9/7 wavelets.

literature

Barbara Burke Hubbard: Wavelets: The Mathematics of Small Waves . 1st edition. Birkhäuser Verlag, 1997, ISBN 3-7643-5688-X .
Werner Bäni: Wavelets. An introduction for engineers . 2nd Edition. Oldenbourg Wissenschaftsverlag GmbH, 2005, ISBN 3-486-57706-9 .
Jöran Bergh, Frederik Ekstedt, Martin Lindberg: Wavelets with applications in signal and image processing . Springer Verlag, 2007, ISBN 978-3-540-49011-1 .
I. Daubechies: Where do wavelets come from? - A personal point of view . Article 74 in the list, published in: Proceedings of the IEEE, Special Issue on Wavelets 84 (no. 4), pp. 510-513, April 1996, doi: 10.1109 / 5.488696

Web links

Commons : Wavelet album with pictures, videos and audio files

A Really Friendly Guide to Wavelets by C. Valens
Wavelet Analysis in the Mathematica Wavelet Explorer documentation. Comprehensive description of the topic.

Individual evidence

↑ wavelet. Retrieved January 29, 2019 .

[1] wavelet. Retrieved January 29, 2019 .