De-sitter room

In mathematics and physics a -dimensional de-sitter space (after Willem de Sitter ) is noted , the Lorentz manifold analogous to an n - sphere (with its canonical Riemann manifold ); it is maximally symmetric , has a constant positive curvature and is simply connected for . ${\displaystyle n}$ ${\displaystyle dS_{n}}$ ${\displaystyle n\geq 3}$

In four-dimensional Minkowski space (3 space dimensions plus time) or in space-time , the de-sitter space is the analogue of a sphere in ordinary Euclidean space .

In the language of general relativity , the De Sitter space is the maximally symmetrical vacuum solution of Einstein's field equations with a positive (repulsive) cosmological constant (corresponding to a positive vacuum energy density and negative pressure) and thus a cosmological model for the physical universe ; see De-Sitter model . ${\displaystyle \Lambda }$

The De Sitter room was discovered in 1917 by Willem de Sitter and at the same time - independently of de Sitter - by Tullio Levi-Civita .

definition

2-dimensional de-sitter room. The radius and volume reach their minimum value at time t = 0.

The de-sitter space can be defined as the submanifold of a Minkowski space of a higher dimension .

So if you consider the Minkowski space with the usual metric tensor ${\displaystyle \mathbb {R} ^{1,n}}$

${\displaystyle ds^{2}=-dx_{0}^{2}+\sum _{i=1}^{n}dx_{i}^{2}.}$

Then the de-sitter space is the submanifold created by the single-shell hyperboloid

${\displaystyle \alpha ^{2}=-x_{0}^{2}+\sum _{i=1}^{n}x_{i}^{2},}$

is described, where is a positive constant with the dimension of a length. The metric tensor of the De Sitter space is the one that is generated by the metric tensor of the Minkowski space. One can check that the generated metric is not degenerate and has a signature of the form (1, k, 0). (If in the above definition is replaced by, a two-shell hyperboloid is obtained. In this case the generated metric is positive definite , and each of the two shells is a copy of a hyperbolic n- geometry .) ${\displaystyle \alpha }$ ${\displaystyle \alpha ^{2}}$ ${\displaystyle -\alpha ^{2}}$

The De-Sitter space can also be defined as the quotient of two Lorentz groups , which shows that it is a non- Riemannian symmetrical space . ${\displaystyle {\tfrac {\mathrm {O} (1,n)}{\mathrm {O} (1,n-1)}}}$

Topologically , the de-sitter space is of the form . ${\displaystyle \mathbb {R} \times S^{n-1}}$

properties

The isometric group of the De Sitter space is the Lorentz group . Hence the metric has independent killing vectors and is maximally symmetric. Every maximally symmetrical space has constant curvature. The Riemann curvature tensor of the De-Sitter space is ${\displaystyle \mathrm {O} (1,n)}$ ${\displaystyle {\tfrac {n(n+1)}{2}}}$ ${\displaystyle R_{\rho \sigma \mu \nu }}$

${\displaystyle R_{\rho \sigma \mu \nu }={1 \over \alpha ^{2}}(g_{\rho \mu }g_{\sigma \nu }-g_{\rho \nu }g_{\sigma \mu }).}$

The De Sitter space is an Einstein manifold since the Ricci tensor is proportional to the metric : ${\displaystyle R_{\mu \nu }}$ ${\displaystyle g_{\mu \nu }}$

${\displaystyle R_{\mu \nu }={\frac {n-1}{\alpha ^{2}}}\cdot g_{\mu \nu }.}$

That is, the De-Sitter space is a vacuum solution of Einstein's field equations with a cosmological constant

${\displaystyle \Lambda ={\frac {n-1}{\alpha ^{2}}}\cdot {\frac {n-2}{2}}.}$

The curvature scalar of this space is

${\displaystyle R={\frac {n(n-1)}{\alpha ^{2}}}={\frac {2n}{n-2}}\Lambda .}$

For n = 4 we get Λ = 3 / α ² and R = 4Λ = 12 / α ² .

Static coordinates

Static coordinates (time , radius , ...) can be introduced for the de-sitter space as follows : ${\displaystyle t}$ ${\displaystyle r}$

${\displaystyle x_{0}={\sqrt {\alpha ^{2}-r^{2}}}\cdot \sinh(t/\alpha )}$

${\displaystyle x_{1}={\sqrt {\alpha ^{2}-r^{2}}}\cdot \cosh(t/\alpha )}$

${\displaystyle x_{i}=rz_{i}}$ With ${\displaystyle 2\leq i\leq n,}$

where the standard embedding of the sphere in R represents ^{n −1} . ${\displaystyle z_{i}}$ ${\displaystyle S^{n-2}}$

In these coordinates the de-sitter metric takes the following form:

${\displaystyle ds^{2}=-\left(1-{\frac {r^{2}}{\alpha ^{2}}}\right)dt^{2}+\left(1-{\frac {r^{2}}{\alpha ^{2}}}\right)^{-1}dr^{2}+r^{2}d\Omega _{n-2}^{2}.}$

Note: there is a cosmological horizon at . ${\displaystyle r=\alpha }$

Slicing coordinates

Flat

Approach:

${\displaystyle x_{0}=\alpha \sinh(t/\alpha )+r^{2}e^{t/\alpha }/2\alpha }$

${\displaystyle x_{1}=\alpha \cosh(t/\alpha )-r^{2}e^{t/\alpha }/2\alpha }$

${\displaystyle x_{i}=e^{t/\alpha }y_{i}}$ With ${\displaystyle 2\leq i\leq n,}$

in which ${\displaystyle r^{2}=\sum _{i}y_{i}^{2}.}$

Then the metric of the de-sitter space in coordinates is: ${\displaystyle (t,y_{i})}$

${\displaystyle ds^{2}=-dt^{2}+e^{2t/\alpha }\cdot dy^{2}}$

with the flat metric up . ${\displaystyle dy^{2}=\sum _{i}dy_{i}^{2}}$ ${\displaystyle y_{i}}$

Closed

Approach:

${\displaystyle x_{0}=\alpha \sinh(t/\alpha )}$

${\displaystyle x_{i}=\alpha \cosh(t/\alpha )\cdot z_{i}}$ With ${\displaystyle 1\leq i\leq n,}$

where one describes a sphere. ${\displaystyle z_{i}}$ ${\displaystyle S^{n-1}}$

Then the metric of the de-sitter space is:

${\displaystyle ds^{2}=-dt^{2}+\alpha ^{2}\cosh ^{2}(t/\alpha )\cdot d\Omega _{n-1}^{2}.}$

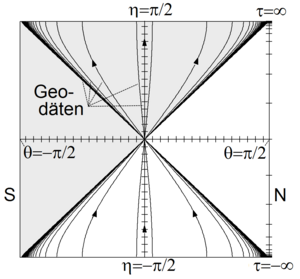
Penrose diagram of the De Sitter room. The η-coordinate compactizes the time τ to the interval [-π / 2, π / 2]. The angle θ describes in the interval [-π / 2, π / 2] any semicircle between any two antipodes S and N (the second semicircle is not shown). Light moves diagonally across the diagram to the top left or right. An observer at the North Pole (N) receives no signal from the upper left half (shown in gray).

If the time variable is changed to the conforming time : ${\displaystyle t}$ ${\displaystyle \eta }$

${\displaystyle {\begin{aligned}\tanh(t/\alpha )&=\tan(\eta )\\\Leftrightarrow \cosh(t/\alpha )&=1/\cos(\eta ),\end{aligned}}}$

this gives a metric that is conformally equivalent to the static Einstein universe :

${\displaystyle ds^{2}={\frac {\alpha ^{2}}{\cos ^{2}\eta }}(-d\eta ^{2}+d\Omega _{n-1}^{2}).}$

The De Sitter space and the Einstein universe therefore have the same Penrose diagram .

Open

Approach:

${\displaystyle x_{0}=\alpha \sinh(t/\alpha )\cosh \xi }$

${\displaystyle x_{1}=\alpha \cosh(t/\alpha )}$

${\displaystyle x_{i}=\alpha \sinh(t/\alpha )\sinh \xi \cdot z_{i}}$ With ${\displaystyle 2\leq i\leq n,}$

whereby a sphere forms with the standard metric ${\displaystyle \sum _{i}z_{i}^{2}=1}$ ${\displaystyle S^{n-2}}$ ${\displaystyle \sum _{i}dz_{i}^{2}=d\Omega _{n-2}^{2}.}$

Then the metric of the de-sitter space is

${\displaystyle ds^{2}=-dt^{2}+\alpha ^{2}\sinh ^{2}(t/\alpha )\cdot dH_{n-1}^{2},}$

with the metric of a hyperbolic Euclidean space. ${\displaystyle dH_{n-1}^{2}=d\xi ^{2}+\sinh ^{2}\xi \cdot d\Omega _{n-2}^{2}}$

DS

Approach:

${\displaystyle x_{0}=\alpha \sinh(t/\alpha )\cosh \xi \sin(\chi /\alpha )}$

${\displaystyle x_{1}=\alpha \cos(\chi /\alpha )}$

${\displaystyle x_{2}=\alpha \cosh(t/\alpha )\sin(\chi /\alpha )}$

${\displaystyle x_{i}=\alpha \sinh(t/\alpha )\sinh \xi \sin(\chi /\alpha )z_{i}}$ With ${\displaystyle 3\leq i\leq n}$

where one describes a sphere. ${\displaystyle z_{i}}$ ${\displaystyle S^{n-3}}$

Then the metric of the de-sitter space is:

${\displaystyle ds^{2}=d\chi ^{2}+\sin ^{2}(\chi /\alpha )\cdot ds_{dS,\alpha ,n-1}^{2},}$

in which

${\displaystyle ds_{dS,\alpha ,n-1}^{2}=-dt^{2}+\alpha ^{2}\sinh ^{2}(t/\alpha )\cdot dH_{n-2}^{2}}$

is the metric of a -dimensional de-sitter space in open slicing coordinates, with radius of curvature . ${\displaystyle n-1}$ ${\displaystyle \alpha }$

The hyperbolic metric is:

${\displaystyle dH_{n-2}^{2}=d\xi ^{2}+\sinh ^{2}\xi \cdot d\Omega _{n-3}^{2}.}$

This is the analytical continuation of the open slicing coordinates

${\displaystyle (t,\xi ,\theta ,\phi _{1},\phi _{2},\cdots ,\phi _{n-3})\to (i\chi ,\xi ,it,\theta ,\phi _{1},\cdots ,\phi _{n-4})}$

and also the exchange of and , because they change their time or space-like properties. ${\displaystyle x_{0}}$ ${\displaystyle x_{2}}$

Others

In the context of theories of quantum gravity, some authors suggested the de-sitter space instead of the Minkowski space as the fundamental space for special relativity and called this de-sitter relativity .

See also

• De-Sitter model
• Anti-de-sitter room
• Einstein de Sitter model

literature

• W. de Sitter: On the relativity of inertia: Remarks concerning Einstein's latest hypothesis . In: Proc. Con. Ned. Acad. Wet. tape 19 , 1917, pp. 1217-1225 .
• W. de Sitter: On the curvature of space . In: Proc. Con. Ned. Acad. Wet. tape 20 , 1917, pp. 229-243 .
• Tullio Levi-Civita : Realtà fisica di alcuni spazî normali del Bianchi . In: Rendiconti, Reale Accademia Dei Lincei . tape 26 , 1917, pp. 519-31 .
• K. Nomizu: The Lorentz-Poincaré metric on the upper half-space and its extension . In: Hokkaido Mathematical Journal . tape 11 , no. 3 , 1982, pp. 253-261 .
• HSM Coxeter : A geometrical background for de Sitter's world . In: Mathematical Association of America (Ed.): American Mathematical Monthly . tape 50 , no. 4 , 1943, pp. 217-228 , doi : 10.2307 / 2303924 , JSTOR : 2303924 .
• L. Susskind , J. Lindesay: An Introduction to Black Holes, Information and the String Theory Revolution: The Holographic Universe . 2005, p. 119 (5/11/25) .
• Qingming Cheng: De Sitter space . Jumper.

proof

1. ^ R. Aldrovandi, JG Pereira, de Sitter Relativity: a New Road to Quantum Gravity ?, arxiv.org, 2007