Dynamic system (system theory)

A dynamic system is a delimited, time-dependent functional unit that interacts with the environment through its signal inputs and signal outputs . The system can, for example, be a mechanical structure, an electrical network , but also a biological process or a component of the national economy .

The system has at least one signal input and one signal output and reacts at a specific point in time to any input signal with a specific time response to the output signal. The energy stores contained in the system as the cause of the time behavior can intentionally or unintentionally adopt a system state ≠ 0 in the state space, in which the effect of the input signal with the system behavior and the system state on the system output signal is superimposed.

Elementary terms of the dynamic system

A technical dynamic system contains one or more energy stores that are arranged in a concentrated or spatially distributed manner. In system calculations, concentrated energy stores are often assumed to simplify matters. Dynamic systems with concentrated system memories contain variables as a function of time. Dynamic systems with spatial distribution of system memories contain variables as functions of time and place.

A dynamic system is a functional unit for processing and transmitting signals, whereby the system input variable is defined as the cause and the system output variable as the temporal effect.

Furthermore, the internal energy stores can contain initial values if the signal behavior of a system at a specific point in time within a transient process is to be considered. ${\displaystyle t_{0}\,}$ ${\displaystyle t>0\,}$

• The output-input behavior of these systems can be linear , continuously non-linear , discontinuous non-linear, time-invariant , time-variant and subject to dead time . This applies to single-size and multi-size systems.

• Definition of linearity: A system behaves linearly if it fulfills the superposition principle (superposition principle) and the reinforcement principle.

A graphical representation of the output input behavior of the linear dynamic system with asymptotically stable behavior must always show an unlimited straight line after a sufficiently long time, which can be offset from the origin.

System separation into static non-linear system and linear dynamic system.

• Definition of non-linear system: Static continuously non-linear systems change their gain according to a certain function. Nonlinear dynamic systems cause problems in system calculation because they can rarely be solved analytically. Usual system descriptions are carried out by numerical, discrete-time calculation with logical commands and difference equations. For easier calculation, non-linear dynamic systems can also be divided by models in combinations of non-linear systems without time behavior and linear dynamic systems, e.g. B. after the Hammerstein model . Nonlinear static models are mostly unique.

• Complex dynamic systems generally consist of several sub-systems of a certain structure, which are shown in signal flow diagrams (block diagrams) as series, parallel and feedback circuits.

• Static linear or non-linear systems have no energy storage and therefore no time behavior. The output-input behavior is described by algebraic or transcendent functions or value tables.

• → See Wikibooks: Introduction to Systems Theory / Description of Linear Processes in the Time Domain :

Wikibooks: Linearity Properties  - Learning and Teaching Materials

Mathematical procedures for system description and system calculation

Mathematical models of dynamic systems are characterized or approximated by various mathematical description methods depending on the knowledge and availability of the system parameters.

The best known system description is the differential equation . Other known system descriptions of dynamic systems can be developed from the differential equations, such as the transfer function with the complex frequency range F (s), the frequency response F (jω), the state space representation f (t), the difference equations f (k, required for the numerical calculation) Δt), as well as the associated z-transfer function .

The calculation of dynamic systems serves the knowledge of the output input behavior and the system analysis . Depending on the type of dynamic system, different mathematical description and calculation methods are suitable.

Dynamic systems with dead time behavior (transport time) can practically only be calculated with numerical time-discrete methods.

Overview of differential equations

• Ordinary higher order differential equation with constant coefficients

A common differential equation is an equation that contains one or more derivatives of an unknown function. The term "common" refers to the fact that the function you are looking for only depends on one variable. A linear ordinary differential equation contains the function and its derivatives only in the first power. The function you are looking for must not appear in the arguments of trigonometric functions, logarithms, etc., otherwise the differential equation becomes non-linear. Nonlinear differential equations with the various types of nonlinearity can only be solved analytically in very rare exceptional cases. Such dynamic systems can be described and calculated using numerical discrete-time methods.

The most common mathematical system descriptions of linear systems are ordinary differential equations with constant coefficients. To set up the higher order differential equations, balance equations of the energy / matter stores are required. Systems with concentrated storage require a first-order differential equation for each storage function.

With dynamic systems in the form of executed technical systems, differential equations are rarely available. The system behavior must first be analyzed and then formulated.

Example of an ordinary differential equation of the nth order with constant coefficients a and b for a system with the output signal y (t) and input signal u (t):

${\displaystyle a_{n}y^{(n)}+\ldots +a_{2}{\ddot {y}}+a_{1}{\dot {y}}+a_{0}y=b_{m}u^{(m)}+\ldots +b_{2}{\ddot {u}}+b_{1}{\dot {u}}+b_{0}u\,}$

Conventional solution of the ordinary differential equation:

A differential equation (DGL) is always solved by integration and is a function, not a value.

The approach (λ = zero) results in a universal solution method for the homogeneous solution of the differential equation of any order with constant coefficients (see characteristic equation ). ${\displaystyle y=e^{{\lambda }\cdot t}\,}$

• Complete solution consists of two parts of the solution: y (t) = homogeneous solution y _H (t) + particulate solution y _P (t)

• Homogeneous solution: ${\displaystyle y_{H}(t)=C_{1}\cdot e^{{\lambda }_{1}\cdot t}+C_{2}\cdot e^{{\lambda }_{2}\cdot t}+C_{3}\cdot e^{{\lambda }_{3}\cdot t}+\cdots }$

Condition: The homogeneous solution only refers to initial values. The system input excitation is zero. Disadvantage: laborious calculation of the integration constant C.

• Particulate solution for the DGL using the convolution integral or the Laplace transformation . ${\displaystyle y_{p}(t)\,}$

Condition: All initial values ​​are zero. The input excitation is non-zero. The convolution integral for higher order systems is difficult to solve.

Solution of the temporal system behavior from the transfer function of the DGL for a given input signal U (s):

With the usual higher-order differential equation, the solution using the Laplace transformation or the numerical calculation with discrete time is more suitable. When used to solve a differential equation using the transfer function using the inverse Laplace transformation, the analytical solution in the time domain is found using the search term in the Laplace transformation table in operator notation.

${\displaystyle y(t)={\mathcal {L}}^{-1}\underbrace {\left\{G(s)\cdot U(s)\right\}} _{\text{Suchbegriff}}}$

• Higher order differential equation with variable coefficients

  • If these coefficients or only one coefficient of this differential equation are variable, then the time behavior of the dynamic system changes, i.e. H. a step response of the system for a given input step takes a different time course. This behavior is easy to understand if one considers the Laplace transformed differential equation as a transfer function.
  • If the coefficients are time-dependent, this leads to time-variant system behavior, i.e. H. the time behavior of the system is different at different times for t> t ₀ . System example: When the mass of the propellant changes in an accelerated rocket.

• Partial differential equation

In the case of partial differential equations , the function you are looking for depends on several variables. It is derived from several variables. The application of this equation takes place e.g. B. in dynamic systems with time and location coordinates.

System example: Signal transmission with long electrical lines or heat flow in homogeneous media (liquids, metals, stone).

Basics of the Laplace transfer function

Block diagram of a transfer function as a single and multiple variable system.

The transfer function with the complex frequency s results from the Laplace transform of a linear differential equation with constant coefficients. The resulting polynomial equation is broken down into linear factors by determining the pole zeros (s _p and s _n ). The forms of representation of the transfer function as a rationally broken function differentiate between the factored pole-zero representation and the time constant representation. ${\displaystyle G(s)=Y(s)/U(s)}$

${\displaystyle \underbrace {(s-s_{p})} _{\text{Produktterm}}=\underbrace {s_{p}\cdot \left({\frac {1}{s_{p}}}\cdot s+1\right)} _{s_{p}={\text{negativer Wert}}}=\underbrace {k\cdot (T\cdot s+1)} _{\text{Zeitkonstantendarstellung}}}$

Other forms of development are possible using system identification methods using test signals, by measuring the frequency response of the system or using voltage dividers from a non-reactive impedance ratio. ${\displaystyle G(j\omega )}$

The transfer function is the most common system representation because there are only 3 forms - each in the numerator and denominator - of linear factors or their multiples of differentiating and delaying linear elementary basic systems and the recognition of the system based on the equation is high.

All terms in the numerator and denominator of the transfer function can be treated algebraically. In the time domain, linear factors in the denominator determine the system time behavior and have an integrating or time-delaying effect. Linear factors in the numerator determine the size of the amplitudes and have differentiating behavior.

The transfer function in polynomial representation and time constant representation with T = 1 / s _p and Tv = 1 / s _n is:

${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0}}}=K\cdot {\frac {(T_{V1}\cdot s+1)(T_{V2}\cdot s+1)\dotsm (T_{Vm}\cdot s+1)}{(T_{1}\cdot s+1)(T_{2}\cdot s+1)\dotsm (T_{n}\cdot s+1)}}}$

State space model of a 1st order transmission system.

Explanation of terms state space representation

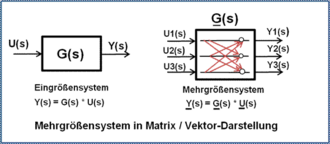
The term state space representation is the description of a dynamic transmission system through its state variables (= state variables). The system-describing differential equation of the nth order with n concentrated energy stores is broken down into n differential equations of the 1st order and brought into a matrix / vector representation. The status variables physically describe the energy content of the storage elements contained in a technical dynamic system.

Linear and non-linear dynamic systems, including multi-variable systems, can be treated in this way. Linear dynamic systems with initial values ​​can be calculated numerically relatively easily with the normal control form of the state space, without transferring to the matrix / vector representation.

Basics "Numerical Calculation of Dynamic Systems"

Rectangular approximation of a PT1 element by calculation with a difference equation.

For the calculation of linear and non-linear systems with dead time, only the numerical calculation with the discrete time Δt can be used. In its simplest form it corresponds to the human way of thinking for a linear system in the operator representation of the output signal for a given input signal . ${\displaystyle y_{(k\cdot t)}}$ ${\displaystyle u_{(k\cdot t)}}$

${\displaystyle y_{(k\cdot t)}=f({\text{System}},k,\Delta t,u_{(k\cdot t)})}$

Depending on the system properties, a new output signal is calculated step by step for a small time difference . For each new calculation sequence of a subsystem, the current output signal relates additively to a previous sequence . ${\displaystyle y_{(k)}}$ ${\displaystyle k=(0;1;2;3\cdots k_{i})}$ ${\displaystyle y_{(k)}}$ ${\displaystyle y_{(k-1)}}$

Numerical solutions for the calculation of the system behavior are usually presented in a table in k _i lines. Each line contains the same logic commands (for non-linearity) and difference equations.

Difference equation

In the simplest case, difference equations describe differential equations of the first order, the differential quotients of which have been exchanged for difference quotients . All linear systems of higher order can be described with the help of 4 types of difference equations, including oscillating systems with conjugate complex pole pairs. ${\displaystyle \Delta y/\Delta t}$

Example of the integration function in operator representation:

${\displaystyle y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T}}}$

Sampled linear dynamic systems in online operation as well as simulations of dynamic systems are calculated using difference equations.

Calculation examples of linear systems

Separately excited DC shunt motor with asymptotic behavior

It is a linear asymptotically stable system with a system input u (t) as armature voltage and a system output y (t) as speed. This system is described by a common second order differential equation (time delays: inductance of the magnet coils, magnetic force to accelerate the armature mass).

Step responses from 4 series-connected PT1 elements, each with the same time constant T = 1 [s].

After a sufficiently long time, the rest position of the system is proportionally dependent on the size of the input signal.

It is a 2nd order delay system that has 2 real poles in the complex frequency range.

System-describing ordinary differential equation with the coefficients a _n and b _m :

${\displaystyle a_{2}\cdot {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)\,}$

Using the Laplace transformation of the differential equation results in the polynomial representation of the transfer function G (s). With the help of the pole-zero decomposition, the product representation of the transfer function results.

Transfer function in time constant representation:

${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {K}{(T_{1}\cdot s+1)(T_{2}\cdot s+1)}}}$

Solution of the function of the system output variable with the help of the Laplace transformation tables for a normalized input step 1 (t): ${\displaystyle {\mathcal {L}}^{-1}\,\{1(t)\}=1/s}$

${\displaystyle y(t)=K\cdot [1+{\frac {1}{T_{2}-T_{1}}}({T_{1}\cdot e^{-{\frac {t}{T_{1}}}}}-{T_{2}\cdot e^{-{\frac {t}{T_{2}}}}})]}$

Numerical calculation of a 2nd order transmission system with the help of the normal control form of the state space representation

The solution of a system-describing differential equation by an analog computer, which was preferred until the 1960s, is very similar to the normal control form of the state space .

The output values ​​of the integrators can have the value zero at any selectable point in time , or they can be set to any initial value , regardless of whether the input variable has a value not equal to zero or equal to zero. The outputs of the integrators are the state variables and the solutions of the differentials, in that they are fed back to the input of the highest derivative with the associated coefficients. The function of the output variable you are looking for corresponds to the status variable . ${\displaystyle t_{0}}$ ${\displaystyle y_{0},y'_{0},y''_{0}\cdots }$ ${\displaystyle u(t)}$ ${\displaystyle x_{n}(t){\text{ bis }}x_{1}(t)}$ ${\displaystyle y(t)}$ ${\displaystyle x_{1}(t)}$

The calculation of the signal flow diagram is carried out numerically and refers to the explicit form of the differential equation, in which the highest derivative of the output variable is exempt from the equation. ${\displaystyle y^{n}(t)}$

Example of the GDGL of a spring-mass damping system with the input signal ${\displaystyle u(t)}$

In the university department of technical fields of study, the spring pendulum is defined as a second-order transmission system in many cases as a system with an entrance and an exit. The linearly damped oscillating system usually has a system input and a system output as the position (location) of the mass. The following use cases occur: ${\displaystyle u(t)}$ ${\displaystyle y(t)}$

• Use case ${\displaystyle u(t)>0}$

The input variable attacks the body of the mass with a force and moves the body as output variable . The movement is opposed by the inertia, damping and restoring force of the spring. ${\displaystyle u(t)}$ ${\displaystyle F}$ ${\displaystyle m}$ ${\displaystyle y(t)}$

After a sufficiently long time, the rest position of the mass is dependent on the input variable , the spring constant and the mass . ${\displaystyle u(t)}$ ${\displaystyle f}$ ${\displaystyle m}$

• Use case ${\displaystyle u(t)=0}$

The system with is in motion when initial values and their derivatives of the internal energy storage are given at the time. ${\displaystyle y(t)}$ ${\displaystyle t=0}$ ${\displaystyle y_{0}}$

After a long enough time, the rest position of the mass is determined by the size of the mass and the spring force.

The spring pendulum is a linear 2nd order delay system which has a complex conjugate pole pair in the complex frequency range. The system vibrates dampened if the size of the degree of damping is in the range . ${\displaystyle d}$ ${\displaystyle 0<d<1}$

Differential equation of the oscillating movement with signal input and signal output : (m = mass, d = damping constant, k = spring constant, b ₀ = factor) ${\displaystyle u(t)}$ ${\displaystyle y(t)}$

${\displaystyle m\cdot {\ddot {y}}(t)+d\cdot {\dot {y}}(t)+k\cdot y(t)=b_{0}\cdot u(t)}$

Signal flow diagram for the homogeneous and particulate solution of the second order GDGL

Signal flow diagram of the normal control form for a 2nd order system without differentials of the input signal u (t) to determine the state variables x1 (t), x2 (t).

In the signal flow diagram shown, all the coefficients of the GDGL have been divided by the coefficient of the highest derivative in order to be able to release them. The signal flow diagram corresponds to the explicit representation of the GDGL, i.e. the form of the exempted equation according to the highest derivative . ${\displaystyle a_{2}}$ ${\displaystyle {\ddot {y}}(t)}$ ${\displaystyle {\ddot {y}}(t)}$ ${\displaystyle y^{(n)}=f(t;\ y;\ {\dot {y}};\ {\ddot {y}}\ \cdots )}$

The signal flow diagram is calculated numerically as shown by performing each mathematical operation of the coefficients and difference equations in sequence. Since the result of the numerical calculation is always in the form of a table, all calculations belong in one line according to the sequence . Each equation occupies a column of the same row. It will be calculated identical lines in a row. ${\displaystyle k}$ ${\displaystyle k_{\mathrm {max} }}$

The general form of the oscillation equation is:

${\displaystyle a_{2}\cdot {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)}$

To carry out the calculation, the GDGL is converted and released according to the highest derivation . ${\displaystyle y^{(n)}(t)}$

${\displaystyle {\ddot {y}}(t)={\frac {b_{0}}{a_{2}}}\cdot u(t)-{\frac {a_{1}}{a_{2}}}\cdot {\dot {y}}(t)-{\frac {a_{0}}{a_{2}}}\cdot y(t)}$

The signal flow diagram shown forces the solution of the second order GDGL for . It now depends on whether one: ${\displaystyle y(t)}$

• homogeneous solution with initial values ​​and , ${\displaystyle u(t)=0}$
• particulate solution with no initial values, ${\displaystyle u(t)\neq 0}$
• an overall solution with initial values ​​and is desired. ${\displaystyle u(t)\neq 0}$

The following numerical operations are required to calculate the components of the signal flow plan:

Algebraic operations such as B. the difference of the coefficients from the input variable are numbered according to the sequence or the subsequent equations. ${\displaystyle u(t)}$ ${\displaystyle k}$

${\displaystyle {\frac {u_{(k)}\cdot b_{0}}{a_{2}}}-{\frac {a_{1}}{a_{2}}}-{\frac {a_{0}}{a_{2}}}}$.

The input variable is for the homogeneous solution . ${\displaystyle u_{(k)}=0}$

The difference equation of integration (Euler backward) applies to the calculation of the integrators:

${\displaystyle y_{k}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}}$

The term here generally means the input quantity for each sequence of the difference equation. In most cases this is not the system input variable , but rather the input value shown in the table, which is in the same line to the left of the column of the difference equation. Depending on the task, it changes constantly with increasing sequence. If there are several difference equations connected in series, the output variable is the input variable for the next difference equation . ${\displaystyle u_{(k)}}$ ${\displaystyle u(t)}$ ${\displaystyle u_{(k)}}$ ${\displaystyle y_{(k)}}$ ${\displaystyle u_{(k)}}$

The integration constant has the value 1 without any special specification. ${\displaystyle T_{I}}$

${\displaystyle y_{(k-1)}}$refers to the result of a sequence (row) in the past in the same column of the difference equation. ${\displaystyle k-1}$

Since there are two integrators connected in series, the output variable of the first integrator is the input variable of the second integrator. The output variable of the second integrator is the function of the same sequence that is sought for a support point that approximates the analytical function. ${\displaystyle y_{(k)}}$

If the initial values ​​of the GDGL are available, the initial values ​​of the two difference equations are entered for the corresponding integrator for the calculation sequence instead of the value (1st line of the table) . ${\displaystyle k=0}$ ${\displaystyle y_{(k)}=0}$ ${\displaystyle y_{(k=0)}=y_{0}^{'}\ {\text{bzw.}}\ =y_{0}}$

Since the numerical solution of the GDGL represents an approximation of the original function, the accuracy of the calculation for the specified difference equation depends on the size of the discrete time. If a value of approx. 0.1% of the dominant system time constant is selected, an approximation error of approx. 0.1% is to be expected. ${\displaystyle \Delta t}$

Example of the homogeneous solution of a vertically oscillating spring pendulum without an input signal with initial values ${\displaystyle u(t)=0}$

Time behavior of the position of the mass of the spring pendulum without signal input. Oscillation period: 2.54 [sec], damping D = 0.15. Example numerical values: m = 0.16; d = 0.12; k = 1; y ₀ = 1

See picture: Signal flow diagram of the normal control form for a 2nd order transmission system!

The spring pendulum can also be defined as a system with an input signal = zero at the point in time with the initial values ​​of the spring force and the mass. In this case, the system is left to its own devices at the moment and strives for a rest position that is determined by the spring force, mass and damping. ${\displaystyle t_{0}}$ ${\displaystyle t_{0}}$

The initial values ​​are defined as follows:

• The position of the mass at rest is defined as zero.
• The position of the mass is defined raised to a level with the initial value and dropped at the point in time . ${\displaystyle y_{0}=1}$ ${\displaystyle t=0}$
• The initial value of the first integrator must have the value zero when the mass is raised , otherwise the initial value cannot remain at the initial value . A constant output value with two integrators connected in series is only possible if the output value of the first integrator is zero. ${\displaystyle y'_{0}}$ ${\displaystyle y'_{0}=0}$ ${\displaystyle y_{0}=1}$ ${\displaystyle y_{0}=1}$

The following recursive calculations according to the signal flow plan are required for the homogeneous solution of the GDGL of the spring pendulum:

• The input variable is zero. ${\displaystyle {\frac {u_{(k)}\cdot b_{0}}{a_{2}}}}$

${\displaystyle -{\frac {a_{1}}{a_{2}}}\cdot y'_{(k)}-{\frac {a_{0}}{a_{2}}}\cdot y_{(k)}}$. These output variables of the integrators evaluated with the coefficients act as input variables . ${\displaystyle {\ddot {y}}(t)}$

• Difference equation of the first I term:

${\displaystyle y_{k}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}}$. The output value of the first integrator is the input value of the second integrator. ( ) ${\displaystyle T_{I}=1}$

• Difference equation of the second I-term:

${\displaystyle y_{k}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}}$. The output value of the second integrator is the result of a calculation line. ( ) ${\displaystyle y_{k}}$ ${\displaystyle T_{I}=1}$

• The first calculation line for contains the initial values ​​of the integrators and the difference equations. All other equations on this line have the value zero. ${\displaystyle y_{(k=0)}}$ ${\displaystyle {\dot {y}}_{0}(t)=0}$ ${\displaystyle y_{0}(t)=1}$

If these equations are also calculated for a graphical representation with a viewing time of 10 seconds , 1000 identical calculation sequences (lines) are required. Each episode provides a distance for a value. The largest approximation error is about 1% due to the selected size . ${\displaystyle \Delta t=0{,}01\,\mathrm {s} }$ ${\displaystyle \Delta t}$ ${\displaystyle y_{(k)}}$ ${\displaystyle \Delta t=0{,}01\,\mathrm {s} }$

With the exception of the subsequent equation for (1st line), all other subsequent equations (lines) are identical. ${\displaystyle k=0}$

Tabular calculation of the pendulum:

The values ​​of and are not yet available for calculating the coefficients as the input variable of the first integrator of the sequence . Therefore these values ​​have to be taken from a previous sequence . To avoid rounding errors that add up, the calculation was made with a very high number of digits in the spreadsheet. ${\displaystyle k}$ ${\displaystyle y'_{(k)}}$ ${\displaystyle y_{(k)}}$ ${\displaystyle k-1}$

Episode k	Discrete time ${\displaystyle t_{(k)}}$	Coefficients ${\displaystyle -0{,}75\cdot y'_{(k)}-6{,}25\cdot y_{(k)}}$	First numerical integration ${\displaystyle y'_{(k)}}$	Second numerical integration ${\displaystyle y_{(k)}}$
0	0	0	${\displaystyle y'_{0}=0}$	${\displaystyle y_{0}=1}$
1	0.01	−6.250	−0.0625	0.999375
2	0.02	−6.199219	−0.1244922	0.998130
3	0.03	−6.144944	−0.1859416	0.9962706
126	1.26	3,929768	−0.0337729	−0.6203322

See numerical values ​​in the last picture for and . ${\displaystyle t_{(k=126)}=1{,}26\ [sec]}$ ${\displaystyle y_{(k=126)}=-0{,}62}$

Particulate solution of the GDGL of a vertically oscillating spring pendulum with an input signal without initial values ${\displaystyle u(t)>0}$

The following recursive calculations according to the signal flow plan are required for the particular solution of the GDGL of the spring pendulum:

• The input variable is selected for a standardized jump . ${\displaystyle {\frac {u_{(k)}\cdot b_{0}}{a_{2}}}}$ ${\displaystyle u(t)=1}$

${\displaystyle {\frac {b_{0}}{a_{2}}}\cdot u_{(k)}-{\frac {a_{1}}{a_{2}}}\cdot y'_{(k)}-{\frac {a_{0}}{a_{2}}}\cdot y_{(k)}}$. These evaluated coefficients act as an input variable ${\displaystyle {\ddot {y}}(t)}$

• Difference equation of the first I term:

${\displaystyle y_{k}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}}$. The output value of the first integrator is the input value of the second integrator. ( ) ${\displaystyle T_{I}=1}$

• Difference equation of the second I-term:

${\displaystyle y_{k}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}}$. The output value of the second integrator is the result of a calculation line. ( ) ${\displaystyle y_{k}}$ ${\displaystyle T_{I}=1}$

• The first calculation line for contains the initial values ​​of the integrators and the difference equations. All other equations on this line have the value zero. ${\displaystyle y_{(k=0)}}$ ${\displaystyle {\dot {y}}_{0}(t)=0}$ ${\displaystyle y_{0}(t)=0}$

The result of the numerical calculation is a mirror-image representation of the course of the homogeneous solution for the selected data. The system starts oscillating at damped and asymptotically approaches the value 1 after a sufficiently long time. ${\displaystyle y(t)}$ ${\displaystyle y_{(k)}}$ ${\displaystyle \Delta t=0}$

The overall solution of the GDGL for the selected data is for all consequences . ${\displaystyle y_{H}(t)+y_{P}(t)}$ ${\displaystyle y_{(k)}=1}$

See also

• 

  Portal: Measurement, control and regulation technology  - overview of Wikipedia content on the subject of measurement, control and regulation technology
• Difference equation
• State space representation
• System identification

Wikibooks: Introduction to Systems Theory  - Learning and Teaching Materials

literature

• Bernd Girod, Rudolf Rabenstein, Alexander Stenger: Introduction to system theory, signals and systems in electrical engineering and information technology . 4th edition. Teubner-Verlag, 2007, ISBN 978-3-8351-0176-0 .
• Jan Lunze: Control engineering 1: System theory basics, analysis and design of single-loop controls . 7th edition. Springer, 2008, ISBN 3-540-68907-9 .
• Holger Lutz, Wolfgang Wendt: Pocket book of control engineering with MATLAB and Simulink . 11th edition. Europa-Lehrmittel, 2019, ISBN 978-3-8085-5869-0 .
• Rolf Unbehauen, Systems Theory Vol. 1 , 8th corr. Edition, Oldenbourg 2002, ISBN 3-486-25999-7
• Günter Ropohl , A system theory of technology - On the basis of general technology , Carl Hanser Verlag 1979, ISBN 3-446-12801-8

Individual evidence

1. ↑ Prof. Dr.-Ing. O. Sawodny, University of Stuttgart, “System-dynamic basics of control engineering”.
2. ↑ Prof. M. Ottens, University of Applied Sciences Berlin, lecture manuscript: "Fundamentals of Systems Theory".