Hermit interpolation

In numerical mathematics , Hermit interpolation (named after Charles Hermite ) is an interpolation method for polynomial interpolation that also takes derivatives of the function to be interpolated into account.

preparation

motivation

Spline interpolation without taking the slope into account. You can clearly see the "kink" at ${\displaystyle x=0{,}5}$

One result for the classic polynomial interpolation states that equidistant interpolation points - i.e. the same distance between the known function values ​​- leads to an exponential increase in the condition of the polynomial interpolation, and therefore increases its error drastically.

In practice, however, equidistant measuring points have certain advantages and are sometimes unavoidable. An interpolation method is therefore required that produces only small errors in this case too. One approach is spline interpolation , in which the area on which a function is to be interpolated is divided up by a grid and a polynomial interpolation is carried out in each of the resulting intervals.

Spline interpolation taking the slope into account

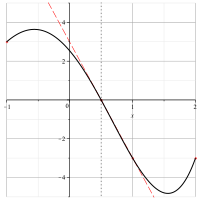
If the “naive” Newtonian approach is chosen, the derivatives of the interpolated at the grid points do not necessarily match - consequently, the interpolated at these points is usually not (continuously) differentiable . It does not have to stay with "corners", as in the example on the right. It could also happen, for example, that the interpolates approach the grid point “from above” on two adjacent intervals and thus actually a - vividly - “peak” arises.

Since this behavior is obviously undesirable, an attempt is made to make the transitions smooth by assuming any number of derivatives as known in addition to the function values ​​in the grid points and choosing the interpolation polynomials so that the derivatives coincide at the common point. In practice, it is sufficient to equate the first derivative in order to obtain a graph that looks "smooth".

This task can be solved analytically analogous to the problem in classic polynomial interpolation . The example here is the task

${\displaystyle f(-1)=-1,\,f'(-1)=0,\,f(2)=0}$in interpolate. ${\displaystyle {\mathcal {P}}_{2}}$

One defines

${\displaystyle p(x):=a_{0}+a_{1}\cdot x+a_{2}\cdot x^{2}}$and derives to . ${\displaystyle p'(x):=a_{1}+a_{2}\cdot 2x}$

The system of equations thus becomes

${\displaystyle {\begin{pmatrix}1&-1&1\\0&1&-2\\1&2&4\end{pmatrix}}\cdot {\begin{pmatrix}a_{0}\\a_{1}\\a_{2}\end{pmatrix}}={\begin{pmatrix}-1\\0\\0\end{pmatrix}}.}$

Solve for brings the coefficients we are looking for. ${\displaystyle a=(a_{0},a_{1},a_{2})^{T}}$

This approach has the disadvantage that it is in the complexity class and is therefore slow. It would be desirable to be able to adopt the Newton basis from the classic polynomial interpolation. However, this approach excludes coincident support points and can therefore not be used without modification. Therefore it is extended to Hermit's interpolation method. ${\displaystyle {\mathcal {O}}(n^{3})}$

Hermite Genocchi formula

The Hermite-Genocchi formula forms the basis of Hermite interpolation. The prerequisites of the sentence are:

• ${\displaystyle f}$is -time continuously differentiable : ${\displaystyle k}$ ${\displaystyle f\in C^{k}([a,b]),\quad k\in \mathbb {N} }$
• ${\displaystyle k+1}$ Support points: ${\displaystyle x_{0},\ldots ,x_{k}\in [a,b].}$

The formula now provides an integral representation for the divided differences from Newton's algorithm of polynomial interpolation:

${\displaystyle f[x_{0},\ldots ,x_{k}]=\int _{\Sigma ^{k}}f^{(k)}\left(x_{0}+\sum _{i=1}^{k}s_{i}(x_{i}-x_{0})\right)\,ds,}$

with the k-dimensional unit simplex :

${\displaystyle \;\Sigma ^{k}=\left\{s\in \mathbb {R} ^{k}{\bigg |}\,(\forall i:s_{i}\geq 0)\,\wedge \sum _{i=1}^{k}s_{i}\leq 1\right\}.}$

This identity is proven by complete induction.

In contrast to the divided differences, in the integral in this formula there is no quotient with the difference between two support points - purely arithmetically, it is therefore possible to use confluent (coincident) support points. If you put the formula as

${\displaystyle f[x_{0},\ldots ,x_{k}]={\frac {1}{k!}}f^{(k)}(x^{*}),\quad \mathrm {falls} \quad x_{0}=\ldots =x_{k}=x^{*}}$

this identity is easy to prove.

Obviously, one can take into account derivatives in the interpolation by using multiple support points.

So the following theorem applies:

Hermit interpolation

The following applies:

• ${\displaystyle f}$is -time continuously differentiable : ${\displaystyle n}$ ${\displaystyle f\in C^{n}([a,b]),\quad n\in \mathbb {N} }$
• ${\displaystyle n+1}$ Support points: ${\displaystyle x_{0},\ldots ,x_{n}\in [a,b]}$
• the frequency of the repetition of the support point is given. ${\displaystyle x_{i}}$ ${\displaystyle m_{i}\in \mathbb {N} }$

Then the Newton polynomial satisfies :

${\displaystyle p(x):=f(x_{0})+\sum _{i=1}^{n}f[x_{0},\ldots ,x_{i}]\prod _{j=0}^{i-1}(x-x_{j})}$

the Hermitian interpolation conditions :

${\displaystyle f^{(k)}(x_{i})=p^{(k)}(x_{i})\quad \forall \,i=0,\ldots ,n\ \forall k=0,\ldots ,m_{i}-1.}$

Furthermore, this solution is clear.

Error estimation

There is an explicit representation for the Hermit interpolated error . ${\displaystyle p}$

Be for it . Then for each one , so ${\displaystyle f\in C^{n+1}([a,b])}$
${\displaystyle x\in [a,b]}$ ${\displaystyle \xi \in [a,b]}$

${\displaystyle f(x)-p(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0}^{n}(x-x_{i})}$

applies.
In the case of the grid

${\displaystyle x_{0}=\ldots =x_{k}<x_{k+1}<\dots <x_{n}}$

applies:

${\displaystyle f(x)-p(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-x_{0})^{k+1}\prod _{i=k+1}^{n}(x-x_{i}).}$

Chebyshev abscissa

The second factor of the error formula only depends on the support points and can be estimated as follows.

Be arbitrary. Now the estimate applies: ${\displaystyle x_{0},\ldots ,x_{n}\in I:=[-1,1]}$

${\displaystyle \max _{x\in I}\prod _{i=0}^{n}|x-x_{i}|\geq 2^{-n}.}$

This limit is assumed by means of a special choice of support points - the so-called Chebyshev abscissas :

${\displaystyle {\begin{aligned}x_{j}&:=\cos \left({\frac {2j+1}{n+1}}{\frac {\pi }{2}}\right),\quad j=0,\ldots ,n\\\Rightarrow \max _{x\in I}\prod _{i=0}^{n}|x-x_{i}|&=2^{-n}.\end{aligned}}}$

Calculation of the interpolated

For the practical calculation of the interpolated, the scheme of the divided differences is used as before .

In this case , instead of the formula used there ${\displaystyle x_{0}=x_{1}=\ldots =x_{k}}$

${\displaystyle f[x_{0},\ldots ,x_{k}]={\frac {1}{k!}}f^{(k)}(x_{0})}$

be calculated.

It should be noted that some rearrangements are also necessary. In the following : ${\displaystyle x_{0}=\ldots =x_{i}=\ldots =x_{k}=\ldots =x_{n}}$

• Instead you have to the divided difference calculate ${\displaystyle f[x_{i},\ldots ,x_{k}]}$ ${\displaystyle f[x_{0},\ldots ,x_{k-i}]}$
• If it appears in the recursion , one calculates instead ${\displaystyle f[x_{i}]}$ ${\displaystyle f[x_{0}]}$
• In all cases where the formula from the original Neville-Aitken scheme is used, replace each with . ${\displaystyle x_{i}}$ ${\displaystyle x_{0}}$

Pseudocode

The purpose of the pseudocode is to illustrate how to compute the generalized form of the divided differences. In the following, lists are assumed to be indexed from 1 onwards.

xvals ← Stützstellen
yvals ← Funktionswerte f(x) und ggf. Ableitungen bei mehrfachen x-Werten
zvals ← { f(xvals[i]) | i ∈ 1..#xvals }

for i ← #xvals..1 do
  for j ← i..#xvals do
    if i = j then
      [xi..xj]f ← zvals[i]
    else if xvals[i] = xvals[j] then
      index ← Index des ersten Vorkommens von xvals[i] in xvals
      [xi..xj]f ← yvals[j - i + index] / (j-i)!
    else
      [xi..xj]f ← ([xi+1..xj]f - [xi..xj-1]f) / (xvals[j] - xvals[i])

history

Hermite first published his investigations on Hermit interpolation in 1878 in: Sur la formule d'interpolation de Lagrange . In: Journal for pure and applied mathematics , Volume 84, pp. 70–79.

Web links

Wikibooks: Hermit interpolation  - implementations in the algorithm collection

literature

• Richard L. Burden, J. Douglas Faires: Numerical Methods . Spectrum, Akad. Verlag, Heidelberg / Berlin / Oxford 2000, ISBN 3-8274-0596-3 .

Individual evidence

1. ↑ AH Turetskii: The bounding of polynomials prescribed at Equally distributed points. In: Proc. Pedag. Inst. Vitebsk; 3, 1940.
   See also Runge's phenomenon
2. ↑ Ralf Kornhuber, Christof Schütte: Introduction to Numerical Mathematics . Ed .: AG Numerical Mathematics. Free University of Berlin April 2008, 3.1.1 Hermite interpolation and Taylor's formula, p. 39–45 ( PDF, 2.4 MB - lecture notes).
3. ↑ Wolfgang Dahmen, Arnold Reusken: Numerics for engineers and natural scientists . Springer-Verlag, 2006, p. 281 .
4. ↑ Elliot Ward Cheney: Introduction to Approximation Theory . McGraw-Hill Book Company, 1966, ISBN 0-07-010757-2 , pp. 225, 242