
Example of a spline with 8 nodes
When spline interpolation given one tries to support points , also called node to using piecewise polynomials low grade interpolate . While the result of a polynomial interpolation often oscillates beyond recognition due to disadvantageously defined interpolation points , the spline interpolation provides usable curve progressions and approximation properties ( Runge phenomenon ). The spline interpolation can be calculated with little, linear effort, but provides a lower order of convergence compared to the polynomial interpolation .
The template for the spline interpolation (third degree) is the traditional, flexible ruler used by shipbuilders , the straklatte (English spline ). This is fixed at any number of points specified by the designer and then connects the points with a smooth and harmonious bending line . The straightening bar thus creates the line through all points with minimal bending energy and the smallest of curvatures . While the turning points (places of maximum linearity and minimum bending energy) are usually between the support points in the Straklatte and the support points themselves are places of maximum curvature (places of maximum force through fixation), the turning points in the polynomial interpolation are close to the support points at which polynomial best approximation even in the support points.
The terms spline interpolation or spline function without further additions always designate the spline interpolation or spline function of the third degree. Both terms are mostly used synonymously. However, the term spline is increasingly used as an abbreviation for B-spline , and more rarely for other spline-like lines such as the Bézier curves .
Realities
Given: a natural number and support points
as well as function values . We are looking for a piecewise polynomial function, a spline ,





![{\ displaystyle S \ colon [x_ {0}, x_ {n}] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24a0db6b5bdb973da4643b4ae73a7a593d4154f7)
with for , with for the restrictions



![{\ displaystyle s_ {i}: = S | _ {[x_ {i}, x_ {i + 1}]} \; \ colon \; [x_ {i}, x_ {i + 1}] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb4de5789f3492286342a0015a4383d805fec8a5)
on which subintervals are polynomials.
![{\ displaystyle [x_ {i}, x_ {i + 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7138606cdb8eb7dddaba59b5aefe1ade6bc05a1b)
Linear (simple route)
The simplest method is to use straight lines between two neighboring points; the calculation of a simple spline as a segment is done in the same way as the graph between two points:

or

As mentioned above, these “simple” spline polynomials can be very imprecise. Cubic spline polynomials give considerably better results.
Cubic (3rd degree polynomials)
When connecting points with polynomials of a higher degree, properties must be defined in addition to the interpolation points, such as how the polynomials merge. For cubic splines, four coefficients have to be determined in one dimension and two further conditions have to be defined.
The cubic C² spline
C 2 demands that the composite function from all restrictions ( partial intervals ) is continuously differentiable twice. For this it is required that the first and second derivative of the restrictions at the support points


-
 and
and 
for match.

In principle, a change in an interpolation point always has a global effect on the entire spline , but the influence of the change is greatly attenuated with increasing distance - unlike with interpolation polynomials . Cubic splines are therefore less prone to overshooting.



The cubic C 2 spline fulfills a minimality property of the second derivative, which makes it particularly interesting compared to other interpolations.
construction
It can be seen that the second derivative of is a linear spline. This can therefore be described as described above using the following form:

-
 With
With 
for .
are the so-called moments , which correspond to the values of at the support points and are to be calculated in the following. Through double integration and skillful transformation, these equations result in third-degree polynomials with two further parameters and the form:





-
 .
.
The continuity conditions and to meet, we choose


-
 and .
and .
With this approach, the zeroth and the second derivatives of the restrictions at the support points already agree. The moments are to be selected so that the first derivatives at the support points are also the same. With

-
 and
and 
the following equations can be set up:
-
 for .
for .
Two equations are missing for and , which result from the boundary conditions .


This linear system of equations can also be expressed by the following, tridiagonal, strictly diagonally dominant matrix:

The values for depend on the boundary conditions.

To solve this, the complicated Gaussian algorithm can be dispensed with and z. For example, a simple forward pass can be used to eliminate the elements below the main diagonal with subsequent backward substitution ( Thomas algorithm ).
boundary conditions
In principle there is one interpolation interval less than support points ( fence post problem ). This means that two equations are missing to determine all the coefficients. These result from the boundary conditions. Typical boundary conditions are:
-
Natural boundary conditions (also free boundary)
-
Condition: ,


-
Meaning: The spline ends with turning points.
-
Calculation: and


-
Hermite boundary conditions (also clamped edge)
-
Condition: ,


-
Meaning: and are given, usually either by deriving a function to be interpolated or by an approximation of the same.



-
Calculation:

- periodic boundary conditions
-
Condition: interval , , ,
![{\ displaystyle [x_ {0}, x_ {n + 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32a24f5f02cd47e4ba3abc6dffd96b4ba951e8d3)



-
Meaning: Zero, first and second derivative of the beginning and the end of the interval are the same.

-
Calculation: An additional support point is introduced which limits the interval. However, the number of equations for calculating the moments and the size of the matrix remain the same, since it is already given so that the second derivatives agree. The following applies to the first and last row of the matrix:



- In addition, the corners of the matrix off the main diagonal are not zero here:

- The solution to this system is therefore more complicated. In the case of equidistant support points, a transformation can be used for this case .
- not-a-knot boundary conditions
-
Condition: ,


-
Meaning: The outer three points are each interpolated by a common polynomial, which can be done, for example, by equating the third derivatives. For splines up to and including four interpolation points, the not-a-knot spline therefore changes to a normal interpolation polynomial . The not-a-knot spline is used, for example, by the Matlab program .
-
Calculation: It applies . For the forward substitution, the boundary condition an is considered first. The following values can be used for this:



- If there is a division by zero and a limit value must be calculated up to the third row of the matrix (zero is the index of the first row / column):


- Only the sub-matrix is solved now beginning at and Randpolynom on the interval is determined by an additional polynomial interpolation so that , , , . is thereby already fulfilled.








- After the forward pass to eliminate the elements below the diagonal, the boundary condition an is now considered:


Other boundary conditions are common, such as integral boundary conditions or the symmetrical extension presented below.
Optimization of the computational effort
With equidistant support points with constant spacing , the system of equations is simplified to

-
 for .
for .
With the symmetrical extension and a so-called Tridiagonal-Toeplitz matrix is created , which can be solved particularly efficiently, also in parallel. For the right side, and can be used here . With can be written:






This has the inverse

with coefficients corresponding to the equations , the recursion and specifically of the formula





suffice.
Second derivative minimality property
Among all twice continuously differentiable functions that connect all support points within an interval , the cubic spline has the smallest curvature when using natural, periodic or Hermite boundary conditions: where here is any function on from C 2 that intersects all support points. It clearly follows that a glass of water that is too full on the table during a train journey "spills over the least" if the rail route has been parameterized using cubic splines.
![[a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![[a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
This so-called Holladay identity was proven by Holladay in 1957. Let the space of the twice differentiable functions be denoted, for which the zeroth and first derivatives are absolutely continuous and the second derivative is in . Let us now be an interpolating spline function for any function and the norm, then: with .
![{\ displaystyle C ^ {2} ([a, b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/854a57dd80b4ff52442e16e17f4a7f45a2281a9d)
![L ^ {2} ([a, b])](https://wikimedia.org/api/rest_v1/media/math/render/svg/9afbae301dd78d6739e6c45a942076bf669595e9)

![{\ displaystyle f \ in C ^ {2} ([a, b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/091bbfd527c5f82ec1a336d154239945837f63b1)




If the spline function fulfills the natural, periodic or complete boundary conditions, then :

This means that: 
Bicubic C 2 spline
The bicubic C 2 spline is the generalization of the simple, cubic C 2 spline to two dimensions; this is also referred to as multivariate interpolation . For this, the points to be interpolated z ij must be arranged in a rectangular grid. Each area A ij spanned between four points is characterized by a two-dimensional polynomial of 16 coefficients:

For a two-dimensional C 2 spline, the coefficients must be chosen in such a way that the function composed of all surfaces can be continuously differentiated twice in the x and y directions. That is, in addition to S itself, the following derivatives are continuous on whole :



construction

Illustration of the construction of a bicubic spline
It can be seen that every section through a partial surface parallel to the - or - axis provides a one-dimensional curve which can be described by a cubic polynomial of four coefficients. It follows that the four edges of each face are such polynomials. In order to obtain the required two-fold continuous differentiability, all points along the grid lines can first be interpolated one-dimensionally. The bicubic spline inherits the boundary conditions used for the one-dimensional splines.



Now available for each two-dimensional polynomial with coefficients 16 four-dimensional Randpolynome , , , each with 4 coefficients are available. The first index of the s indicates which axis they run parallel to.





In order to " add up" these boundary polynomials , a system of 16 linear equations must be set up. Four equations result from the requirement that S takes exactly the values at the grid points :



Another four equations result from the derivation of the boundary polynomials parallel to the -axis according to :



Another four equations from the derivation of the boundary polynomials parallel to the -axis according to :



The problem now arises that there are two points and two derivatives along each of the four edges. This means that a polynomial of degree 3 along the respective edge is actually fully specified. To accept z. B. the second derivatives at the corner points or further function values along the boundary polynomials would produce a linear dependence in the equation system. With the given equations, however, only 12 of the 16 coefficients can be determined. A non-linearly dependent system results from the addition of the mixed derivatives according to x and y. If this is set to approximately zero in the corner points, then it is only twice continuously differentiable in the corner points. However, there are jumps in the second derivatives along the edges. However, the mixed derivatives cannot be calculated directly from the boundary polynomials.

In order to obtain correct values for these mixed derivatives, which also provide continuous, second derivatives of along the edges , you can proceed as follows:

- Further, one-dimensional splines are formed along the grid lines, which run parallel to the axis


- Instead of the values, these interpolate the derivatives of other points of intersection with the grid lines



- The splines can now be derived from. This gives rise to the mixed derivatives



As with the one-dimensional C 2 spline, a change in a support point (data point) also generally affects all sub-areas in the bicubic spline. This illustrates why a construction based solely on the boundary polynomials and fails: These only change if a data value that is parallel (in - or - direction) to the sub-area under consideration is changed. In the figure on the right , a change in has no effect on the 1D splines that form the edge of . Only the renewed interpolation by creates a dependency between this point and the surface.







example
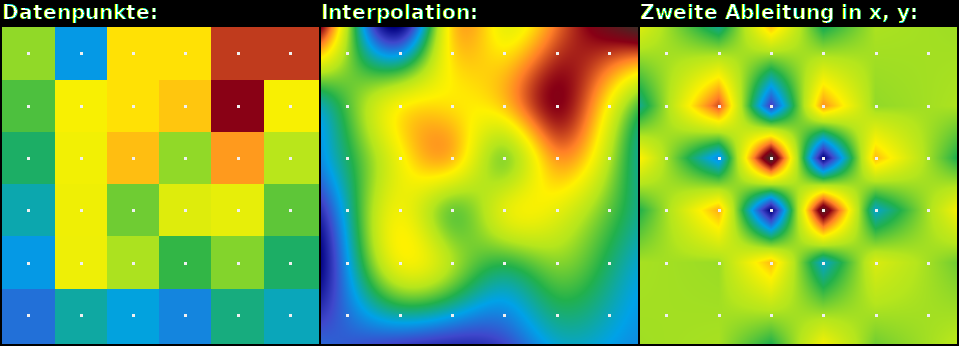
Example for bicubic interpolation: A data block of 6x6 values (left) is bicubically interpolated (middle). Natural boundary conditions were assumed (the second derivative on the boundary points is zero). The colors between the left and middle picture have been synchronized and describe the function values similar to the colors on a map to illustrate the altitude. To clarify the correctness of the interpolation, the second derivative is shown on the right . This consists of linear functions and is still continuous.

Interpolation with shape retention
Due to their properties, splines are widely used in CAD . The question arises under which conditions a spline interpolant inherits one of the following shape-retaining properties of the function to be interpolated :
![{\ displaystyle f \ colon [a, b] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
- Non-negativity: for everyone


-
Monotony : for


-
Convexity : for everyone and

![x, y \ in [a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e14f38807bc231b9e43d45c8e909d463afb17b5)
![\ lambda \ in [0, \, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcc8729134d189796d6917fb355ed7274283de87)
It can be seen here that classic splines have somewhat poorer properties than Bézier curves . The first question that arises is when an interpolating spline is convex.
For classical splines it is true that the set of possible splines on the interval to the grid is a finite-dimensional vector space . For the interpolation are (not necessarily with the grating coincident) node and associated ordinates predetermined and required that the spline continuously differentiable in and beyond to apply. If one additionally demands the convexity of the interpolating spline and minor technical assumptions, one finds that the set of all ordinate tuples for which such a spline exists is closed .
![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









This has far-reaching consequences. is a real subset of the if , since the input data need not be in a convex position. If a tuple is specified on the edge of , the set may have been abandoned due to calculation inaccuracies or other disturbances , so that no solution is found despite the solvability of the initial problem. The other implication of the theorem is even worse. For this purpose, five points are arranged in the form of the symbol " " so that the middle point is exactly on the tip. The only convex interpolator is then the absolute value function , and this is not continuously differentiable. So the 5-tuple belongs to the complement of , and this is open . Thus there is a neighborhood of the 5-tuple in which there are also no convex, continuously differentiable interpolators. If one shifts the middle point slightly upwards without leaving the environment, then one obtains five points in a strictly convex position, for which the interpolation problem still has no solution. Since this effect increases when many interpolation points are specified, there is only one way out to guarantee the solvability for input data in a strictly convex position, namely to violate the requirements of the sentence. The set from which the splines can be taken should not be a finite-dimensional vector space. The following are among others:







- (fractional) rational splines
- Splines with freely selectable intermediate nodes
- Exponential splines
- lacunar (patchy) splines
literature
- Stoer, Bulirsch: Numerical Mathematics 1 . 10th edition. Springer Verlag, Berlin, Heidelberg, New York 2007, ISBN 978-3-540-45389-5 , 2.5 Spline-Interpolation, pp. 112–148 (with examples, proofs, exercises and extensive information on other more specific literature).
Web links
Individual evidence
-
^ Robert Plato: Numerical Mathematics compact, 4th edition, page 27, remark 2.11
-
↑ Josef Stoer: Numerical Mathematics 1, 9th edition, section 2.4.2, page 109
-
↑ Lebesgue and Birkhoff: Handbook of Splines, Section 1.9, page 56
-
↑ John C. Holladay, 1928–1986. http://texts.cdlib.org/view?docId=hb767nb3z6&doc.view=frames&chunk.id=div00051&toc.depth=1&toc.id=
-
↑ Lebesgue and Birkhoff: Handbook of Splines, Section 2.2, page 82
-
↑ The example interpolation was created with: Program Numeric Collection by Mitja Stachowiak
-
↑ Jochen W. Schmidt: Staircase Algorithm and Construction of Convex Spline Interpolants up to the Continuity Computers and Mathematics with Applications, Volume 31, Number 4, February 1995, pp. 67-79.






![{\ displaystyle S \ colon [x_ {0}, x_ {n}] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24a0db6b5bdb973da4643b4ae73a7a593d4154f7)



![{\ displaystyle s_ {i}: = S | _ {[x_ {i}, x_ {i + 1}]} \; \ colon \; [x_ {i}, x_ {i + 1}] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb4de5789f3492286342a0015a4383d805fec8a5)
![{\ displaystyle [x_ {i}, x_ {i + 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7138606cdb8eb7dddaba59b5aefe1ade6bc05a1b)






































![{\ displaystyle [x_ {0}, x_ {n + 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32a24f5f02cd47e4ba3abc6dffd96b4ba951e8d3)






































![[a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\ displaystyle C ^ {2} ([a, b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/854a57dd80b4ff52442e16e17f4a7f45a2281a9d)
![L ^ {2} ([a, b])](https://wikimedia.org/api/rest_v1/media/math/render/svg/9afbae301dd78d6739e6c45a942076bf669595e9)
![{\ displaystyle f \ in C ^ {2} ([a, b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/091bbfd527c5f82ec1a336d154239945837f63b1)































![{\ displaystyle f \ colon [a, b] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)




![x, y \ in [a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e14f38807bc231b9e43d45c8e909d463afb17b5)
![\ lambda \ in [0, \, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcc8729134d189796d6917fb355ed7274283de87)












