Idealized greenhouse model

The idealized greenhouse model is a simple model for determining the surface and atmospheric temperature of the earth or another planet. The greenhouse effect can be illustrated with the help of an idealized planet ; this model is common in relevant textbooks.

overview

→ Main article : greenhouse effect

Central condition of the greenhouse effect, shown using the example of the planet earth: The wavelength distribution of the radiation coming from the sun differs from the infrared radiation as it is emitted by the earth (here as an example for three temperature values ​​of the earth). Below it is shown which parts of the atmosphere filter out which spectral range.

The surface of the sun emits electromagnetic waves in the visible range and beyond, something as thermal radiation . The radiation corresponds to that of a body at an effective temperature of approx. 5,500 ° C. The earth is considerably colder and radiates - as Planck's law of radiation describes it - at considerably longer wavelengths, especially in the infrared range. The idealized greenhouse model is based on the fact that certain gases in the earth's atmosphere are transparent to short-wave electromagnetic sun rays (such as visible light), but are not very permeable to long-wave heat radiation emitted by the earth's surface. These gases include B. carbon dioxide and water vapor . So heat can easily penetrate into the atmosphere, but is partly retained there. This has a lasting effect on the earth's radiation budget.

The Kirchhoff's radiation law states that any body in thermal equilibrium is, the absorbed energy again he must emit. An isotropic body radiates equally in all directions. Consequently, the atmosphere in the long-wave infrared range also radiates towards the ground, which is known as atmospheric counter-radiation . In this model, the greenhouse gases heat the planet's surface to a higher temperature than would be observable without them. This temperature offset leads to increased radiation, until finally the initially retained part of the radiated heat is also radiated at the top of the atmosphere.

The model planet

The following simplified assumptions are made and sizes are considered for the model planet:

• The planet is perfectly spherical.
• The planet receives radiation (sunlight) that is constant over time from its central star.
• S ₀ denotes the solar constant of the planet. This indicates the irradiance for sunlight that hits the planet's surface exactly perpendicularly.
• The planet has an albedo that is independent of place and time , which is also assumed to be independent of the wavelength of the incident sunlight.
• α _P denotes the albedo of the planet.
• T _s denotes the temperature of the planet's surface - this is assumed to be constant everywhere. The index s stands for surface .
• T _a denotes the temperature of the planet's atmosphere - this is also assumed to be constant everywhere.
• The planet is in equilibrium with regard to radiation and temperature: Depending on the amount of radiation received, the two temperatures T _s and T _{a have} adjusted accordingly.

In equilibrium values are for T _s and T _a , so that the output from the top of the atmosphere radiated power equal to the power absorbed by the atmosphere radiant power. The incoming sunlight is short-wave and the radiation emitted by the planet is long-wave. Both radiation currents have their own different emission and absorption characteristics.

In the idealized model, we also assume that the atmosphere is completely transparent to sunlight and the surface has an emissivity of 1 for long-wave radiation , i.e. is a black body . As mentioned above, according to Kirchhoff's law of radiation, the degree of absorption of the atmosphere is equal to its emissivity at every wavelength. The radiation emitted by the surface of the planet can show a slightly different spectral composition compared to the atmosphere. In the model it is assumed that the mean emissivity (= degree of absorption) of both jet streams is identical when interacting with the atmosphere. Consequently, the symbol ε stands for the degree of emission and absorption of each infrared radiation stream in the atmosphere.

Model calculation

The planet with its surface was assumed to be a black body; According to the Stefan-Boltzmann law, the surface emits a radiation flux of

${\displaystyle F=\sigma \,T_{s}^{4}}$,

where σ is the Stefan-Boltzmann constant with a value of ; it is a derived natural constant. ${\displaystyle \sigma \approx 5{,}670\,374\cdot 10^{-8}\,{\frac {\mathrm {W} }{m^{2}K^{4}}}}$

For the total surface emission, the above formula has to be multiplied by the planet surface. In the following, we will dispense with this in favor of simpler formulas and focus on the emission per square meter of the surface ("radiation density").

For the radiation density of the infrared radiation emitted from the atmosphere into space, we set up the following balance equation - both textually and as a formula:

(1)	Total radiation of the atmosphere upwards = radiation of the atmosphere upwards + part of the radiation from the earth's surface that is not absorbed by the atmosphere
	${\displaystyle F_{\uparrow }=\varepsilon \sigma T_{a}^{4}+(1-\varepsilon )\sigma T_{s}^{4}}$

In the second summand, ε is the portion of the radiation leaving the surface that is absorbed, i.e. the degree of absorption of the atmosphere. In the first summand, ε is the emissivity of the atmosphere, the adaptation of the Stefan-Boltzmann law in order to do justice to the fact that the atmosphere is not optically dense. Here another simplification has an effect in the idealized model: We assume implicitly that the atmosphere is an infinitesimally thin layer around the planetary surface, so that the radiating surface of the atmosphere is exactly the same as the planetary surface itself.

So that the net radiation flux at the top of the atmosphere disappears, the following equality must be given:

(2)	Radiation from the sun = radiation of the atmosphere upwards + part of the radiation from the planet's surface that is not absorbed by the atmosphere
	${\displaystyle {\frac {S_{0}}{4}}(1-\alpha _{p})=\varepsilon \sigma T_{a}^{4}+(1-\varepsilon )\sigma T_{s}^{4}}$

The flux density of incident solar radiation is specified by the solar constant S ₀ . Since the surface of the idealized planet as a sphere is four times its cross section (also: shadow), the surface-related incident radiation is S _0/4 . The planetary albedo α _P is the part of incident solar radiation that is reflected back into space. It does not matter to which parts the reflection occurs on the planet's surface or on the top of the atmosphere.

In order for the net radiation flux to disappear on the planet's surface, the following must be given:

(3)	Radiation of the planet's surface = radiation from the sun + radiation from the atmosphere downwards
	${\displaystyle \sigma T_{s}^{4}={\frac {S_{0}}{4}}(1-\alpha _{p})+\varepsilon \sigma T_{a}^{4}}$

An energy balance of the atmosphere can be derived by substituting (2) into (3):

(4)	Radiation of the planet's surface = total radiation of the atmosphere
	${\displaystyle \varepsilon \sigma T_{s}^{4}=2\varepsilon \sigma T_{a}^{4}}$

Note the important factor 2, which results from the fact that the atmosphere radiates both upwards and downwards.

This equation can be solved for T _a :

 (5)   ${\displaystyle T_{a}={\frac {T_{s}}{2^{1/4}}}\approx {\frac {T_{s}}{1{,}189}}}$

For our idealized model, the ratio of the two temperatures is completely independent of ε, the degree of absorption of the atmosphere.

With (5) inserted in (2) one obtains a solution for T _s as a function of the input parameters:

${\displaystyle {\frac {S_{0}}{4}}(1-\alpha _{p})=\left(1-{\frac {\varepsilon }{2}}\right)\sigma T_{s}^{4}}$

or changed:

 (6)   ${\displaystyle T_{s}=\left({\frac {S_{0}(1-\alpha _{p})}{4\sigma \left({1-{\frac {\varepsilon }{2}}}\right)}}\right)^{1/4}}$

An effective temperature T _e can also be given for the entire system of the planet (which we assumed above to be a black body) and its atmosphere, the total radiation of which we referred to above with . This is the temperature that characterizes the radiance , assuming that the planet including its atmosphere as a complete system would be a perfect emitter . In the idealized model this is easy to represent: T _e is also the solution for T _s for the case of ε = 0, i.e. a missing atmosphere. In this case (6) simplifies to (7): ${\displaystyle F_{\uparrow }}$ ${\displaystyle F_{\uparrow }}$ ${\displaystyle F_{\uparrow }=\sigma T_{e}^{4}}$

(7)   ${\displaystyle T_{e}=\left({\frac {S_{0}(1-\alpha _{p})}{4\sigma }}\right)^{1/4}}$

The effective temperature T _{e determined in} this way results in (6):

(8th)   ${\displaystyle T_{s}={\frac {1}{\left(1-{\frac {\varepsilon }{2}}\right)^{1/4}}}\,T_{e}}$

Application to the planet earth

Idealized greenhouse model with isothermal atmosphere. The blue arrow marks short-wave solar radiation flux, the red arrow represents the long-wave radiation flux emitted by the planet. The beam currents are shown laterally offset in the graphic for better visualization; in the model, both take place in the same place. The atmosphere is shown as a layer between the dashed lines; it only interacts with long-wave infrared radiation. A special solution was given for the values ​​ε = 0.78 and α _p = 0.3. She represents the planet earth. The numbers in brackets are the flux densities in percent of S _0/4 .

The equilibrium solution with ε = 0.82. An increase by Δε = 0.04 corresponds to a doubling of the carbon dioxide concentration and the associated water vapor feedback

The equilibrium solution without the greenhouse effect: ε = 0

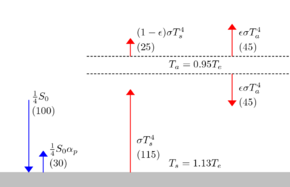
On planet earth, the solar constant and the albedo are on average around . ${\displaystyle S_{0}=1366\;\mathrm {W} /\mathrm {m} ^{2}}$ ${\displaystyle \alpha _{p}=0{,}3}$

Model results

In the case of a perfect greenhouse where no radiation can escape from the surface, i.e. ε = 1, with (6):

${\displaystyle {\begin{aligned}T_{s}&=303~\mathrm {K} =30~{}^{\circ }\mathrm {C} \\T_{a}&=254~\mathrm {K} =-19~{}^{\circ }\mathrm {C} \end{aligned}}}$

For the global average surface temperature T _s , an estimated value of around 288 K, i.e. around 15 ° C, is known. To set this, one varies the parameter ε. For ε = 0.78, which means that 22 percent of the radiation emitted by the surface escape directly into space, the following applies with (6):

${\displaystyle {\begin{aligned}T_{s}&=288{,}3~\mathrm {K} =15{,}1~^{\circ }\mathrm {C} \\T_{a}&=242{,}5~\mathrm {K} =-30{,}7~^{\circ }\mathrm {C} \end{aligned}}}$.

The associated effective temperature is given by equation (8) as

${\displaystyle T_{e}=255~\mathrm {K} =-18~{}^{\circ }\mathrm {C} }$

Change in temperature due to radiative forcing

The radiative forcing resulting from a doubling of the atmospheric carbon dioxide concentration is 3.71 W / m ² with simple parameterization. This is also the value given by the IPCC .

From the equation for (1) it follows: ${\displaystyle F_{\uparrow }}$

${\displaystyle \Delta F_{\uparrow }=\Delta \varepsilon \left(\sigma T_{a}^{4}-\sigma T_{s}^{4}\right)}$

With the values ​​of T _s and T _a for ε = 0.78 we get for with Δε = 0.019. Hence, a change in ε from 0.78 to 0.80 is in agreement with the radiative forcing that arises from the doubling of the carbon dioxide concentration. For ε = 0.80: ${\displaystyle \Delta F_{\uparrow }=-3{,}71\;\mathrm {W} /\mathrm {m} ^{2}}$

${\displaystyle T_{s}=289{,}5~\mathrm {K} }$

Consequently, this model predicts a global warming of ΔT _s  = 1.2 K for a doubling of the carbon dioxide concentration. A prediction of a typical climate model results in a warming of the earth's surface by 3 K. This is primarily due to the fact that climate models take into account the positive feedback that primarily results from the water vapor feedback . This effect can be taken into account with a simple trick. For this purpose, Δε is increased by 0.02 to a total of Δε = 0.04. In this way, the effect of an increased water vapor concentration triggered by the heating is approximately taken into account. This idealized model then predicts global warming of ΔT _s  = 2.4 K for a doubled carbon dioxide concentration , which roughly agrees with the information provided by the IPCC.

Evaluation of the model assumptions for the earth

The assumption of the perfect spherical shape is considered a good approximation for the earth.

The assumption of constant solar radiation in combination with the planet-wide constancy of a uniform surface and atmospheric temperature T _a and T _s , on the other hand, is far removed from the real conditions on earth. As a justification for the idealized model, it is stated that temperature differences on earth are equalized by convection . On the earth's surface, this happens, for example, through the presence of ocean currents, which lead to strong mixing.

Nevertheless, the conditions on earth are significantly different from the ideal:

• The so-called solar constant fluctuates, especially as a result of the sunspot cycle .
• The solar radiation on every point of the earth varies greatly according to the rotation of the earth around the sun and its precession in the course of the day and year.
• A mixing of the temperatures takes place only very imperfectly:
  • For example, it is much warmer on the earth's surface in the equatorial zone than in the polar zones all year round.
  • The biosphere, especially the flora, contributes considerably to temporal fluctuations; For example, plant growth influences the albedo and the CO ₂ content of the atmosphere and the evaporation capacity of the vegetation influences the water cycle in the atmosphere.
  • When the sun is shining, for example, the sandy bottom heats up considerably, but the sea surface only slightly warms up.
  • In the atmosphere, warm and cold layers alternate, the temperature of which is only mixed to a very limited extent due to effects such as the weather.

Variants and extensions

Alternatively, instead of the surface temperature and the atmospheric temperature, a pair consisting of the atmospheric temperature of a lower and an upper atmospheric temperature can be considered in the idealized greenhouse model shown.

The single-layer atmosphere model shown can be converted directly into a multi-layer atmosphere model. To do this, the equations for the temperatures must be converted into a series of coupled equations for the individual layers. This simple model always predicts a temperature that decreases with increasing altitude and the temperature of all layers increases with increasing greenhouse gas concentration. None of these assumptions are realistic for the earth: In the earth's atmosphere the temperatures rise above the tropopause and when the greenhouse gas concentration increases it is expected and observed that the temperatures there (in the stratosphere) decrease. The reason is that the earth's atmosphere does not have the same transmissivity for all optical wavelength ranges .

literature

• Craig F. Bohren, Eugene E. Clothiaux: Fundamentals of Atmospheric Radiation . John Wiley & Sons, Chichester 2006, ISBN 3-527-40503-8 , 1.6 Emissivity and Global Warming, pp. 31-41 (English).
• Grant W. Petty: A First Course in Atmospheric Radiation . 2nd Edition. Sundog Pub, Madison, Wisconsin 2006, ISBN 0-9729033-1-3 , 6.4.3 Simple Radiative Models of the Atmosphere, pp. 139-143 (English).

Individual evidence

1. ↑ Chapter 2, The global energy balance (PDF; 654 kB), UT course Physical Climatology
2. ↑ What is the Greenhouse Effect? (PDF; 1.9 MB) Intergovernmental Panel on Climate Change. 2007. Retrieved March 12, 2013.
3. ↑ Stefan-Boltzmann constant. National Institute of Standards and Technology, accessed July 20, 2019 . 
4. ↑ R. Gieré, Peter silence: Energy, Waste and the Environment: A Geochemical Perspective . Geological Society of London, 2004, ISBN 1-86239-167-X , pp. 162 (English, limited preview in Google Book Search).
5. ^ J. Hansen, D. Johnson, A. Lacis, S. Lebedeff, P. Lee, D. Rind, G. Russell: Climate Impact of Increasing Atmospheric Carbon Dioxide . In: Science . tape 213 , no. 4511 , August 28, 1981, p. 957 , doi : 10.1126 / science.213.4511.957 ( atmos.washington.edu archived at web.archive.org [PDF; accessed June 23, 2019]).
6. ↑ BD Santer, JF Painter, C. Bonfils, CA Mears, S. Solomon, TML Wigley, PJ Gleckler, GA Schmidt, C. Doutriaux, NP Gillett, KE Taylor, PW Thorne, FJ Wentz: Human and natural influences on the changing thermal structure of the atmosphere . In: Proceedings of the National Academy of Sciences . tape 110 , no. 43 , October 22, 2013, p. 17235 , doi : 10.1073 / pnas.1305332110 .

Web links

• R. Tuckermann: Atmospheric chemistry script (PDF; 1.8 MB)
• Lectures by David Archer : Our First Climate Model and The Greenhouse Effect (English)