Involute

Two involutes (red) of a parabola

The involute (also involute ) is a term from the mathematical sub-area of differential geometry . Each rectifiable curve is assigned a family of curves other than its involute , which result from the "development" of its tangent .

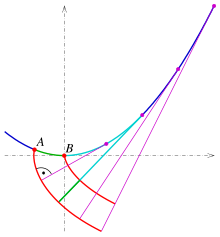
The involute can be shown clearly as a thread line: A flat body, one side of which has the shape of the initial curve, is placed on a sheet of paper. A thin thread is wrapped around the exit curve and stretched taut. A pen is attached to the outer end of the thread, the tip of which rests on the paper. Then the thread is slowly unwound from the curve, always keeping it taut. The curve that appears on the paper is an involute.

Since the thread can initially have any length, there are infinitely many involutes for every curve, all of which run parallel to each other, that is: If two involutes are given, then every normal of one is also normal of the other, and all of these normal are between the two involutes of the same length. Every normal of an involute is therefore normal of all involutes. The normals of the involutes are simply the tangents of the given curve. This is the envelope of the involute normals. Mostly with involute the circle involute is meant; however, this is only a special case of the general involute.

Involute of a parameterized curve

Describes a regular curve in the Euclidean plane, the curvature of which is nowhere 0 and is , then the corresponding curve is with the parametric representation ${\displaystyle {\vec {x}}={\vec {c}}(t),\;t\in [t_{1},t_{2}]}$ ${\displaystyle a\in (t_{1},t_{2})}$

• ${\displaystyle {\vec {X}}={\vec {C}}_{a}(t)={\vec {c}}(t)-{\frac {{\vec {c}}'(t)}{|{\vec {c}}'(t)|}}\;\int _{a}^{t}|{\vec {c}}'(w)|\;\mathrm {d} w}$

an involute of the given curve.
The integral describes the acute length of the unwound thread of the curve in the interval and the vector in front of it is the tangent unit vector. If you add any fixed number to the integral , you get an involute with a longer thread. So: The thread length and thus the involute can not only be varied with the parameter , but also by adding a number to the integral (see example Neil's parabola ). ${\displaystyle [a,t]}$ ${\displaystyle l_{0}}$ ${\displaystyle l_{0}}$ ${\displaystyle a}$ ${\displaystyle l_{0}}$

Is so is ${\displaystyle {\vec {x}}={\vec {c}}(t)=(x(t),y(t))^{T}}$

${\displaystyle {\begin{aligned}X(t)&=x(t)-{\frac {x'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(w)^{2}+y'(w)^{2}}}\,\mathrm {d} w\\Y(t)&=y(t)-{\frac {y'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(w)^{2}+y'(w)^{2}}}\,\mathrm {d} w\;.\end{aligned}}}$

Properties of the involute

Involute: properties

In order to derive properties of a regular curve it is advantageous to use the arc length of the given curve as a parameter . Because then applies and , where is the curvature and the unit normal. For the involute we get: ${\displaystyle s}$ ${\displaystyle \;|{\vec {c}}'(s)|=1\;}$ ${\displaystyle \;{\vec {c}}''(s)=\kappa (s){\vec {n}}(s)\;}$ ${\displaystyle \kappa }$ ${\displaystyle {\vec {n}}}$

${\displaystyle {\vec {C}}_{a}(s)={\vec {c}}(s)-{\vec {c}}'(s)(s-a)\;}$ and

${\displaystyle {\vec {C}}_{a}'(s)=-{\vec {c}}''(s)(s-a)=-\kappa (s){\vec {n}}(s)(s-a)\;.}$

It follows from this:

• The involute is not regular at the point (it is ), ${\displaystyle {\vec {C}}_{a}(a)}$ ${\displaystyle |{\vec {C}}_{a}'(a)|=0}$

and it follows: ${\displaystyle \;{\vec {C}}_{a}'(s)\cdot {\vec {c}}'(s)=0\;}$

• The normal of the involute at the point is the tangent of the given curve at the point and ${\displaystyle {\vec {C}}_{a}(s)}$ ${\displaystyle {\vec {c}}(s)}$
• the involutes are parallel curves , da and the unit normal is in. ${\displaystyle {\vec {C}}_{a}(s)={\vec {C}}_{0}(s)+a{\vec {c}}'(s)}$ ${\displaystyle {\vec {c}}'(s)}$ ${\displaystyle {\vec {C}}_{0}(s)}$

The last property suggests the following strategy for determining the involutes of a curve:

1. Use a parametric representation of the given curve that allows the simplest possible antiderivative of the integral to be solved.
2. Think for which initial parameter and / or which thread extension the integral will be simple. ${\displaystyle a}$ ${\displaystyle l_{0}}$
3. If one finds an involute that is easy to describe in this way, then all involutes result as parallel curves thereof.

Examples

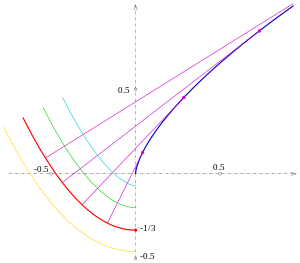
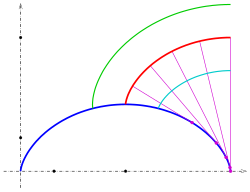
Involute of a circle

Involute of a circle

→ Main article : Circular volvents

For the circle with the parametric representation is and thus . The integral has the value . So the equations of the involute are: ${\displaystyle \;(r\cos(t),r\sin(t))\;}$ ${\displaystyle {\vec {c}}'(t)=(-r\sin t,r\cos t)^{T}}$ ${\displaystyle |{\vec {c}}'(t)|=r}$ ${\displaystyle r(t-a)}$

• ${\displaystyle X(t)=r(\cos t+(t-a)\sin t)}$

${\displaystyle Y(t)=r(\sin t-(t-a)\cos t)}$

In the drawing the involutes for (green), (red), (magenta) and (cyan) are drawn. The involutes are similar to an Archimedean spiral , but they are not. ${\displaystyle a=-0{,}5}$ ${\displaystyle a=0}$ ${\displaystyle a=0{,}5}$ ${\displaystyle a=1}$

For the arc length of the involute with results ${\displaystyle 0\leq t\leq t_{2}}$

${\displaystyle L={\frac {r}{2}}{t_{2}}^{2}\;.}$

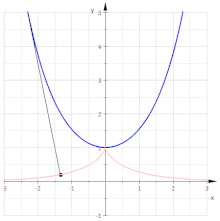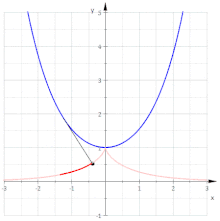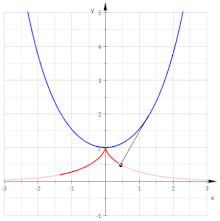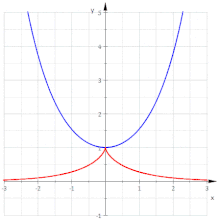
Involute of a Neil parabola

Involute of a neilian parabola (blue). Only the red curve is a parabola.

The parametric representation describes a Neil parabola . Because is and . If you lengthen the thread by the calculation becomes simple and it results ${\displaystyle \;{\vec {c}}(t)=({\tfrac {t^{3}}{3}},{\tfrac {t^{2}}{2}})^{T}\;}$ ${\displaystyle \;{\vec {c}}'(t)=(t^{2},t)^{T}\;}$ ${\displaystyle \;|{\vec {c}}'(t)|=t{\sqrt {t^{2}+1}}}$ ${\displaystyle \int _{0}^{t}w{\sqrt {w^{2}+1}}\;\mathrm {d} w={\frac {1}{3}}{\sqrt {t^{2}+1}}^{3}-1/3}$ ${\displaystyle l_{0}=1/3}$

${\displaystyle X(t)=\;\cdots \;=-{\frac {t}{3}}}$

${\displaystyle Y(t)=\;\cdots \;={\frac {t^{2}}{6}}-{\frac {1}{3}}\ .}$

Elimination of the parameter yields the parabola with the equation So: ${\displaystyle t}$ ${\displaystyle \;Y={\frac {3}{2}}X^{2}-{\frac {1}{3}}\;.}$

• The involutes of Neil's parabola are parallel curves of the parabola ${\displaystyle \;({\tfrac {t^{3}}{3}},{\tfrac {t^{2}}{2}})\;}$ ${\displaystyle \;y={\frac {3}{2}}x^{2}-{\frac {1}{3}}\;.}$

(Note: The parallel curves of a parabola are no longer parabolas!)

Note: Calculating the evolute of the parabola results in Neil's parabola again (see section involute and evolute .) ${\displaystyle \;y={\frac {3}{2}}x^{2}-{\frac {1}{3}}\;}$ ${\displaystyle \;({\tfrac {t^{3}}{3}},{\tfrac {t^{2}}{2}})\;}$

The red involute of a chain line (blue) is a tractrix.

Involute of the chain line

For the chain line we get and because of is and This gives the parametric representation of the involute: ${\displaystyle \;(t,\cosh t)\;}$ ${\displaystyle \;{\vec {c}}'(t)=(1,\sinh t)^{T}\;}$ ${\displaystyle \;\cosh ^{2}t-\sinh ^{2}t=1\;}$ ${\displaystyle \;|{\vec {c}}'(t)|=\cosh t}$ ${\displaystyle \;\int _{0}^{t}\cdots =\sinh t\;.}$

${\displaystyle (t-\tanh t,1/\cosh t)\;.}$

This is the parameter representation of a Traktrix . The following applies:

• The involutes of the chain line are parallel curves of the Traktrix ${\displaystyle \;(t,\cosh t)\;}$ ${\displaystyle (t-\tanh t,1/\cosh t)\;.}$

Involute of a cycloid

Involute of a cycloid (blue): Only the red curve is a cycloid again.

The parametric representation describes a cycloid . Because is and . (Some trigonometric formulas were used.) It results ${\displaystyle \;{\vec {c}}(t)=(t-\sin t,1-\cos t)^{T}\;}$ ${\displaystyle \;{\vec {c}}'(t)=(1-\cos t,\sin t)^{T}\;}$ ${\displaystyle \;|{\vec {c}}'(t)|=\cdots =2\sin {\frac {t}{2}}}$ ${\displaystyle \int _{\pi }^{t}2\sin {\frac {w}{2}}\;\mathrm {d} w=-4\cos {\frac {t}{2}}}$

${\displaystyle X(t)=\;\cdots \;=t+\sin t}$

${\displaystyle Y(t)=\;\cdots \;=3+\cos t\ .}$

These equations describe the shifted cycloid shown in the picture (red).
So:

• The involutes of the cycloids are parallel curves of the cycloids ${\displaystyle \;(t-\sin t,1-\cos t)\;}$

${\displaystyle (t+\sin t,3+\cos t)\;.}$

Involute and Evolute

The evolute of a given curve consists of the centers of curvature of . The connection between evolute and involute is as follows: ${\displaystyle k_{0}}$ ${\displaystyle k_{0}}$

• Each curve is the evolute of each of its involutes.

Because of this correlation, the involute is sometimes involute called.

Applications

technology

In engineering , the involute is particularly important in the construction of gear wheels and racks . With the involute gearing , which is often used , the cross-section of a tooth flank is part of an involute of a circle . This ensures that engaged teeth touch along a straight line of action (the tangent to the base circles). The involute shape is easier to manufacture than the cycloid shape of the tooth flank, which is also used .

medicine

The term can also be found in the field of medicine . The involutes of the spirally curved femoral condyles in the knee joint and their intersection points of the transverse axes of movement, which can therefore be found on the resulting evolute, are important in understanding the biomechanics of the knee and knee-specific joint properties.

Sports

In athletics , the starting lines on a 400-meter lane are calculated using the involute so that runners on the outer lanes cover the same distance as runners on the inner lanes. This applies in particular to the 200 and 400 meter races , the sprint relays and the long-distance competitions.

literature

• K. Burg, H. Haf, F. Wille, A. Meister: Vector analysis: Higher mathematics for engineers, natural scientists and… Springer-Verlag, 2012, ISBN 3834883468 .
• Small encyclopedia of mathematics. Harry Deutsch Verlag, 1977, ISBN 3 87144 323 9 , p. 475.
• A. Ostrowski: Evolute, involute and parallel curves. Springer, Basel 1972, ISBN 978-3-0348-5528-0 .

Individual evidence

1. ↑ K. Burg, H. Haf, F. Wille, A. Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und ... Springer-Verlag, 2012, ISBN 3834883468 , p. 30.
2. ^ R. Courant: Lectures on differential and integral calculus, 1st volume. Springer-Verlag, 1955, p. 267.