Chain line (math)
A chain line (also rope curve , catenoide or chain curve , English catenary or funicular curve ) is a mathematical curve that describes the slack of a chain suspended at its ends under the influence of gravity . It is an elementary mathematical function, the hyperbolic cosine , or cosh for short .
Mathematical description
The calculation of the chain line is a classic problem of the calculus of variations . Imagine a rope of a certain size and length that is suspended at its ends. The rope curve is the result of the smallest possible potential energy of the rope. One tries to understand this mathematically.
For this one needs the mathematical expression for the potential energy. It is a refinement of the well-known “weight times height” . The refinement consists in that the energy for "all parts" of the rope is evaluated separately and added up at the end. This is necessary because the parts of the rope are at different heights. The mental division of the rope into smaller and smaller parts turns the sum into an integral. The height from is replaced by the function you are looking for, the mass by the mass of the piece of rope over the interval ; according to Pythagoras this is:
where the mass is per meter. If the rope is hung up at the points , the energy (“weight times height”) results as
A similar consideration leads to the expression for the length of the rope:
The energy must be minimized, but the length is specified. You bring this under one roof with a Lagrange multiplier , that is, you minimize the expression
The variation gives the differential equation (Euler-Lagrange equation):
Interestingly, both the mass size and the gravitational acceleration dropped out in this step . A heavy rope takes on the same shape as a light one, and on the moon it has the same shape as on earth, despite different gravitational acceleration.
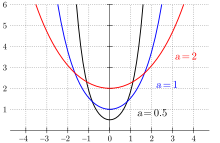
The solutions to the equation are the functions
These are enlarged and shifted hyperbolic cosine functions. is the radius of curvature at the vertex (see illustration) and at the same time the magnification factor. is the shift in the direction, the shift in the direction.
The concrete form which takes the rope ultimately be calculated by , and adapts that the curve passes through the suspension points and the predetermined length has.
example
As an example, a rope of the length suspended between two posts (distance ) is given (see illustration ). The posts are the same height and are located at and , so it applies .
To calculate the radius of curvature , we write the rope length as a function of :
- .
This relationship clearly defines depending on and . Since it is not possible to give a closed expression for , the value must be calculated approximately using a numerical method for solving nonlinear equations.
However, if and are given, and can be represented as closed as follows . Is the square of the equation (above) (below mentioned) by the square of the equation is subtracted, then gives the resultant to the difference equation , resulting due eliminated and after can be changed. Inserting this in and transformations result in the desired expression for the distance in closed form z. B.
or
- .
Finally, one reads the condition from the figure from which one obtains. The relationships also apply
where the "slack" is.
The potential energy of this system is
- .
More precisely, this is the energy difference compared to the case where the rope is completely at the same height as the suspension points ( ).
With the help of the energy one can calculate the force in the suspension points. To do this, imagine that the rope runs at a suspension point over a pulley that diverts the force in a horizontal direction. In order to pull the rope out a very small distance as shown , one has to expend the energy . This can be calculated and thus receives the force . To calculate , the energy of the original rope is compared with that of the shortened rope. The result is surprisingly simple, namely
with . The same formula can be applied to sections of the rope. Since the sections all have the same radius of curvature , but the sag is negligible for small sections (down in the valley) , there is tension in the rope in the valley of the rope .
If you put the posts close together, the slack dominates , which is then exactly half the pitch. As expected, the force is then half the weight of the rope (note that two suspension points share the load).
The formula also shows how the force with increasing rope tension exceeds half the weight by a factor . The factor is practically 1 for very small radii of curvature , but approximately or also for very large radii of curvature.
In everyday life the factor is around 2 to 4. The whole or double the weight of the rope then acts at the suspension point.
Relationships with other functions

m (0) = 1/2 , c (0) = 2 : The indefinite expression 0/0 in this case is 1/2 or 2.
parabola
In 1639 Joachim Junge proved that the chain line is not a parabola . Gottfried Leibniz , Christiaan Huygens and Johann I Bernoulli found out in 1690/91 how the chain curve should be formed. The parabola occurs with a line load evenly distributed over the span x , e.g. B. a suspension bridge in which the weight of the ropes can be neglected compared to that of the roadway. The figure on the right compares the curve of a chain line (red) with a normal parabola (green).
Catenoid
By rotation of the chain line about the x generated axis rotation surface is used as a catenoid referred to and is a minimal surface .
Traktrix
The chain line is the evolution to the Traktrix (drag curve).
Examples
For = 100 m and a pole distance of 200 m (that is a special case ), a 2 x 117.5 m long rope needed: . The sag is 54 m. For a steel cable with a cross-section of 100 cm², one half of the cable weighs 9.2 t. The corresponding weight force of 9 · 10 4 N is the vertical force on a suspension. The horizontal force on a suspension is 7.7 · 10 4 N.
If about 20.2% of the total width , the sag is equal to the width (square overall dimensions). This is the case, for example, with the Gateway Arch (see below in the Architecture section ), which is 630 feet wide and just as high. The exact formula
with a = 127.7 feet and w / 2 = 315 feet is exhibited inside the monument.
Applications in architecture
An analog of the catenary support line followed by the shear forces free sheet :
- The Nubian barrel , a barrel vault , is a variant of the Nubian vault , a clay vault construction without formwork and often without gauges, which takes its name from traditional construction forms in Nubia. In order to achieve the greatest possible stability, the support line usually follows the chain line.
- An early European example is the 30,80 m diameter dome of St Paul's Cathedral in London , which was built after 1666 according to plans by Christopher Wren . He had a catenoid placed between an outer and an inner wooden hemisphere, which took up the weight of the lantern but also made it possible to reduce the structural weight. At that time the curve was approximated empirically.
- Auguste de Montferrand transformed the dome of Wren in St. Paul's Cathedral in the construction of the iron dome of St. Isaac's Cathedral in St. Petersburg (1838–1841) and used iron as a new medium in construction. Montferrand's iron dome itself became the model for the iron dome of the Capitol in Washington (1855–1866).
- Cross-section of the roof of the Budapest Ost (Keleti) train station (Hungary) forms a chain line. Built from 1881/84. Designer: János Feketeházy .
- Antoni Gaudí used the construction principle based on it more often, including for the Sagrada Família in Barcelona. The model of the similar church of Colònia Güell was also determined empirically, namely "upside down" by hanging cords with appropriate weights (around 1900; original lost in a fire)
- The supporting line of the 192 m high Gateway Arch in St. Louis (2018) is not a real chain line due to the varying thickness of the arch.
photos
Sheffield Winter Garden
Cross section of the roof of the Eastern Railway Station in Budapest (Hungary)
Drawing by Christiaan Huygens
The ropes of overhead lines follow the chain line
Three chains surround a chain line figure (analogous to the Arbelos )






![[x, x + \ mathrm dx]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2497bba0513a671ec5bbc5074589b01eb03b3374)
































































