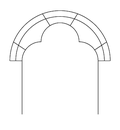
Arch (architecture)

Carrying arch above the portal, next to it incomplete blind arches
In architecture, an arch is a component used to bridge openings in the masonry . An arch without a load-bearing function is called a blind arch .
The shape and width are chosen so that no tensile forces occur in the arch . The arch covers the so-called support line . The forces to be applied in the fighters at its ends are inclined to the vertical, i. This means that there is not only vertical pressure but also horizontal thrust.
The vault is the archetype of the arch. Arches added later are made of wood, iron or concrete. The extension of an arch into the third dimension is the dome .
Arches are not self-supporting until they are completed and require falsework .
So-called false arches or cantilever arches consist of extensions of straight beams successively further to the center. They can be created without falsework.
The arch can be found in architecture on numerous buildings in different designs. The arch enables door and window openings as well as spanning halls. In construction it is used in bridges and tunnel ceilings.
Arch types
bar
A beam that closes an opening ( window , door , gate ) in the brickwork at the top is subjected to bending loads: the top is compressed, the bottom is stretched. While wood can absorb high tensile stresses, the tensile strength of stone, especially masonry, is very low. Stone beams can only bridge small openings. They were therefore often relieved by an additional arch built over them (often invisible under the plaster).
Overlay arch
If the wall arch provided for relief, described above, is visibly used to structure the facade or wall, it is called an overlay arch. In historicism, it can also consist of sandstone or even just be dressed up, sometimes it is decorated with a keystone. Small, statically ineffective arches (usually decorated in the shape of rods) that are blinded over a wall opening are sometimes referred to as overlapping arches.
Cantilever arch
Shield arch
Real bow
Loose masonry has no tensile strength at all. Mortar doesn't change that much either. Its task is to improve the support of the stones, but not to glue the stones together. In contrast, the compressive strength is extremely high. With cement it is approx. 50 MN / m², approx. 10 times higher than the tensile strength.
Beams and cantilever arches require materials that can withstand tension. Only an arch construction uses the high compressive strength of mineral (stone and concrete) and ceramic (brick) building materials.
The stones in the two pictures on the left are bevelled in a wedge shape and can be joined together to form an arch. Only the two “posts” are secured against moving sideways. The arch stones themselves are not glued and therefore cannot absorb any tensile forces. The stones lying loosely against one another in this way are nevertheless able to absorb high loads as compressive stresses which - in contrast to a cantilever arch - are a multiple of their own weight.
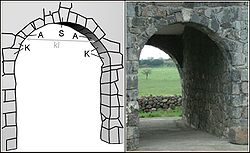
The beveled arch stones are called wedge stones . The middle stone in the arch is called the keystone ( S , see picture on the right) and is often carved out decorative.
The fighter ( K ) is both the upper end of the abutment and the base of the arch. This transition area must be worked carefully so that the pressure forces of the arch can be dissipated. The stones above the fighting line ( kl ) no longer rest on the abutment due to their own weight when the arch is erected. You need the construction by a falsework be supported so as not to fall. The actual arch begins above the fighter line.
The first stones that rest on the fighter are called beginners ( A ). The arch reveal is the inner surface of the arch (shaded dark gray in the illustration), the front is the arch front . The upper surface of the arch, the arch back , carries the stones piled upwards. The highest point of the arch reveal is called the arch apex . A stilted arch stands with its ends on more or less high or more vertical beginners, which are also known as arched stilts . As a rule, arched stilts are arranged symmetrically. Unbalanced or one -hip stilts are rather rare .
An arc that opens downwards and absorbs the forces evenly as compressive stress can be viewed as the reversal of a freely hanging chain in which only tensile forces prevail. The ideal line of an unloaded bow is therefore a catenoid . Nevertheless, a semicircular arch of a bridge comes very close to the ideal structure, since the arch has to carry more mass than the middle at the beginning and end because of the bridge ramp.
While the ancient Greek stone monumental buildings were traditionally based on wooden structures, the Romans consistently used semicircular arches as load-bearing structures (see below).
Arch constructions
Various types of bows have been developed over the centuries, with respective advantages and disadvantages.
Cantilever arch

The picture shows a typical Mayan arch. Since real arches were unknown, only small widths could be spanned; the stability was achieved by side loads.
More examples under cantilever arches and cantilever vaults .
Gable arch
The gable arch , also known as a triangular arch (French: Arc en miter ), is an arch construction made of two inclined, gable-shaped stones placed next to one another. In this respect, it is formed by two straight lines, but structurally fulfills the requirements of an arc.
Semicircular arch or round arch
In the case of a circular arc , also known as a round arch , the arc line is circular and takes up the complete semicircle (180 degrees), which means that the two lowest joints are horizontal. The height of the arch (crown height) is always exactly half the span. The semicircle has long been the dominant technique of bow making. It was perfected by the Romans and used in a variety of ways, which continued into the Romanesque period .
Pointed arch

The pointed arch is an arch constructed from two circles with a point. It is considered a central element of Gothic architecture in architecture .
The first pointed arches were found in the Burgundian Romanesque. In Gothic sacred architecture ( Saint-Denis Basilica ) they were used from the first half of the 12th century. This arch form spread from France to Germany around 1200, was used until the early 16th century and was taken up again centuries later in the neo-Gothic era.
Types: normal pointed arch, pressed pointed arch, raised pointed arch or lancet arch.
Tudor Arch
In architecture, a Tudor arch is a very flat pointed arch that is characteristic of the Tudor style . It was particularly popular in England , which is why it is also called the English pointed arch or the Norman arch . It consists of four circular arcs, each with two different sized radii.
See also: House of Tudor
Segment arch
A segment arc (flat arc, stitch arc, circular partial arc, partial circular arc) is an arc that does not describe a full semicircle, but a segment of a circle with an angle of less than 180 °. The segment arc is thus flatter than a semicircular arc. The disadvantage, however, is the greater sideshift exerted by the segment arch. The flat construction with segmented arches is particularly advantageous for wide-span arched bridges where the sideshift is introduced into the adjacent soil and which can therefore be built much flatter than bridges with semicircular arches.
Basket bow
The basket bow (also: pressed bow, basket handle bow, advice bow) combines properties of the semicircular bow and the segment bow; as with the former, the verticals merge seamlessly into the arch. The height requirement is reduced by the fact that the radius of curvature increases from the fighters to the vertex, the curvature from the vertex to the abutments. Usually, such arcs were constructed from segments with specific radii and centers, but the radius can also continuously increase and decrease again. Arcs with three or five centers are the norm.
A special form of the basket arc is the einhüftige ellipsoidal , also gooseneck , increasing sheet , falling sheet , aspiring sheet , curved sheet , Hornbogen , clamping bow or hip curve called, in which the fighter points are at different heights. This type of arch is often found in the struts of Gothic churches. The single-hip basket arch is also used for the load-bearing substructure of stairs.
Straight bow

A straight arch , also called a horizontal arch , is an arch that is designed in such a way that the underside of the spanned opening resembles a lintel. Constructively, it is a segmented arch, the wedge stones of which are worked in such a way that a horizontal lower edge results. Straight arches do not allow large spans. They are often found above windows and doors. Log arches also serve as relief arches over a lintel made of stone . Today you can find many fake, straight arches on new buildings, which are not load-bearing arch structures, but are anchored in reinforced concrete columns behind. They are often easy to recognize because the stones are not arranged radially or because the central keystone has no sloping side edges or was even installed the wrong way round.
Log arches are used in furnace construction to slightly minimize the size of the openings.
Horseshoe arch
Horseshoe arches get their name from the horseshoe-like shape. The arc length is between 2/3 and 3/4 of a circumference. This arch is predominant in Islamic architecture and is therefore also called a Moorish arch or Arabic arch . However, the Visigoths were already using the horseshoe arch in their church buildings (earliest example: San Juan de Baños , consecrated in 661, before Islam found its way into the Iberian Peninsula).
Another trail leads to India , where the Buddhist Chaitya windows of the time around the birth of Christ and later the kudus and chandrasalas derived from them are designed in the shape of a horseshoe (see also the keyhole windows of Nachna ).
Curtain arch
The curtain arch is an arch bounded by two or more convex arch lines.
Serrated arch
The zig-zag arch or multi-pass arch is an arch shape whose soffit consists of passes and noses. The simplest form of a pointed arch is the clover leaf arch or three-pass arch . The cloverleaf arch is made up of three arcs, whereby the middle arc can be larger. There are also pointed trefoil arches where the middle arch is a pointed arch. If a serpentine arch consists of more than three arches, this is the actual serpentine arch, which is also called a multi-pass arch or fan arch .
- see also Nonnenkopf
Catenoids

The catenoid ( chain line , chain curve, rope curve) is the mathematical ideal model of an arch with even mass distribution and without additional force. Free-standing arches of this shape can be made very slim. An example, but with an uneven mass distribution, is the Gateway Arch in St. Louis.
Parabolic arch

Due to the small deviation from a catenoid, arcs are sometimes designed as a parabola . When the arch carries a load, as in the example image on the left, the ideal line flattens out. It is neither a catenoid nor a parabola, but rather approaches a semicircle.
Elliptical arch

Shapes: standing, rising, raised elliptical arch. The curve follows the ellipse. Both focal points lie on the fighting line.
Carnies arch
At the carnation arch , two corbels with a convex curved profile are attached above the spur line , to which the concave curved arch connects, so that an S-shaped line is created in the connection of the two elements. Carnies generally refers to an S-shaped, i.e. concavo-convex profiled component.
Keel bow
A bow whose edge looks like the profile of a keeled ship on its back is called a keel bow . Other names for it are donkey back - derived from the back shape of a donkey - and saddle bow , Scottish bow or accolade .
Shoulder arch

The shoulder arch is actually a straight arch, the lintel support width of which has been shortened by underlying corbels or console stones. Other names are therefore bracket arch and cantilever arch .
Schwibbogen
The Schwibbogen or Schwiebbogen is an arch that straddles two buildings. The arch is so walled over that there is a straight finish at the top. The Schwibbogen can often be found in the narrow streets of medieval cities, e.g. B. Regensburgs .
Buttresses
The buttress is an asymmetrical arch that supports towering components. It is a typical construction feature of Gothic basilicas as part of the buttress .
Use of bow

- Bridge arch : the load-bearing element of astone bridge , is a borderline case to a barrel vault.
- Choir arch : arch between choir and nave or between choir and crossing . This arch is also called the triumphal arch.
- Relief arch: an arch that lies completely in the masonry in order to relieve the underlying parts and to distribute the forces to other areas. Often built over stone lintels . The remaining space between the lintel and the relief arch is only loosely walled up.
- Stilted arch : can often be found in Romanesque choir apses , in the arcades surrounding the choir that open into the ambulatory .
- Belt arch : supports barrel vaults or separates individual fields of a cross vault and connects the supporting pillars .
- Wall arch : spans an opening in the masonry as a window or archway and carries the weight of the masonry above.
- The Triumphal Arch : is a monumental monument erected in the form of a free-standing arch. The choir arch is also called the triumphal arch.
Construction details
The following geometric constructions are used for arches in practice:
- Round arch
- Halving the combatant line AB results in point M, the starting point for drawing the round arch with R = distance AM or BM.

- Segment arch, flat arch, stitch arch
- Arc axis AB and random height C. are placed perpendicular bisector of the segment AC build; Intersection point in M arises. Point M is the center of the circle sought. Draw a circle with the radius r = MC around M. The arc between the combat points A and B is the segment arc you are looking for.
- Gothic arch
- With the span around point A and around point B, create an arc with radius R = AB, results in vertex S. The connection of points A, B, S results in an equilateral triangle.
- Gothic arch, pressed
- Erect the vertical center line on the fighting line AB. Then subtract the stitch height of the arch and you get the vertex S. The stitch height must be significantly smaller than the span, but larger than half the span. The vertical line on the line BS intersects the fighter line and results in the starting point M1 for drawing the arc with R1. By transferring you get the starting point M2 on the other side.
- Gothic arch, elevated
- (Construction A) In this construction, the puncture points are outside the transom points and the span. The fighting line is divided into four equal parts. The distance of 1/4 is plotted to the right and left of the fighter points and form the entry points M1 and M2.
- Basket arch from three centers
- For the span S = AB, one first draws the vertical center line and plots the stitch height H = MC on this. Then you connect the points A and C, remove the stitch height MC from M on the segment AM and get point D and thus the segment AD = L. From C you remove L on the segment AC and get the arc centers M1 and M2. From M, the route MM1 is removed from the route MB and M3 is obtained. The arcs around the centers of the arcs M1, M2 and M3 result in the basket arc.
- Basket arch from five centers
- First, draw the vertical center line for the span S = AB, add the stitch height H = MC to this and mark an angle of 45 ° at the center line at point C, and get the distance DE = L. From M, move to the right and left on the route AB, the route L and gets the arc centers M1 and M2. Then, on the mid-vertical from M, the distance L is plotted downwards twice and the point F and the arc center M3 are obtained. From point F lines are drawn through the arc center points M1 and M2, add to the center perpendicular at point M to the left and right below at an angle of 45 ° (approximation angle - not mathematically exact!) And obtain the arc centers M4 and M5. Lines from the arc center M3 through the arc centers M4 and M5 delimit the central arc section. The arcs around the centers of the arcs M1 - M5 result in the basket arch. The mathematically exact angle is 41.53 ° with the formula: .
- Basket arch from eleven centers
- If there are more than three centers, the shape of the ellipse can be approximated by drawing the auxiliary circles II, II II and III III with half the span AO, the arrow height OC and the sum of both. If one then divides one of these auxiliary circles into an even number n + 1 equal parts, if n means the number of the desired center points, then draws the radius O a2, O b2 etc., determined by drawing the parallels a a ', b b', etc. major axis or to the minor axis a1 a ', b1 b', etc. the ellipse points a ', b', c ', etc., the intersection of the connecting line a2 a' with AO results in the center M11 for the first circle segment A a '. The connecting line b2 b 'intersects the extension of the preceding radius at the center M10, etc. However, this embodiment, as well as the other various graphic constructions, result in very grinding cuts for determining the center points, and it is better to determine the radius themselves or the coordinates of the center points by setting up a corresponding equation to calculate.
- Single-hip basket arch, gooseneck, rising arch or hip arch
- (Construction A) With a given slope EB, a perpendicular is erected in the center O of the span AE. Distance AD = DC. Then a vertical line is made from C to AB. The result is the intersection points M1 and M2 with AE or with the horizontal through B. The two sought-after center points for the circular arcs are found.
- Tudor Arch
- (Construction A) The distance AB and the center perpendicular are given. Make a semicircle around M with the radius AM down. Divide the segment AB into four equal parts. Point 1 and point 2 are created. Turn 1, with the radius of the line between 1 and 2, an arc downwards that intersects the arc with the radius AM. The point of intersection is point 3. The same construction steps are repeated for point 2, resulting in point 4. Now draw rays from point 1 through point 3, and from point 2 through point 4, to subdivide the various arcs. Points 1, 2, 3, and 4 are the puncture points for the Tudor arch.
- Carnies arch
- For a given stitch height C, points A and C are connected to one another. Line AC is divided into four equal sections a. Plumb lines are drawn on the line AC upwards to the vertical A-axis and downwards to the vertical C-axis. The arc points M1 and M2 are thus obtained. The arcs are connected to each other and mirrored to B.
- Parabolic arch
- Parabolic arch construction using tangents. The span S and the arch height MC are known. The distance L = 1/1 is divided into four equal parts (L = 1/4). Lines aa, bb and cc are now formed; the tangent points T1, T2, T3 for drawing a parabola are created.
- Horseshoe arch
- Horseshoe arch. It consists of a round arch, the center of which lies above the level of the fighter; it can be constructed with half the span as a radius. The horseshoe arch is constructed with a slope of 30 ° from the fighter points A and B. The horseshoe pointed arch is constructed with a bevel of 45 ° from the fighter points A and B.
- Keel bow
- Keel bow (construction A). The distance AB and the middle perpendicular are given. In this construction, the segment AB is divided into four equal parts (a). The points M1 and M2 are created. Make a semicircle around M1 and M2. Vertical lines from point M1 and M2 are drawn upwards. From the respective vertices of the semicircles around M1 and M2, the distance a is plotted vertically upwards - the points M3 and M4 are now created. The quarter circles are drawn around points M3 and M4. The result is the vertex C.
literature
- Oscar Mothes: Illustrierter Bau-Lexikon Volume 3 , Leipzig, Spamer, 1868, 562 S. Online version , accessed on May 4, 2017.
- Glossarium Artis . Vol. 3. Arches and Arcades / Tübingen 1973; Rudolf E. Huber, Renate Rieth, Courvoisier, Jean; KG Saur Verlag KG, ISBN 3-598-10454-5
- The stone structures . Franz Stade, Reprint-Verlag-Leipzig; Reprint edition of the original edition from 1907; Volker Hennig, Holzminden; ISBN 3-8262-1922-8
- Building expertise building construction. Author Kohl, Bastian, Neizel. Teubner Stuttgart, Leipzig 1998. ISBN 978-3-322-83011-1 , e- ISBN 978-3-322-83010-4 .
- Karl-Eugen Kurrer : History of Structural Analysis. In Search of Balance , Ernst and Son, Berlin 2016, pp. 198-273, ISBN 978-3-433-03134-6 .
Web links
Individual evidence
- ^ Meyers Großes Konversations-Lexikon, 6th edition 1905–1909: Definition sheet. Retrieved February 8, 2017 .
- ↑ Cover sheet dictionary
- ^ Paragraph based on Hans Koepf , Günther Binding : Picture Dictionary of Architecture (= Kröner's pocket edition. Vol. 194). 4th, revised edition. Kröner, Stuttgart 2005, ISBN 3-520-19404-X . The synonymy to triangular arches is no longer found in the 4th edition, but in the older 2nd edition, ISBN 3-520-19402-3 . In a different meaning, gable arch is also understood to mean an ornament, as in Günther Wasmuth (ed.): Wasmuths Lexikon der Baukunst. Volume 3: H to Ozo. Wasmuth, Berlin 1931, cf. Gable # gable decoration
- ↑ pointed arch. Retrieved July 19, 2020 .
- ↑ Tudor Arch. Retrieved February 8, 2017 .
- ^ A b Wilhelm Friedrich: Book of tables for the building and wood industry. Edition B. Fachbuchverlag GmbH., Leipzig 1951.
- ↑ Hans Koepf, Günther Binding: Picture Dictionary of Architecture (= Kröner's pocket edition. Vol. 194). Kröner, Stuttgart 1999, ISBN 3-520-19403-1 .
- ^ Wilfried Koch : Architectural Style. The standard work on European architecture from antiquity to the present. 29th, revised edition. Wissenmedia, Gütersloh et al. 2009, ISBN 978-3-577-10231-5 , p. 458.
- ↑ Schwibbogen. Retrieved May 4, 2017 .
- ↑ Harald Lotter and Alexander Wendel: Bogenarten. (No longer available online.) Archived from the original on November 28, 2004 ; Retrieved December 9, 2013 . Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ^ Basic knowledge of construction , authors: Batran, Frey, Hühn, Köhler, Kraus, Rothacher, Sonntag, publisher: Handwerk und Technik GmbH, Hamburg 1985, ISBN 3-582-03500-X
- ↑ Calculation formulas for basket arches. Retrieved April 23, 2020 .
- ↑ Architectural drawings , authors: Dahmlos and Witte, 6th edition, publisher: Gebrüder Jänecke, Hanover 1972, ISBN 3-7792-1032-0
- ↑ Calculation formulas for basket arches. Retrieved April 23, 2020 .
- ↑ basket arch. Retrieved June 7, 2020 .
- ↑ Calculation formulas for basket arches. Retrieved June 7, 2020 .
- ↑ The constructions in stone. Author GA Breymann. JM Gebhardt's Verlag Leipzig, 1903, ISBN 3-88746-013-8 .
- ↑ One-hip basket arch construction. Retrieved February 14, 2017 .
- ↑ Calculation formulas for basket arches. Retrieved April 23, 2020 .
- ↑ Meyers Großes Konversations-Lexikon , 6th edition 1905-1909: Tudorbogen. Retrieved February 8, 2017 .
- ↑ Lexicon of all technology , edited by Otto Lueger, 2nd edition 1904–1920: Tudorbogen. Retrieved February 8, 2017 .
- ↑ Keel arch / donkey back / curved pointed arch. Retrieved November 3, 2017 .