Cyrillic number font

If characters are not displayed correctly in the following, this is due to the font, see Representation of Cyrillic Numbers in Unicode and Help with Display Problems .

҂ви҃і

(2018 as a cyrillic number)

The Cyrillic number font is based on the Cyrillic letters . It is used by the South and East Slavs in mainly Church Slavonic texts, which are written in old Cyrilliza . Indian and Roman numerals have also been used since the 16th century . In the bourgeois script introduced by Peter I in 1708 , Cyrillic numerals are no longer used.

Numerical values ​​of the Cyrillic letters

The number system used in Cyrillic is an addition system in which a total of 27 letters for the numbers up to nine (1, 2, ... 9), the multiples of ten (10, 20, ... 90) and the multiples of one hundred (100, 200, ... 900).

This system is based directly on the Milesian type of the Greek numerals . Therefore, all Cyrillic letters have the numerical value of the corresponding Greek letters . The letters Stigma / Digamma , Koppa and Sampi , which were already obsolete in Greek and were only used there as numerals, were replaced by Cyrillic letters that did not go back to the Greek and looked similar to them externally. All other specifically Slavic letters ( б , ж , ш , щ etc.) have no numerical value.

In order to indicate that the letters should not be interpreted as phonetic values ​​but as numbers, a titlo is placed over the number representation (sometimes over each individual number symbol). (In Greek this function is followed by an apostrophe after the representation.) The representation of a number is also often enclosed in dots.

value Greek Cyrillic 1 αʹ а҃ 2 βʹ в҃ 3 γʹ г҃ 4th δʹ д҃ 5 εʹ е҃ 6th ϛʹ or ϝʹ ѕ҃ 7th ζʹ з҃ 8th ηʹ и҃ 9 θʹ ѳ҃

value Greek Cyrillic 10 ιʹ і҃ 20th κʹ к҃ 30th λʹ л҃ 40 μʹ м҃ 50 νʹ н҃ 60 ξʹ ѯ҃ 70 οʹ о҃ 80 πʹ п҃ 90 ϟʹ ч҃

value Greek Cyrillic 100 ρʹ р҃ 200 σʹ с҃ 300 τʹ т҃ 400 υʹ ѵ҃ 500 φʹ ф҃ 600 χʹ х҃ 700 ψʹ ѱ҃ 800 ωʹ ѡ҃ 900 Ϡʹ ц҃ or ѧ҃

A comparison of the partially different Cyrillic and Glagolitic numerical values ​​of the letters can be found in the article " Glagolitic numerals ".

Combination of numerals

Numbers that are greater than 10 and not divisible by 10 are written by combining the number signs to a sum, for example 23 = 20 + 3 (Cyrillic кг҃) or 735 = 700 + 30 + 5 (ѱл҃е ·). "Zeros" are left out (similar to the Roman numerals ), for example 705 = 700 + 5 (· ѱе҃ ·).

The characters are usually written from left to right in descending size. A special feature, however, is that the numbers from 11 to 19 are written "backwards" according to the sequence when speaking, i.e. 113 = 100 + 3 + 10 (· рг҃і ·) according to the pronunciation as sъto tri na desęti 'one hundred three to ten' (cf. German one hundred-three-ten ). In contrast to German, the numbers from 21 onwards are spoken and written in the “logical” order, for example 123: sъto dъvě desęti tri 'one hundred two-ten three' (cf. English a hundred and twenty-three ), i.e. 100 + 20 + 3 (рк҃г).

Numbers from 1000

Since there are no numerals for thousands, the highest number that can be represented with this system is 999 (900 + 90 + 9, · цч҃ѳ ·). For numbers from 1000, a thousand character (҂) is therefore written in front of a letter, which indicates that the numerical value of the following letter must be multiplied by 1000, i.e. ҂а = 1000, ҂в = 2000, etc. (In Greek there is a type Comma in front of the number, i.e. ͵α, ͵β etc.)

Examples:

• = ҂аѱ҃ѕ = 1706
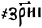• = · ҂зри҃і · = 7118 (corresponds to the year 1610 AD as the year since creation after the Byzantine era )

In this way, higher numbers can also be represented, for example · ҂к҃ · = 20,000 or · ҂ц҂ч҂ѳ҃цчѳ · = 999 999. In addition, there are other ways of representing powers of ten:

See also

• Cyrillic alphabet

Individual evidence

1. ↑ S. a. TITUS DIDACTICA: The history of the development of Slavic alphabets
2. ↑ See Вячеслав Николаевич Щепкин: Русская палеография. 3rd, supplemented edition. Аспект Пресс, Москва 1999, ISBN 5-7567-0233-4 , p. 165.