Magneto-optic Kerr effect

The magneto-optical Kerr effect ( MOKE ) from magneto-optics describes a change in the intensity or a rotation of the plane of polarization of light that is reflected on ferromagnetic metal surfaces . The change in intensity or the angle of rotation depends on the geometry and the magnetization of the sample.

The magneto-optic Kerr effect should not be confused with the electro-optic Kerr effect , in which electric fields rotate the plane of polarization of polarized light. The magneto-optic Kerr effect was discovered by John Kerr in 1876 .

General

The magneto-optical Kerr effect (MOKE for short) describes a rotation of the plane of polarization of a linearly polarized light beam by an angle when it is reflected on a solid surface with magnetization . Such magnetization exists in ferromagnets or paramagnets located in a magnetic field . The change in the plane of polarization is proportional to the magnetization of the sample. The magnetization of the sample can thus be described via this Kerr angle and the change in the same in the external magnetic field can be observed. A similar effect also occurs when light is transmitted through the sample. This is called the Faraday effect . Both effects result directly from off-diagonal elements of the permittivity tensor . ${\displaystyle \theta _{\mathrm {K} }}$ ${\displaystyle {\vec {M}}}$ ${\displaystyle \theta _{\mathrm {K} }}$

In addition to the MOKE, which is linearly dependent on the incident light intensity, there is also a nonlinear magneto-optical Kerr effect (NOLIMOKE) at high light intensities in the area of non-linear optics .

application

The MOKE is the basis for magneto-optical Kerr spectroscopy and magneto-optical data storage .

If the polarization rotation is converted into a change in brightness by an analyzer (polarizer), the MOKE can be used to visualize stray magnetic fields .

Geometries

The magneto-optical Kerr effect occurs in different forms, which are defined by the position of the magnetization in relation to the plane of incidence of the light.

Polar magneto-optic Kerr effect

With the polar magneto-optical Kerr effect (PMOKE), the direction of magnetization is perpendicular to the surface. In the reflected beam, it causes a rotation of the plane of polarization and a change in polarization from linearly polarized to elliptically polarized. This type of MOKE is used in magneto-optical data carriers , since the effect is greatest in this geometry and thus the achievable data density is maximum.

Longitudinal magneto-optical Kerr effect

In the longitudinal magneto-optical Kerr effect (LMOKE), the direction of magnetization is parallel to the surface and in the plane of incidence of the light. Like the PMOKE, it causes a rotation of the plane of polarization of the reflected beam. This effect is typically an order of magnitude smaller than PMOKE.

Transverse magneto-optic Kerr effect

In the transverse magneto-optical Kerr effect (TMOKE), the direction of magnetization is parallel to the surface and perpendicular to the plane of incidence of the light. This effect only occurs when the incident light is polarized in the plane of incidence (p-polarization). It causes a change in the intensity of the reflected beam and not a rotation of the plane of polarization like the PMOKE and the LMOKE. The TMOKE is typically an order of magnitude smaller than the LMOKE.

Square magneto-optic Kerr effect

In the square magneto-optical Kerr effect (QMOKE), also known as the Voigt effect , the change in the polarization of the reflected light depends on product terms of the polar, longitudinal and transverse magnetization components. QMOKE can be of the same order of magnitude as LMOKE and is anisotropic in single-crystalline materials. that is, the effect depends on the orientation of the crystal axes relative to the plane of incidence.

Kerr angle at the PMOKE

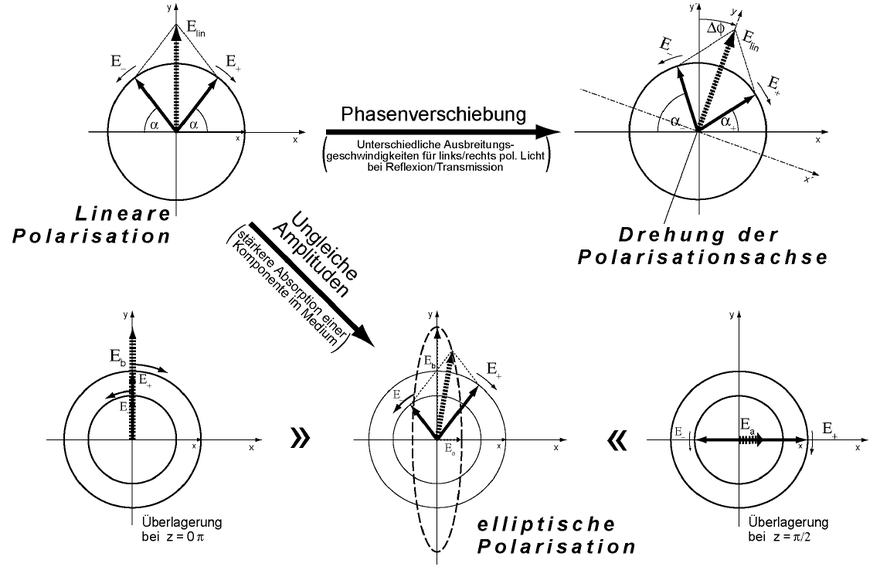
If a linearly polarized wave reflects on a magnetized surface, the plane of polarization rotates by the Kerr angle in relation to its initial direction . In addition, the linearly polarized wave is elliptically polarized. ${\displaystyle \theta _{\mathrm {K} }}$

The rotation is due to the fact that the material has different refractive indices for the different circulating waves after it has been magnetized, which results in different phase velocities . This results in a phase difference between the two waves and thus a change in the polarization axis by the Kerr angle. The material also has different absorption coefficients for right and left circularly polarized light, which means that the intensities change. This explains the ellipticity. This phenomenon is called magnetic circular dichroism .

Both pieces of information are given in the complex Kerr angle : ${\displaystyle \Phi _{\mathrm {K} }}$

${\displaystyle \Phi _{\mathrm {K} }=\Theta _{\mathrm {K} }+i\eta }$

${\displaystyle \eta }$indicates the ellipticity for which applies where and are the amplitudes of the waves. Since the intensity of a wave is directly proportional to its amplitude square, it follows ${\displaystyle \eta =\arctan(b/a)}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle I}$

${\displaystyle \eta =\arctan \left({\sqrt {I_{\mathrm {r} }/I_{\mathrm {l} }}}\right)}$

with the intensities for the right-circularly polarized and for the left-circularly polarized component. ${\displaystyle I_{\mathrm {r} }}$ ${\displaystyle I_{\mathrm {l} }}$

literature

• ZQ Qiu, SD Bader: Surface magneto-optic Kerr effect . In: Review of Scientific Instruments . tape 71 , no. 3 , 2000, pp. 1243-1255 , doi : 10.1063 / 1.1150496 .
• M. Grimsditch, P. Vavassori: The diffracted magneto-optic Kerr effect: what does it tell you? In: Journal of Physics: Condensed Matter . tape 16 , no. 9 , 2004, p. R275 – R294 , doi : 10.1088 / 0953-8984 / 16/9 / R01 .

See also

• Kerr magnetometer

Individual evidence

1. ↑ MagView - Magneto-optical visualization of magnetic fields ; Web presence of Matesy GmbH.