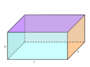
Prismatoid

A prismatoid is a geometric body. It is a polyhedron with parallel polygons as the base and top surface as well as triangles , trapezoids or parallelograms as side surfaces. In contrast to the prism , the base and top surface do not have to be congruent or have the same number of corners. A prismatoid in which the base and top surfaces are polygons with the same number of corners and whose side surfaces consist only of trapezoids and parallelograms is also known as a prismoid .

The volume of a prismatoid can be calculated according to the formula ${\ displaystyle V}$

{\ displaystyle V = {\ frac {h} {6}} (A_ {G} + 4A_ {S} + A_ {D})}

to calculate. Here are the base area, the area at medium height, the roof area and the height. ${\ displaystyle A_ {G}}$ ${\ displaystyle A_ {S}}$ ${\ displaystyle A_ {D}}$ ${\ displaystyle h}$

This is one of the most famous and universal volume formulas. In honor of its discoverer Johannes Kepler , it is called Kepler's barrel rule .

The prismatoids include:

The scutoid is not a prismatoid in the true sense of the definition , as it is not a polyhedron due to its curved boundary surfaces.

literature

Amos Day Bradley: Prismatoid, Prismoid, Generalized Prismoid. In: The American Mathematical Monthly. Volume 86, No. 6, June / July 1979, pp. 486-490, JSTOR 2320427 .
Bruce E. Meserve, Robert E. Pingry: Some Notes on the Prismoidal Formula. In: The Mathematics Teacher. Volume 45, No. 4, April 1952, pp. 257-263, JSTOR 27954012 .
Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey. Solid Geometry in the 21st Century (= The Dolciani Mathematical Expositions. 50). The Mathematical Association of America, Washington DC 2015, ISBN 978-0-88385-358-0 , pp. 85-89 .

Web links

Eric W. Weisstein : Prismatoid . In: MathWorld (English).

Individual evidence

^ Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey. Solid Geometry in the 21st Century (= The Dolciani Mathematical Expositions. 50). The Mathematical Association of America, Washington DC 2015, ISBN 978-0-88385-358-0 , pp. 85-89 .
↑ Note: In the German literature there is occasionally no distinction between prismatoid and prismoid and the terms are instead used synonymously, e.g. B. at Nitschke.
↑ ^a ^b Martin Nitschke: Geometry. Application-related basics and examples for engineers. 2nd updated edition. Fachbuchverlag Leipzig in Carl-Hanser-Verlag, Munich 2014, ISBN 978-3-446-44143-9 , pp. 50-51 .

[Alsina-1] Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey. Solid Geometry in the 21st Century (= The Dolciani Mathematical Expositions. 50). The Mathematical Association of America, Washington DC 2015, ISBN 978-0-88385-358-0 , pp. 85-89 .

[2] Note: In the German literature there is occasionally no distinction between prismatoid and prismoid and the terms are instead used synonymously, e.g. B. at Nitschke.

[Nitschke-3] Martin Nitschke: Geometry. Application-related basics and examples for engineers. 2nd updated edition. Fachbuchverlag Leipzig in Carl-Hanser-Verlag, Munich 2014, ISBN 978-3-446-44143-9 , pp. 50-51 .