SL (2, R)

This article deals with the special linear group , for the Lie algebra see sl (2, R) . ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle {\mathfrak {sl}}(2,\mathbb {R} )}$

The special linear group or is the group of real - matrices with determinant 1: ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle \operatorname {SL} _{2}(\mathbb {R} )}$ ${\displaystyle 2\times 2}$

${\displaystyle {\mbox{SL}}(2,\mathbb {R} )=\left\{\left({\begin{matrix}a&b\\c&d\end{matrix}}\right):a,b,c,d\in \mathbb {R} {\mbox{ und }}ad-bc=1\right\}.}$

It is a Lie group with diverse applications in geometry , topology , representation theory , harmonic analysis , number theory , modular forms and physics .

Representation theory

For every natural number there is a -dimensional, irreducible representation of the, which is unambiguous except for isomorphism . An explicit realization of this irreducible representation is as follows. Be ${\displaystyle d}$ ${\displaystyle (d+1)}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$

${\displaystyle V_{d}=\left\{f(x,y)=a_{0}x^{d}+a_{1}x^{d-1}y+a_{2}x^{d-2}y^{2}+\ldots +a_{d-1}xy^{d-1}+a_{d}y^{d}:a_{0},\ldots ,a_{d}\in \mathbb {R} \right\}}$

the vector space of the homogeneous polynomials of degree in 2 variables. This vector space is -dimensional and works through ${\displaystyle d}$ ${\displaystyle (d+1)}$ ${\displaystyle A\in \operatorname {SL} (2,\mathbb {R} )}$

${\displaystyle (Af)(x,y):=f(A^{-1}(x,y)).}$

The Veronese embedding is equivariant with respect to the irreducible representation . ${\displaystyle \nu _{d}\colon \mathbb {R} P^{1}\to \mathbb {R} P^{d}}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )\to \operatorname {SL} (d+1,\mathbb {R} )}$

The infinite-dimensional representations of the are described by the Langlands classification . ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$

Lie algebra

→ Main article : sl (2, R)

${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$is a Lie group , its Lie algebra is the Lie algebra of the traceless matrices ${\displaystyle 2\times 2}$

${\displaystyle {\mathfrak {sl}}(2,\mathbb {R} )=\left\{A\in \operatorname {Mat} (2,\mathbb {R} ):\operatorname {Sp} (A)=0\right\}}$.

A vector space basis of the 3-dimensional vector space is for example ${\displaystyle {\mathfrak {sl}}(2,\mathbb {R} )}$

${\displaystyle H=\left({\begin{array}{cc}1&0\\0&-1\end{array}}\right),\ X=\left({\begin{array}{cc}0&1\\0&0\end{array}}\right),\ Y=\left({\begin{array}{cc}0&0\\1&0\end{array}}\right)}$

with the commutator relations

${\displaystyle \left[H,X\right]=2X,\ \left[H,Y\right]=-2Y,\ \left[X,Y\right]=H}$.

This Lie algebra is simple , it has two non-conjugated Cartan subalgebras : one generated by , the other generated by . ${\displaystyle H}$ ${\displaystyle X-Y}$

The killing form is . It is negative definite on the subspace generated by, positive definite on the subspace generated by and . ${\displaystyle B(V,W)=4\operatorname {Sp} (VW)}$ ${\displaystyle X-Y}$ ${\displaystyle H}$ ${\displaystyle X+Y}$

Linear Algebra

Matrices from corresponding invertible linear mappings of the vector space . The matrix works through ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \left({\begin{matrix}a&b\\c&d\end{matrix}}\right)}$

${\displaystyle \left({\begin{matrix}a&b\\c&d\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)=\left({\begin{matrix}ax+by\\cx+dy\end{matrix}}\right).}$

Matrices from preserve the volume shape, but generally not the Euclidean metric of the . ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle \mathbb {R} ^{2}}$

Classification of the 2 × 2 matrices

The eigenvalues ​​of a matrix are zeros of the characteristic polynomial ${\displaystyle A\in \operatorname {SL} (2,\mathbb {R} )}$

${\displaystyle \lambda ^{2}-\mathrm {Sp} (A)\lambda +1=0}$

and can be calculated using the formula for solving quadratic equations as

${\displaystyle \lambda ={\frac {\mathrm {Sp} (A)\pm {\sqrt {\mathrm {Sp} (A)^{2}-4}}}{2}}}$.

The matrices are then classified according to the following classification:

• If so , then is an elliptical matrix. ${\displaystyle \vert \operatorname {Sp} (A)\vert <2}$ ${\displaystyle A}$
• If so , then it is a parabolic matrix. ${\displaystyle \vert \operatorname {Sp} (A)\vert =2}$ ${\displaystyle A}$
• If so , then is a hyperbolic matrix. ${\displaystyle \vert \operatorname {Sp} (A)\vert >2}$ ${\displaystyle A}$

Elliptical elements

Rotation with fixed point 0.

Elliptical elements are of the shape

${\displaystyle A\left({\begin{matrix}\cos \phi &\sin \phi \\-\sin \phi &\cos \phi \end{matrix}}\right)A^{-1}}$

with and . ${\displaystyle \phi \in \mathbb {R} /2\pi \mathbb {Z} }$ ${\displaystyle A\in \operatorname {SL} (2,\mathbb {R} )}$

The matrix acts on the Euclidean plane as a rotation with fixed point 0 and rotation angle . ${\displaystyle \left({\begin{matrix}\cos \phi &\sin \phi \\-\sin \phi &\cos \phi \end{matrix}}\right)}$ ${\displaystyle \phi }$

Parabolic elements

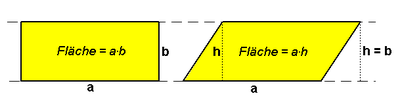
A shear maps a rectangle onto a parallelogram.

Parabolic elements are of the shape

${\displaystyle \pm A\left({\begin{matrix}1&n\\0&1\end{matrix}}\right)A^{-1}}$

with and . ${\displaystyle n\in \mathbb {R} }$ ${\displaystyle A\in \operatorname {SL} (2,\mathbb {R} )}$

The matrix acts as a shear on the Euclidean plane . ${\displaystyle \left({\begin{matrix}1&\ n\\0&1\end{matrix}}\right)}$

Hyperbolic elements

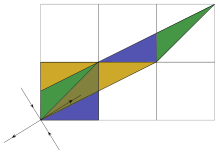
The image parallelogram has the same area as the original square.

Hyperbolic elements are of the form

${\displaystyle A\left({\begin{matrix}a&0\\0&{\frac {1}{a}}\end{matrix}}\right)A^{-1}}$

with and . ${\displaystyle a\in \mathbb {R} \setminus \left\{0\right\}}$ ${\displaystyle A\in \operatorname {SL} (2,\mathbb {R} )}$

The matrix acts as an expansion compression, i.e. That is, it expands in the direction of one eigenvector, compresses in the direction of the other eigenvector, but retains the total area. ${\displaystyle \left({\begin{matrix}a&0\\0&{\frac {1}{a}}\end{matrix}}\right)}$

Hyperbolic geometry

Matrices from act on the upper half-plane ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$

${\displaystyle \mathbb {H} =\{x+iy\ |\ y>0;\,x,y\in \mathbb {R} \}\subset \mathbb {C} }$

by

${\displaystyle z\mapsto {\frac {az+b}{cz+d}}}$.

They act as isometrics of the hyperbolic metric .

Because acts as an identity mapping, this effect of over factors ${\displaystyle \pm I_{2}}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$

${\displaystyle \operatorname {PSL} (2,\mathbb {R} )=\operatorname {SL} (2,\mathbb {R} )/\{\pm I_{2}\}}$.

Projective geometry and fractional-linear transformations

The projective straight line is the set of all straight lines through the zero point im . The effect of on gives a well-defined effect of on . ${\displaystyle \mathbb {R} P^{1}}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle \left(\mathbb {R} ^{2}\setminus \{0\}\right)}$ ${\displaystyle \operatorname {PSL} (2,\mathbb {R} )}$ ${\displaystyle \mathbb {R} P^{1}}$

A bijection between and is defined by. After this identifying and acting on a pass-linear transformations ${\displaystyle [x:y]\rightarrow {\frac {x}{y}}}$ ${\displaystyle \mathbb {R} P^{1}}$ ${\displaystyle \mathbb {R} \cup \left\{\infty \right\}}$ ${\displaystyle \mathbb {R} P^{1}}$ ${\displaystyle \mathbb {R} \cup \left\{\infty \right\}}$ ${\displaystyle \operatorname {PSL} (2,\mathbb {R} )}$ ${\displaystyle \mathbb {R} \cup \left\{\infty \right\}}$

${\displaystyle \left({\begin{matrix}a&b\\c&d\end{matrix}}\right)z={\frac {az+b}{cz+d}}}$.

The Veronese embedding is equivariant with regard to the irreducible representation . ${\displaystyle \mathbb {R} P^{1}\to \mathbb {R} P^{n}}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )\to \operatorname {SL} (n+1,\mathbb {R} )}$

${\displaystyle \mathbb {R} P^{1}=\mathbb {R} \cup \left\{\infty \right\}}$is also the edge at infinity of the hyperbolic plane . The effect of on the compactification of the hyperbolic level through fractional-linear transformations is continuous. Elliptical elements have a fixed point in , parabolic elements have one fixed point in , and hyperbolic elements have two fixed points in . ${\displaystyle \partial \mathbb {H} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle PSL(2,\mathbb {R} )}$ ${\displaystyle \mathbb {H} \cup \partial \mathbb {H} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \partial \mathbb {H} }$ ${\displaystyle \partial \mathbb {H} }$

Fuchsian groups

Discrete subgroups of are called Fuchsian groups . ${\displaystyle \operatorname {PSL} (2,\mathbb {R} )}$

The limit set of a Fuchs group is the average of with the end of an orbit , where and the definition of the limit set is independent of the selected point . ${\displaystyle \Gamma }$ ${\displaystyle \mathbb {R} P^{1}=\partial \mathbb {H} }$ ${\displaystyle \Gamma x}$ ${\displaystyle x\in \mathbb {H} }$

A Fuchs group is called a Fuchs group of the first kind if the Limes set is whole . Otherwise it is a Fuchs group of type 2. ${\displaystyle \mathbb {P} ^{1}(\mathbb {R} )=\mathbb {R} \cup \{\infty \}}$

Fuchs groups of the first kind are the so-called lattices in , i. H. discrete subgroups for which there is a fundamental domain of finite volume in the hyperbolic plane. ${\displaystyle \operatorname {PSL} (2,\mathbb {R} )}$ ${\displaystyle \Gamma }$

An example of a grid in is the modular group , which, among other things, plays a central role in the theory of modular forms with many number theoretic applications. ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle \operatorname {SL} (2,\mathbb {Z} )}$

If a Fuchs group does not contain any elements of order 2, then it is the projection of a discrete subgroup of . ( Culler's Theorem ) ${\displaystyle \Gamma \subset \operatorname {PSL} (2,\mathbb {R} )}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$

topology

The circle group is a maximally compact subgroup of . The subgroup is a deformation retract of , in particular the two spaces are homotopy equivalent . ${\displaystyle \operatorname {SO} (2)}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle \operatorname {SO} (2)}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$

The fundamental group of is isomorphic to , the higher homotopy groups are trivial. ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle \mathbb {Z} }$

The universal superposition of is an example of a Lie group which does not have a true finite-dimensional representation, i.e. is not isomorphic to any subgroup of a general linear group . ${\displaystyle {\widetilde {\operatorname {SL} (2,\mathbb {R} )}}}$ ${\displaystyle \operatorname {SL} (2,\mathbb {R} )}$ ${\displaystyle \operatorname {GL} (n,\mathbb {R} )}$

The quotient is diffeomorphic to Einheitstangentialbündel the hyperbolic plane: . ${\displaystyle \operatorname {PSL} (2,\mathbb {R} )=\operatorname {SL} (2,\mathbb {R} )/(\mathbb {Z} /2\mathbb {Z} )}$ ${\displaystyle {\operatorname {PSL} (2,\mathbb {R} )}=T^{1}\mathbb {H} }$

literature

• Serge Lang : SL ₂ (R) (= Graduate Texts in Mathematics. Vol. 105). Springer, New York NY a. a. 1985, ISBN 0-387-96198-4 .
• William P. Thurston : Three-dimensional geometry and topology (= Princeton Mathematical Series. Vol. 35). Volume 1. Edited by Silvio Levy. Princeton University Press, Princeton NJ, 1997, ISBN 0-691-08304-5 .