Spin glass

Schematic representation of the disordered spin structure of a spin glass (above) in contrast to the ordered spin structure of a ferromagnet (below)

A spin glass (including spin-glass , English spin glass ) is with respect to its spin structure and the position of the spins un -level magnetic system having a random geometric frustration . This is a quantifiable measure of the inability of the system to achieve a simple spin state of lowest energy ( ground state ) and can be expressed mathematically precisely without using the energy term.

Spin glasses (but also certain conventionally ordered systems) have an extremely large number of metastable states, which can never be passed through on experimentally accessible time scales.

Disordered frustration

A typical cause of the frustration in spin glasses is the simultaneous presence of

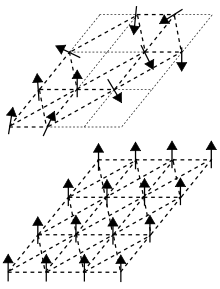
a) Interactions with a competing sign (e.g. ferromagnetic interaction between spins 1 and 2 , antiferromagnetic interaction between spins 2 and 3 , such as in the third horizontal line from the top in the adjacent sketch), and

b) Disorder , analogous to the disorder in a chemical glass (otherwise spin glasses have nothing to do with chemical glasses).

The phenomenon of "frustration" in the sense given above occurs z. B. on when an odd number of spins interact antiferromagnetically with each other. The term was taken over from high-energy physics by the French Gérard Toulouse by exploiting cross-relationships in a modified form (see quantum chromodynamics and Wilson loop , after the American Nobel Prize winner Kenneth Wilson ).

Compared to other magnetic systems

If a spin glass is brought into a (weak) external magnetic field and the magnetization is recorded as a function of the temperature , a “typical” magnetic disordered behavior is observed above the transition temperature (such as in paramagnetism , but also other types of magnetism are possible). Magnetization follows Curie's law , according to which magnetization is inversely proportional to temperature. If the temperature falls below the critical temperature , the spin-glass phase is reached and the magnetization becomes practically constant . Their value is called " field cooled ". If the external magnetic field is switched off, the magnetization of the spin glass first drops rapidly to the remanent magnetization and then approaches zero more slowly (or a small fraction of the original magnetization, this is not yet known). This decrease is not exponential and is a characteristic of spin glasses. Measurements have shown continuous changes in magnetization on the order of days above the noise limit of the measuring devices. ${\ displaystyle T_ {f}}$ ${\ displaystyle T_ {f}}$

In contrast to spin glass, the magnetization of a ferromagnet drops to a certain value after switching off the external field (remanent magnetization), which remains constant over time. In the case of a paramagnet, the magnetization quickly drops to zero when the external field is switched off. In both cases the decrease occurs exponentially with a very small time constant .

If you cool a spin glass below the transition temperature without an external field and then bring it into a magnetic field, the magnetization rises quickly to the zero-field-cooled magnetization , which is lower than the " field-cooled magnetization " given above, and then approaches more slowly the Field-cooled value.

theory

In the theory of the spin glasses, strongly simplified models are used throughout, but these are intended to describe the essentials (a distinction is therefore made between relevant and irrelevant properties).

For example, in the Edwards-Anderson model, the spin glasses are described by a spin model with Ising degrees of freedom and interaction constants randomly distributed from place to place.Gaussian normal distributions are used as the random distribution , and only nearest-neighbor interactions are taken into account. ${\ displaystyle J_ {i, k} \ ,.}$

If one abandons the last-mentioned restriction, one obtains the strongly investigated Sherrington-Kirkpatrick model (after David Sherrington and Scott Kirkpatrick 1975).

The ± 1-spin glass is even simpler, assuming that we are only dealing with binary spin degrees of freedom of the kind , where positive and negative interactions are equally frequent with the same amount. ${\ displaystyle \ pm 1}$

Importance of Theory

Much of the early theoretical work on spin glasses uses some form of mean field theory based on a set of replicas of the state function of the system.

An important, apparently (!) Precisely solvable model of a spin glass was introduced by Sherrington and Kirkpatrick and led to considerable extensions of the mean field theory to describe the slow dynamics of magnetization and the complex, non- ergodic state of equilibrium .

Instead of the specified Sherrington and Kirkpatrick solution of their model occurred by Giorgio Parisi derived complicated result, with an order parameter - function instead of the usual simple order parameter . In this context, Parisi also found a special hierarchical procedure for “replica symmetry breaking ”, which has also been used in other contexts beyond the spin-glass theory (see below). ${\ displaystyle q (x)}$ ${\ displaystyle q}$

The non-ergodic behavior of the system below the freezing temperature is that at these temperatures the system “gets stuck” in the deep valleys of the resulting hierarchically disordered energy landscape. ${\ displaystyle T_ {f}}$

Applications

Although spin-glass magnetism typically only occurs below a temperature of about 30 Kelvin (≈ −240 degrees Celsius ) and thus appears to be completely useless in practice, it has in other contexts, e.g. B. in the theory of so-called neural networks , d. H. found application in theoretical brain research . The same applies to the mathematical and economic optimization theory .

literature

KH Fischer, JA Hertz: Spin Glasses . Cambridge University Press, Cambridge et al. 1991, ISBN 0-521-34296-1 , ( Cambridge studies in magnetism 1).
Marc Mézard , Giorgio Parisi , Miguel Virasoro : Spin Glass Theory and Beyond . World Scientific, Singapore et al. 1987, ISBN 9971-5-0115-5 , ( World scientific lecture notes in physics 9).
JA Mydosh: Spin Glasses. An experimental introduction . Taylor & Francis, London et al. 1993, ISBN 0-7484-0038-9 .
K. Binder , AP Young : Spin-Glasses. Experimental Facts, Theoretical Concepts, and Open Questions . In: Reviews of Modern Physics 58, 1986, ISSN 0034-6861 , pp. 801-976, doi : 10.1103 / RevModPhys.58.801 .
Erwin Bolthausen, Anton Bovier (editor): Spin Glasses . Springer Berlin 2010, ISBN 3-540-40902-5 , (Springer Lecture Notes in Mathematics)

References and comments

↑ J. Vannimenus, G. Toulouse: Theory of the frustration effect. II. Ising spins on a square lattice . In: Journal of Physics C: Solid State Physics . tape 10 , no. 18 , 1977, p. L537-L542 , doi : 10.1088 / 0022-3719 / 10/18/008 .
↑ ^a ^b A system of nothing but triangular spins with exclusively antiferromagnetic interactions between the nearest neighbors has an infinite number of frustrated triangular cells, but is still not called a spin glass because they are regularly arranged.
↑ The hierarchically disordered behavior of the energy landscape can be characterized verbally as follows: The main characteristics of the energy landscape are "deep valleys in even deeper valleys, in even deeper valleys, etc."

[1] J. Vannimenus, G. Toulouse: Theory of the frustration effect. II. Ising spins on a square lattice . In: Journal of Physics C: Solid State Physics . tape 10 , no. 18 , 1977, p. L537-L542 , doi : 10.1088 / 0022-3719 / 10/18/008 .

[Dreiecke-2] A system of nothing but triangular spins with exclusively antiferromagnetic interactions between the nearest neighbors has an infinite number of frustrated triangular cells, but is still not called a spin glass because they are regularly arranged.

[3] The hierarchically disordered behavior of the energy landscape can be characterized verbally as follows: The main characteristics of the energy landscape are "deep valleys in even deeper valleys, in even deeper valleys, etc."