Surreal number

Visualization of some surreal numbers

The surreal numbers are a class of numbers that includes all real numbers , as well as “infinitely large” numbers that are larger than any real number. Every real number is surrounded by surreal numbers that are closer to it than any other real number, in particular there are “infinitesimal” numbers that are closer to zero than any positive real number. In this they agree with the hyper-real numbers , but they are constructed in a substantially different way and contain the hyper-real numbers as a subset.

The word "surreal" comes from French and means "above reality". It is also used for the Surrealism style .

Surreal numbers were first introduced by John Conway and described in detail in 1974 in Donald E. Knuth's mathematical novel Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness . In his book, which is kept in dialogue form, Knuth coined the term surreal numbers for what Conway originally called just numbers . Conway liked the new name, so he later adopted it. He described the surreal numbers and used them to analyze games (including Go ) in his mathematics book On Numbers and Games (1976).

motivation

Surreal numbers are interesting structures for a number of reasons. On the one hand, they arise from two simple rules "out of nowhere" and still have properties similar to real numbers. We are forced to prove every statement that we take for granted about the real numbers, e.g. B. that holds or that it always follows. The surreal numbers are therefore a great way to practice methods of abstract algebra . Some applications in game theory were presented by Conway (see the section on game theory below). ${\displaystyle x\leq x}$ ${\displaystyle x=y}$ ${\displaystyle x+z=y+z}$

Finally, like the hyper-real numbers , the surreal numbers form a model of non-standard analysis in which e.g. B. infinitesimal numbers exist. Before we start to define surreal numbers, we should realize that we are starting with the construction of surreal numbers purely in set theory and that we do not know anything about number properties such as "smaller", zero, one, addition and multiplication.

construction

The basic idea behind the construction of the surreal numbers is similar to the Dedekind cuts . We create a new number by giving two sets and numbers that approximate the new number. The set consists of numbers that are smaller than the new number and is a set of numbers that are larger than the new number. We write such a representation as . We only make the condition of the sets and that every element of should be smaller than every element of . For example, a valid (“well-formed”) construction of a certain number is between and . (Which this is will be explained later.) It is expressly allowed that the sets are empty. The interpretation of the representation is "a number that is greater than any number in " and is "a number that is less than any number in ". The construction principle of the surreal numbers is, however, highly recursive; In addition to a construction rule, we also need a comparison rule for the recursively declared order relation ( less than or equal to ), which must be used for the application of the construction rule. ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle \{L|R\}}$ ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle \{\{1,2\}|\{5,8\}\}}$ ${\displaystyle 2}$ ${\displaystyle 5}$ ${\displaystyle \{L|\emptyset \}}$ ${\displaystyle L}$ ${\displaystyle \{\emptyset |R\}}$ ${\displaystyle R}$ ${\displaystyle \leq }$

Construction and comparison rule

Construction rule

If and are two sets of surreal numbers and no element of is less than or equal to an element of , then is a surreal number. Any surreal number can be described in this way. ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle L}$ ${\displaystyle \{L|R\}}$

Given a surreal number , we call the left set and the right set of . ${\displaystyle x=\{L_{x}|R_{x}\}}$ ${\displaystyle L_{x}}$ ${\displaystyle R_{x}}$ ${\displaystyle x}$

Comparison rule

For two surreal numbers and applies if less than or equal any element of and no element of less than or equal is. ${\displaystyle x=\{L_{x}|R_{x}\}}$ ${\displaystyle y=\{L_{y}|R_{y}\}}$ ${\displaystyle x\leq y}$ ${\displaystyle y}$ ${\displaystyle L_{x}}$ ${\displaystyle R_{y}}$ ${\displaystyle x}$

To simplify the notation, we leave out the set brackets and the empty set for the left and right sets, where no misunderstandings are to be feared, i.e. H. we write z. B. for or for . An object that fulfills the less than or equal condition is also called well-formed in order to distinguish it from objects considered later without this condition (the so-called games ). ${\displaystyle \{a,b\,|\,x\}}$ ${\displaystyle \{\{a,b\}|\{x\}\}}$ ${\displaystyle \{|a\}}$ ${\displaystyle \{\emptyset \,|\,\{a\}\}}$ ${\displaystyle \{L|R\}}$

These two rules are recursive, so we need some form of induction to work with them. One candidate would be complete induction , but as we shall see later, it is transfinite induction that makes things really interesting; H. if you apply these rules “more than finitely often”.

Relations

So that the objects created can be called numbers in a meaningful way, they should have a total order . However, the relation is only a total quasi-order , i.e. H. it is reflexive and transitive, but not antisymmetric (from and does not necessarily follow that ). To remedy this, we define a relation == on the surreal numbers: ${\displaystyle \leq }$ ${\displaystyle x\leq y}$ ${\displaystyle y\leq x}$ ${\displaystyle x=y}$

It applies exactly if and ${\displaystyle x==y}$ ${\displaystyle x\leq y}$ ${\displaystyle y\leq x.}$

This is an equivalence relation , and the equivalence classes are totally ordered. If and are in the same equivalence class, then they represent the same surreal number. We write the equivalence class of as , where is a representative of the class . So it's equivalent to . This procedure corresponds to the construction of the rational numbers as equivalence classes of fractions of whole numbers, the construction of the real numbers as equivalence classes of Cauchy sequences or the construction of the hyper-real numbers as equivalence classes of real sequences . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle [x]}$ ${\displaystyle x}$ ${\displaystyle [x]}$ ${\displaystyle x==y}$ ${\displaystyle [x]=[y]}$

Examples

Let us now consider some examples of surreal numbers. Since we don't yet know any surreal numbers, the only set we can take for and is the empty set. So our first number is ${\displaystyle L}$ ${\displaystyle R}$

${\displaystyle \{|\}=\{\emptyset |\emptyset \}}$

This number satisfies the design rule, since the empty set does not contain any element that could violate any condition. We call it and we write its equivalence class as 0. According to the comparison rule applies ${\displaystyle \mathbf {0} }$ ${\displaystyle [\mathbf {0} ]}$

${\displaystyle \mathbf {0} \leq \mathbf {0} }$.

By applying the construction rule, we get the numbers

${\displaystyle \{\mathbf {0} |\},\{|\mathbf {0} \}}$ and ${\displaystyle \{\mathbf {0} |\mathbf {0} \}}$

However, the last number is not a well-formed surreal number because of it . The numbers found so far can be sorted as follows: ${\displaystyle \mathbf {0} \leq \mathbf {0} }$

${\displaystyle \{|\mathbf {0} \}<\mathbf {0} <\{\mathbf {0} |\}}$

It means that does not apply. We call the new numbers and and their equivalence classes and . Since the equivalence classes so far only contain one element, we can also write this arrangement as ${\displaystyle x<y}$ ${\displaystyle y\leq x}$ ${\displaystyle \{|\mathbf {0} \}=:\mathbf {-1} }$ ${\displaystyle \{\mathbf {0} |\}=:\mathbf {1} }$ ${\displaystyle -1}$ ${\displaystyle 1}$

${\displaystyle -1<0<1}$.

If we apply the construction rule again in every possible way, we get not only some invalid numbers but also the well-formed surreal numbers

${\displaystyle \{|\mathbf {-1} \}==\{|\mathbf {-1} ,\mathbf {0} \}==\{|\mathbf {-1} ,\mathbf {1} \}==\{|\mathbf {-1} ,\mathbf {0} ,\mathbf {1} \}<}$

${\displaystyle \{|\mathbf {0} ,\mathbf {1} \}==\mathbf {-1} <}$

${\displaystyle \{\mathbf {-1} |\mathbf {0} \}==\{\mathbf {-1} |\mathbf {0} ,\mathbf {1} \}<}$

${\displaystyle \{\mathbf {-1} |\}==\{|\mathbf {1} \}==\{\mathbf {-1} |\mathbf {1} \}==\mathbf {0} <}$

${\displaystyle \{\mathbf {0} |\mathbf {1} \}==\{\mathbf {-1} ,\mathbf {0} |\mathbf {1} \}<}$

${\displaystyle \{\mathbf {-1} ,\mathbf {0} |\}==\mathbf {1} <}$

${\displaystyle \{\mathbf {1} |\}==\{\mathbf {0} ,\mathbf {1} |\}==\{\mathbf {-1} ,\mathbf {1} |\}==\{\mathbf {-1} ,\mathbf {0} ,\mathbf {1} |\}}$

We make three observations:

1. We have four new equivalence classes , , and . ${\displaystyle [\{|\mathbf {-1} \}]}$ ${\displaystyle [\{\mathbf {-1} |\mathbf {0} \}]}$ ${\displaystyle [\{\mathbf {0} |\mathbf {1} \}]}$ ${\displaystyle [\{\mathbf {1} |\}]}$
2. All equivalence classes now contain more than one element.
3. The value of a surreal number depends only on the largest element of its left set and the smallest element of its right set.

The first observation leads us to the question of how these new equivalence classes are to be interpreted. Since is less than , we call it and its equivalence class . The number is called , is between and , and we call them , and we call . We write the equivalence classes as , , and . We get a further reason for these designations when we have defined the addition and multiplication. ${\displaystyle \{|\mathbf {-1} \}}$ ${\displaystyle -1}$ ${\displaystyle \mathbf {-2} }$ ${\displaystyle -2}$ ${\displaystyle \{\mathbf {1} |\}}$ ${\displaystyle \mathbf {2} }$ ${\displaystyle \{\mathbf {-1} |\mathbf {0} \}}$ ${\displaystyle -1}$ ${\displaystyle 0}$ ${\displaystyle \mathbf {-1/2} }$ ${\displaystyle \{\mathbf {0} |\mathbf {1} \}}$ ${\displaystyle \mathbf {1/2} }$ ${\displaystyle -2}$ ${\displaystyle 2}$ ${\displaystyle -1/2}$ ${\displaystyle 1/2}$

The second observation leads us to ask whether we can still identify a surreal number with its equivalence class. The answer is positive because you can show:

If and then . ${\displaystyle [L_{x}]=[L_{y}]}$ ${\displaystyle [R_{x}]=[R_{y}]}$ ${\displaystyle [\{L_{x}|R_{x}\}]=[\{L_{y}|R_{y}\}]}$

Here is the set of equivalence classes of elements of . So we can rewrite the listing from above too ${\displaystyle [X]=\{[x]:x\in X\}}$ ${\displaystyle X}$

${\displaystyle \{|-1\}=\{|-1,0\}=\{|-1,1\}=\{|-1,0,1\}=:-2<}$

${\displaystyle \{|0,1\}=-1<}$

${\displaystyle \{-1|0\}=\{-1|0,1\}=:-1/2<}$

${\displaystyle \{-1|\}=\{|1\}=\{-1|1\}=0<}$

${\displaystyle \{0|1\}=\{-1,0|1\}=:1/2<}$

${\displaystyle \{-1,0|\}=1<}$

${\displaystyle \{1|\}=\{0,1|\}=\{-1,1|\}=\{-1,0,1|\}=:2}$

or shorter

${\displaystyle -2<-1<-1/2<0<1/2<1<2}$.

The third observation can be generalized to any surreal number with finite left and right sets. The number mentioned above is therefore the same and will be specified in more detail later. Infinite sets do not have to contain a largest element, so only a modified statement applies to numbers with infinite sets. ${\displaystyle \{1,2|5,8\}}$ ${\displaystyle \{2|5\}}$

Calculating with surreal numbers

The addition and multiplication of surreal numbers is defined by the following three rules:

addition

${\displaystyle x+y=\{(L_{x}+y)\cup (x+L_{y})\;|\;(R_{x}+y)\cup (x+R_{y})\}}$

negation

${\displaystyle -x=\{-R_{x}\,|\,-L_{x}\}}$

multiplication

${\displaystyle x\cdot y=\{(L_{x}\cdot y+x\cdot L_{y}-L_{x}\cdot L_{y})\,\cup \,(R_{x}\cdot y+x\cdot R_{y}-R_{x}\cdot R_{y})\;|\;(L_{x}\cdot y+x\cdot R_{y}-L_{x}\cdot R_{y})\,\cup \,(R_{x}\cdot y+x\cdot L_{y}-R_{x}\cdot L_{y})\}}$.

Here we use the set-theoretical extension of the operators , i. H. it mean for example ${\displaystyle +,-,\cdot }$

${\displaystyle X+y=\{x+y:x\in X\}}$,

${\displaystyle -X=\{-x:x\in X\}}$

and

${\displaystyle X+Y=\{x+y:x\in X,\,y\in Y\}}$

These links are well-defined in the sense that the link from well-formed surreal numbers is again a well-formed surreal number; H. a number whose left set is “smaller” than the right set.

With these arithmetic rules, we can now determine that the names assigned so far match, because it applies, for example

${\displaystyle \mathbf {0} +\mathbf {0} =\mathbf {0} }$, , And . ${\displaystyle \mathbf {1} +\mathbf {1} =\mathbf {2} }$ ${\displaystyle -(\mathbf {1} )=\mathbf {-1} }$ ${\displaystyle \mathbf {1/2} +\mathbf {1/2} ==\mathbf {1} }$

(Note the distinction between the equality " " and the equivalence " "!) ${\displaystyle =}$ ${\displaystyle ==}$

The links can be transferred to the equivalence classes because

From and follows and and . ${\displaystyle [x]=[x']}$ ${\displaystyle [y]=[y']}$ ${\displaystyle [x+y]=[x'+y']}$ ${\displaystyle [-x]=[-x']}$ ${\displaystyle [x\cdot y]=[x'\cdot y']}$

they are also well-defined combinations of the equivalence classes. Finally, one can show that the links between the equivalence classes have nice algebraic properties:

The equivalence classes together with the order and the algebraic connections fulfill all the properties of an ordered field , but they are not a set, but a real class and therefore not an ordered field in the sense of its definition.

In the following we no longer differentiate between a surreal number and its equivalence class, so we call the equivalence class itself a surreal number.

Generation by complete (finite) induction

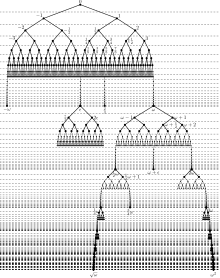
So far we have not looked systematically to see which numbers we get from the construction rule and which we don't. We start with the numbers that we can achieve in a finite number of steps. We do this inductively by defining sets for every natural number as follows: ${\displaystyle S_{n}}$ ${\displaystyle n}$

• ${\displaystyle S_{0}=\{0\}}$
• ${\displaystyle S_{i+1}}$is the set together with all surreal numbers that are generated from subsets of in one construction step. ${\displaystyle S_{i}}$ ${\displaystyle S_{i}}$

We call the set of all surreal numbers that lie in any one . The first sets of surreal numbers are ${\displaystyle S_{i}}$ ${\displaystyle S_{\omega }}$

${\displaystyle S_{0}=\{0\}}$

${\displaystyle S_{1}=\{-1<0<1\}}$

${\displaystyle S_{2}=\{-2<-1<-1/2<0<1/2<1<2\}}$

${\displaystyle S_{3}=\{-3<-2<-1\,1/2<-1<-3/4<-1/2<-1/4<0<1/4<1/2<3/4<1<1\,1/2<2<3\}}$

We observe two things:

1. In each step the maximum increases and the minimum decreases . ${\displaystyle 1}$ ${\displaystyle 1}$
2. In each step we find a new number between two neighboring numbers.

A corollary of this is that in this way we can produce exactly all dyadic fractions ; H. any rational number of form

${\displaystyle a/2^{b}}$

with an integer and a natural number is in . However, we will other fractions such as , , , in any place as long as a natural number. What one could take for instead , we come to in the next section. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle S_{\omega }}$ ${\displaystyle 1/3}$ ${\displaystyle 2/3}$ ${\displaystyle 1/5}$ ${\displaystyle 1/6}$ ${\displaystyle S_{n}}$ ${\displaystyle n}$ ${\displaystyle n}$

"To infinity and beyond"

Now that we have another set of surreal numbers, nothing prevents us from applying the construction rule to them and constructing sets , etc. The quantities on the left and right of surreal numbers can now become infinitely large. ${\displaystyle S_{\omega }}$ ${\displaystyle S_{\omega +1}}$ ${\displaystyle S_{\omega +2}}$

In fact, we can use transfinite induction to define a set of surreal numbers for each ordinal number . ${\displaystyle a}$ ${\displaystyle S_{a}}$

The smallest ordinal number such that a surreal number is included in the set is called the birthday of . For example, is the birthday of and is the birthday of . ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle S_{a}}$ ${\displaystyle x}$ ${\displaystyle 0}$ ${\displaystyle 0}$ ${\displaystyle 2}$ ${\displaystyle 1/2}$

It can be shown that the expression for surreal numbers represents the “oldest” surreal number between and . The above number is the same and the oldest number between and is the , so . ${\displaystyle \{\{a\}|\{b\}\}}$ ${\displaystyle a<b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \{\{1,2\}|\{5,8\}\}}$ ${\displaystyle \{2|5\}}$ ${\displaystyle 2}$ ${\displaystyle 5}$ ${\displaystyle 3}$ ${\displaystyle \{2|5\}==3}$

Already in we find the breaks that we still lacked in. For example is ${\displaystyle S_{\omega +1}}$ ${\displaystyle S_{\omega }}$

${\displaystyle \mathbf {1/3} =\{\{a/2^{b}\in S_{\omega }|3a<2^{b}\}|\{a/2^{b}\in S_{\omega }|3a>2^{b}\}\}}$.

The correctness of this definition follows from the equivalence

${\displaystyle \mathbf {3} \cdot (\mathbf {1/3} )==\mathbf {1} }$.

The birthday of is . ${\displaystyle 1/3}$ ${\displaystyle \omega +1}$

In all real numbers are included. This can be illustrated by the fact that each nesting of intervals defines exactly one real number and that every real number can be represented by nesting intervals. Now all numbers with the representation ( any whole numbers) are already included in. In addition, with these numbers as limits, you can already find interval nestings for all real numbers. Now take the lower limits of this interval nesting in the left set and the upper limits of the interval nesting in the right set and you have the desired real number as part of . ${\displaystyle S_{\omega +1}}$ ${\displaystyle k/2^{j}}$ ${\displaystyle k,j}$ ${\displaystyle S_{\omega }}$ ${\displaystyle S_{\omega +1}}$

Another number that lies in is ${\displaystyle S_{\omega +1}}$

${\displaystyle \mathbf {\varepsilon } =\{0|...,1/16,1/8,1/4,1/2,1\}}$.

It's easy to see that this number is greater than but less than any positive fraction. So it is an infinitesimal number . We therefore denote their equivalence class with . This is not the only infinitesimal number. B. ${\displaystyle 0}$ ${\displaystyle \varepsilon }$

${\displaystyle 2\varepsilon =\{\varepsilon |\ldots ,\varepsilon +1/16,\varepsilon +1/8,\varepsilon +1/4,\varepsilon +1/2,\varepsilon +1\}}$,

${\displaystyle \varepsilon /2=\{0|\varepsilon \}}$.

However, these numbers are only in . ${\displaystyle S_{\omega +2}}$

In addition to infinitely small numbers, infinitely large numbers can also be found in, such as B. ${\displaystyle S_{\omega +1}}$

${\displaystyle \mathbf {w} =\{S_{\omega }|\}}$.

This number is greater than any number in , especially greater than any natural number, so we denote its equivalence class with . This number corresponds to the ordinal number . It is also ${\displaystyle S_{\omega }}$ ${\displaystyle \omega }$ ${\displaystyle \omega }$

${\displaystyle \mathbf {w} ==\{1,2,3,4,\ldots |\}}$.

You can even represent any ordinal number as a surreal number.

Since addition and subtraction are explained for all surreal numbers, we can calculate with as with any other number and z. B. Calculate the following: ${\displaystyle \omega }$

${\displaystyle \omega +1=\{\omega |\}}$ and

${\displaystyle \omega -1=\{S_{\omega }|\omega \}}$.

This also works for larger summands:

${\displaystyle \omega +2=\{\omega +1|\}}$,

${\displaystyle \omega +3=\{\omega +2|\}}$,

${\displaystyle \omega -2=\{S_{\omega }|\omega -1\}}$,

${\displaystyle \omega -3=\{S_{\omega }|\omega -2\}}$

and even with yourself: ${\displaystyle \omega }$

${\displaystyle \omega +\omega =\{\omega +S_{\omega }|\}}$

where as above. ${\displaystyle x+Y=\{x+y|y\in Y\}}$

Just as is greater than is less than , because ${\displaystyle 2\cdot \omega =\omega +\omega }$ ${\displaystyle \omega }$ ${\displaystyle \omega /2}$ ${\displaystyle \omega }$

${\displaystyle \omega /2=\{S_{\omega }|\omega -S_{\omega }\}}$

whereby . ${\displaystyle x-Y=\{x-y|y\in Y\}}$

Finally we find a close connection between and , for it is ${\displaystyle \omega }$ ${\displaystyle \varepsilon }$

${\displaystyle \varepsilon \cdot \omega =1}$.

It should be noted, however, that the calculation rules for ordinal numbers differ from those for surreal representations: In ordinal numbers, however , is as a surreal number . ${\displaystyle 1+\omega =\omega <\omega +1}$ ${\displaystyle 1+\omega =\omega +1>\omega }$

A great many numbers can be produced in this way, even so many that no set can hold them all. The surreal numbers, like the ordinal numbers, form a real class .

Since every surreal number is composed of surreal numbers that have a smaller birthday, almost all statements about surreal numbers can be proven by transfinite induction. One shows that a statement holds for if it holds for every element of and . ${\displaystyle x=\{X_{L}|X_{R}\}}$ ${\displaystyle X_{L}}$ ${\displaystyle X_{R}}$

Set theoretical remark

As already mentioned in the section Calculating with surreal numbers , the surreal numbers form a real class, i.e. not a set in the sense of a common set theory such as the Zermelo-Fraenkel set theory . The reason is that every ordinal number can be represented as a surreal number and the ordinal numbers already form a real class. The definition of a surreal number as a pair of left set and right set of surreal numbers excludes that one of these sets could also be a real class, since sets cannot be real classes.

Generalization: Games

The definition of a surreal number contained one restriction: each element of must be less than each element of . If you drop this restriction, you get a larger class of objects Games (Engl. For games ) are called. A game is created by applying this rule: ${\displaystyle L}$ ${\displaystyle R}$

Construction rule

If and are two sets of games , then there is a game . ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle \{L|R\}}$

Comparison, equivalence, addition, negation and multiplication are defined in the same way as for surreal numbers.

Every surreal number is a game , but there are also non-well-formed games , such as B. . The class of games is more general than that of surreal numbers and has a simpler definition, but it lacks some of the beautiful properties of surreal numbers. The games do not form a body. They only have a partial order , i.e. H. there are games that are not comparable. Every surreal number is either greater, equal, or less than , but a game is either greater, equal, less than, or incomparable with ( fuzzy ). Are , , surreal numbers , then . If , on the other hand , are games with , then this does not always apply . ${\displaystyle \{\mathbf {0} |\mathbf {0} \}}$ ${\displaystyle 0}$ ${\displaystyle 0}$ ${\displaystyle 0}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle x==y}$ ${\displaystyle x\cdot z==y\cdot z}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle x==y}$ ${\displaystyle x\cdot z==y\cdot z}$

Surreal numbers and game theory

The surreal numbers were originally motivated by studying the game Go , and there are many connections between popular games and surreal numbers.

We consider games with the following properties:

• Two players, called Left and Right
• Deterministic (no dice or shuffled cards)
• No hidden information (such as face-down playing cards)
• The players take turns drawing.
• After a finite number of moves, each game ends with the victory of a player.
• If a player can no longer make a move, the game ends and that player loses (the game may end in a draw in chess ).

Such games are chess, checkers , mills and go , but not most card games, memory or “ don't get angry ”.

In most games, neither player has a big advantage initially. However, if the game progresses, then at some point situations arise in which one of the players has a clear advantage. To analyze a game, it now classifies every possible game situation game to. The value of a game position is the game , which includes the values ​​of all positions that can be reached by a move from the left and the values ​​of all positions that can be reached by a move from the right . This simple way of linking games with game positions produces interesting results. Let us assume that two perfect players are in a game situation whose game is. Then the winner of the game is certain: ${\displaystyle \{L|R\}}$ ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle x}$

• Is , then links wins , ${\displaystyle x>0}$
• is , then gains the right , ${\displaystyle x<0}$
• is then lose the player who is on the train, ${\displaystyle x=0}$
• is fuzzy , then the player whose turn it is wins. ${\displaystyle x}$

Sometimes as a game nears the end it breaks down into smaller parts that are completely independent. In the game of Go, for example, the game board is gradually divided between the parties until only small, separate islands of neutral space remain in which the players can place bets. Each island behaves like its own game of Go on a very small board. It would now be useful to analyze each sub-lot individually and then be able to combine the results in order to get an analysis of the whole lot. It's not an easy task. For example, you could have two sub-games in which the attracting player wins, but if you look at both games together, the other player wins. However, there is a way to do this analysis and that is by the following theorem:

If a big game is divided into two smaller, independent games and the two games have the games and , then the big game has the game . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x+y}$

In other words: combining several independent games is the same as adding up your games .

historical development

Conway developed the theory of surreal numbers in the reverse order of the representation chosen here. He analyzed endgames in Go and looked for a way to combine the analyzes of independent subgames. He developed the concept of games, also known as combinatorial game theory , with the options of addition, negation and size comparison. Eventually he noticed that a certain class of games (later called surreal numbers) had interesting properties and found a multiplication for them that satisfies the axioms of the body and by which they contain the real numbers.

Web links

• A simple kept, yet thorough introduction by Claus Tøndering (English)