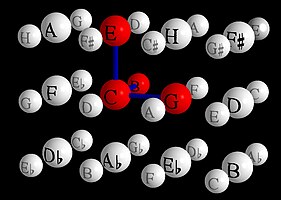
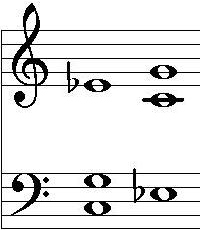Vogel's clay net
The Vogelsche Tonnetz is a graphic and mathematical representation of the sound supply of the pure tuning , which was proposed by the music theorist Martin Vogel in 1976 in his work "The theory of tone relationships". The graphic representation is based on Euler's tone net , whereby a third dimension for pure sevenths ( natural sevenths ) is added to the two dimensions for perfect fifths and pure thirds . Its main purpose is to display and analyze chords and chord relationships. The four-dimensional mathematical representation enables the evaluation of the overtone fit of chords depending on the tone set used and thus also statements about the optimal tone set for a certain chord.
The graphic representation
The graphical representation of the tone network is limited to the three dimensions for fifths, thirds and sevenths. In this representation, octave-related tones are shown on the same nodes. The figure shows the representation of the four-tone four-tone system, which is statistically most common in Western music, the seventh chord , in the two-dimensional Euler's tone network with a B formed using fifths and thirds and in the three-dimensional Vogelian tone network with a natural seventh .
The representation in the three-dimensional tone network with the natural septime makes the statistical dominance of this four-tone representation appear much more plausible than the two-dimensional representation: There is a clear reference note (C), from which all other tones can be seen as a simple one (meaning: not combined from several intervals ) Interval results: fifth up, third up, seventh up.
The mathematical representation
The mathematical representation of tone relationships in Vogel's tone network is four-dimensional, as octaves are also taken into account. Each tone is represented by a quadruple of numbers that indicate how many octaves, "fifths", "thirds" and "sevenths" are required to get from a defined starting point to this tone in the tone network (where "fifths" , "Thirds" and "Seventh" stand for the prime numbers 3, 5 and 7, not for the intervals 3/2, 5/4 and 7/4). For example, the C major seventh chord shown above with the notes c ', e', g 'and b' (viewed from the C of the major octave) could be represented by the numbers 4, 5, 6 and 7 and thus by the quadruples (2nd , 0,0,0), (0,0,1,0), (1,1,0,0) and (0,0,0,1) can be represented. The quadruple notation thus represents the prime factorization of the numbers occurring in the chord description for the first four prime numbers.
Vogel adopts Arthur von Oettingen's dual tone system , in which major and minor chords are interpreted as reciprocal mirror images. He extends this view to include a quantitative calculation of consonance (or rather dissonance) values.
To do this, he introduces virtual reference tones that are not necessarily present in the chord, to which all the tones present in the chord are in unbroken integer relationships. For every chord represented in the tone network, there is a low reference tone (all tones can be represented as multiples of the frequency of this reference tone) and a high reference tone (the reference tone for each chord tone can be represented as an integral multiple of its frequency). In the quadruple notation, a chord thus contains only positive values in relation to its lower reference tone, and only negative values in relation to the upper reference tone in the quadruples which describe the chord tones. All prime numbers occurring in the description of the relationships between the chord tones and their reference tone are added up weighted. For the prime numbers 2, 3, 5 and 7, Vogel suggests the weights 1, 3, 5 and 7. The more obvious variant, in which the prime number 2 is also weighted with its own numerical value, is rejected by Vogel because it leads to results that, in his opinion, do not match the listening experience. The sum of the prime weights is then divided by the number of tones in the chord. This calculation is carried out for both the upper and the lower reference tone. The smaller of these two numerical values decides whether it is an upper sound or a lower sound.
The C major triad c'-e'-g 'in the dashed octave can be related, for example, to the low reference note C from the large octave; The three tones of the triad are related to this in integer ratios (4, 5 and 6). The prime factorization gives 2 · 2.5.2 · 3. With the weights suggested by Vogel, a consonance value of (1 + 1 + 5 + 1 + 3) / 3 = 11/3 = 3.67 results. The same chord can also be related to the four-stroke h '' '': this upper reference note has fifteen times the frequency of c ', twelve times the frequency of e' and ten times the frequency of g '. The prime factorization gives 3 x 5.2 x 2 x 3.2 x 5. This results in a consonance value of (3 + 5 + 1 + 1 + 3 + 1 + 5) / 3 = 19/3 = 6.33. The consonance value for the lower reference tone is more favorable; thus the C major triad is an overtone over C. For the C minor triad c'-es'-g 'the consonance value is the same, but based on the upper reference note g' ''. Thus, in Vogel's music theory, this chord is not related to C ("C minor"), but to G (sub-sound under G).
Vogel suggests a special notation for ascenders and descenders. Upper notes are marked with an O, lower notes with a U. The reference tone is given as a lowercase letter. Ascenders are noted from left to right, descenders from right to left. This results in the notation cO for the C major chord and Ug for the C minor chord. Further symbols for additional tones (e.g. a 7 for an upper or lower seventh) are accordingly added to the right for upper sounds and left for lower sounds. The C 7 chord from the first figure would therefore be noted as cO7.
Vogel also suggests a calculation for the consonance of chord transitions (when transitioning from an N-sound to an M-sound, all N · M transitions are evaluated individually by prime number decomposition and weighted sum, then the average is formed) and of entire pieces of music Inclusion of a central reference tone in the sense of a final .
Consonance and overtone fit
Martin Vogel's consonance formula should actually be called dissonance formula, because the higher the dissonance of a chord or interval, the higher the calculated value. Vogel did not claim to predict consonant judgments of today's listeners. This is countered by the fact that consonant judgments strongly correlate with familiarity judgments, that major and minor are today ascribed emotional tones (minor = sad), and that his formula only takes into account the fit of overtones , but not the fit of combination tones . To put it more cautiously, one could say that Vogel's consonance formula expresses a kind of overtone fit, i.e. is a measure of the extent to which the overtones of a chord fit together. Here, too, the validity of the formula is restricted by the limits of human hearing. A pure octave cannot be distinguished from an octave detuned by a schism (frequency difference about 2 cents ), since the limit of human perception for pitch differences of complex tones is about 0.25% (4 cents). Vogel's consonance formula, however, gives a consonance value of (1 · 1 + 0 · 3 + 0 · 5 + 0 · 7) / 2 = 0.5 for the pure octave (1,0,0,0), and for around one Schisma too large octave (-14,8,1,0) has a value of (14 1 + 8 3 + 1 5 + 0 7) / 2 = 43/2 = 21.5.
Consequences for the tone selection
With the help of the consonance value calculation it can be decided which tones should be taken from the tone stock for a chord. So z. B. the consonance value for the seventh chord in the two-dimensional Euler's tone network (see figure above) 8.5. If, on the other hand, one takes a natural seventh for the B, the consonance value improves to 4.5. The seventh chord with a natural seventh is therefore preferable to a seventh chord tuned only with fifths and thirds.
Consequences in terms of composition
If one follows the evaluations of Vogel's consonance formula, then there are consequences for how major and minor chords have to be set. In major chords, thirds and especially sevenths have to be set high if the chord is to sound consonant. With minor chords it is exactly the opposite. However, this in no way corresponds to the compositional practice of the last centuries (apart from the Tristan chord, see below), consequently minor chords placed in this way sound unusual. In fact, they are characterized by a much better fit of the overtones. For example, the left of the two C minor chords in the illustration opposite is set in the classic way with a major third: this leads to a consonance value of 4.33. The right chord with the low minor third sounds unusual, but it has a much better consonance value of 3.0 and a much better harmonic fit.
Limitation to the prime numbers 2, 3, 5 and 7
Vogel regards the theoretically infinite four-dimensional clay stock of his clay network as complete; he rules out further dimensions for higher prime numbers . According to Vogel, the consonance aimed for in the pure tuning is based on correspondences in the overtone series ; the next higher prime number (11) can no longer lead to an audible match, since only the first eight to ten partials are separated in the inner ear . A z. B. The eleventh partial tone isolated by means of a flageolet can be heard quite well and clearly distinguishable from the tenth or twelfth, but in a complex tone with all the partial tones of varying strength, these partials would merge and a match could no longer be determined. It would be interesting to check whether this is possible for instruments with predominantly odd partials, since the distances between the partials are larger here. With a little practice, consonances up to the prime number 17 or even 19 could theoretically become audible.
The half diminished seventh chord in Vogel's sound net
The Tristan chord is a music-historically significant chord in Richard Wagner's musical drama "Tristan und Isolde". It cannot be clearly interpreted as being functionally harmonious. It is seen as tonally unsteady and extremely chromatic.
In Vogel's Tonnetz, this chord is presented as a dual equivalent of the seventh chord, i.e. as the minor counterpart of a major seventh chord. This interpretation is not only supported by the resolution of this "G sharp minor chord with sub-seventh" into an E major chord with upper seventh (see also the animation on the left), but also Wagner's compositional technique, whereby the lower terez (H) and the lower seventh (F, actually E ♯ ) can be set deep. In bird notation 7UD would be for that chord ♯ to write, since the reference note of G # minor chord, the Dis (D ♯ is), all other notes unfold from which the overtones. Assuming that the consistent notation according to the dual system (a G sharp minor chord, G ♯ m, would have to be notated as a D flat sub-sound Ud ♯ ) will not prevail, then it would be a compromise, the Tristan chord notated as a slash chord G ♯ m / F, i.e. as a G sharp minor chord with an F in the bass.
The “explanation” of the Tristan chord in Vogel's Tonnetz as a well-placed minor counterpart to a major seventh chord cannot be compared with an “explanation” in terms of functional harmony. Both explanations cannot really justify causally why certain chords and chord progressions have established themselves in music history. While the functionally harmonious approach is primarily aimed at the relation of the chords to a tonality and thus gets into difficulties in late Romantic music with the loss of a consistent tonality, the explanatory approach of the Vogelsche Tonnetz mainly relates to the suitability of the notes of a chord to one another or to one another. to the notes of the preceding or following chord. Here at least it becomes clear that the Tristan chord is not an attack on tonality, but respects it just as much as a major seventh chord.
In jazz harmonic this chord corresponds to a half diminished seventh chord above F (as a chord symbol Fm 7 b5 ). This description does not reveal the connection with a G sharp minor chord. It results from the custom, which has become standard, of describing chords starting from the lowest note. In Vogel's theory, this is appropriate for ascenders, but not descenders: these must be described from top to bottom. It should be noted that the principle of the lowest note is not adhered to even with inversions of simple chords; otherwise a C major chord in the first inversion would have to be described as an E minor chord with an altered fifth (Em +5 ). Even the Tristan chord is not simply described in Vogel's system from the highest note (G ♯ ); the root position of the D ♯ in the barrel network is more important .
reception
Vogel's Tonnetz is based on a theory (Euler's Tonnetz) that is more than 100 years older than the currently dominant functional harmony. Although these two theories in no way contradict each other, rather complement each other (the sound network with its focus on local contexts and moods, the functional harmony with the attempt to classify the global function of a chord related to the entire piece), the otherness of the Theory and the idiosyncrasy of Vogel's chord notation their general reception. Vogel's consonance calculation has only recently become the subject of empirical studies. As a simplified notation, Kaernbach suggests always writing from left to right, using capital letters for the reference tones (to avoid confusion with the convention of identifying minor with lower case) and using triangles to mark the upper and lower lengths (▲ and ▼). The beginning of the Tristan foreplay would be z. B. to be noted as D ▼ ♯ 7 → E ▲ 7.
literature
- Martin Vogel: The Tristan Chord and the Crisis of Modern Harmony. Düsseldorf 1962.
- Martin Vogel: The theory of tone relationships. Bonn 1976.
Individual evidence
- ^ A b Agnieszka Karas, Christian Kaernbach: Putting Martin Vogel to test: An attempt to evaluate a musical theory. In U. Ansorge et al. (Ed.): Contributions to the 55th conference of experimental psychologists. ( Page no longer available , search in web archives ) Info: The link was automatically marked as defective. Please check the link according to the instructions and then remove this notice. (PDF; 11.3 MB) Pabst Science Publishers, Lengerich, 2013, p. 43.
- ^ A b Christian Kaernbach, Christian Bering: Exploring the temporal mechanism involved in the pitch of unresolved harmonics. In: Journal of the Acoustical Society of America. Vol. 110, 2001, pp. 1039-1048 ( PDF ).
- ^ Ernst Kurth: Romantic harmony and its crisis in Wagner's "Tristan", Bern 1920.
- ^ Christian Kaernbach: Honoring Martin Vogel - Champion of just intonation in music. In U. Ansorge et al. (Ed.): Contributions to the 55th conference of experimental psychologists. ( Page no longer available , search in web archives ) Info: The link was automatically marked as defective. Please check the link according to the instructions and then remove this notice. (PDF; 11.3 MB) Pabst Science Publishers, Lengerich, 2013, p. 43.