White noise
White noise is noise with a constant power density spectrum in a specific frequency range. White noise is perceived as a high-pitched noise (see psychoacoustics ). White, bandwidth- restricted noise is often used in engineering and natural sciences to map disturbances in an otherwise ideal model, e.g. B. to describe random interference in a transmission channel.
description
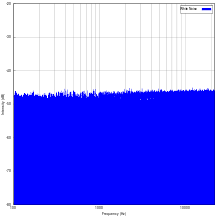
A constant power density spectrum is characteristic of white noise :
According to the Wiener-Chintschin theorem , the autocorrelation function of the white noise is therefore the delta distribution :
The autocorrelation function of white noise is a Dirac pulse . This means that the noise at a certain point in time is uncorrelated to all other points in time , since the autocorrelation is zero for these points in time.
White noise is also known as time-discrete signals , the individual sample values of which are uncorrelated.
In the bandwidth unlimited white noise is a model borderline case with infinitely high power and therefore does not occur in practice. In real systems, white noise only ever occurs in one frequency range with a constant power density spectrum in this range. The power density spectrum outside this bandwidth always falls towards 0 if the frequencies are only sufficiently high.
White noise can occur with different probability distributions of the signal amplitude . A common distribution is the normal distribution or also the Gaussian distribution, which is used in signal processing to describe the interference of transmission channels. In these channels, the noise is introduced as an additive disturbance variable and then referred to as additive white Gaussian noise . Also, thermal noise of electrical resistances can be primarily described by white Gaussian noise. In principle, white noise can also occur in other distributions, for example in the Cauchy or Poisson distribution .
Areas of application
In psychoacoustics , white noise is used to combat noise and in the area of tinnitus retraining therapy as a masker; Noise and other background noises are subjectively perceived as less loud and annoying if they are overlaid with white noise. Noise, in which all frequency components sound roughly equally loud, is called 1 / f noise . It has a power density spectrum that decreases with frequency.
In stochastics , white noise describes a discrete stochastic process of uncorrelated random variables with an expected value of 0 and constant variance . It is weakly stationary and has a constant spectral density . The white noise represents the simplest stochastic process, but many more complex processes and time series are constructed from such, such as the random walk or ARMA processes .
Color analogy of the name
The term white noise is to be understood in analogy to white light , in which different optical frequency components are superimposed to form a white color impression. However, light that is subjectively perceived as white by humans does not have a constant power density spectrum.
The terms red noise and pink noise were formed with a comparable color analogy .
literature
- Rudolf Müller: Noise . 2nd Edition. Springer, 2013, ISBN 978-3-540-51145-8 .
- Horst Stöcker (Ed.): Pocket book of physics. Formulas, tables, overviews. 4th edition. Harry Deutsch, 2000, ISBN 3-8171-1628-4 .
- Gopinath Kallianpur: White Noise Theory of Prediction, Filtering and Smoothing . CRC Press Inc., 1988, ISBN 978-2-88124-685-2 .



![{\ displaystyle r _ {\ eta \ eta} (\ tau): = \ operatorname {E} [\ eta (t) \ eta (t- \ tau)] = \ int _ {- \ infty} ^ {\ infty} S (f) e ^ {\ mathrm {j} 2 \ pi f \ tau} df = {\ text {const}} \ cdot \ delta (\ tau).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e4527b3e0a776a345697dc4380ca870a680eb17)


