Aberration (astronomy)
In astronomy, the aberration of light (from the Latin aberratio "deflection") describes a small apparent change in the location of all stars , caused by the finite speed of light when the observer moves sideways . In addition, the theoretical explanation of this effect was of great importance in the history of special relativity .
Types of aberration
This effect, also known as stellar aberration , affects the star locations in three ways:
- Annual aberration : The largest annual aberration angle is reached when the earth moves exactly perpendicular to the direction of the light beam coming from the star. As it approaches or moves away from the star, the angle of aberration is smaller. Therefore each star describes a small ellipse with a diameter of 41 ″ in relation to the celestial coordinate system ; only with stars vertically above or below the earth's orbit (see ecliptic ) is this change of direction circular. Its mean radius of exactly 20.49552 "is called the aberration constant and is of great importance for the fundamental system of astronomy (see also Simon Newcomb ).
- The daily aberration due to the earth's rotation can also be determined, but even at the equator it is only about 1.6 percent of the annual aberration. For a star in the meridian it is 0.32 ″ · cos B, depending on the latitude B of the location, and shifts the apparent star location to the east by this amount.
- The secular aberration is not periodic but a kind of perspective effect. Using stellar statistics methods , it was found in the 19th century that the “ fixed stars ” move slightly differently on opposite halves of the sky. The so-called apex can be calculated from this: the vanishing point in the constellation Hercules towards which the sun and our planetary system are moving at 20 km / s. However, the entire solar environment rotates at about 220 km / s around the center of mass of the Milky Way in the constellation Sagittarius .
There is also a planetary aberration . This is the case when the position and speed of the measured celestial body are known exactly during the emission of the light, as is the case with the planets of the solar system. In this way, the position of the planet at the point in time when the light reaches the observer can be calculated from the aberration angle and time corrections.
Explanation
General aberration
The difference in the direction of propagation of light in different inertial systems is most easily explained using the particle theory of light. The relationships here are similar to those of a moving observer who wants to determine the direction of the raindrops raining down on him.
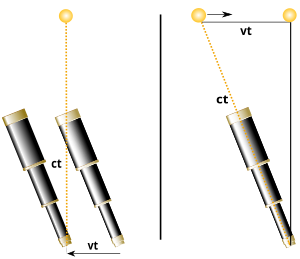
Let there be an inertial system in which a light beam emerges perpendicularly from a light source. (The light source of clarity is initially assumed to be at rest in this system, for reasons that the circumstances at a Lightwatch or the vertical arm of a Michelson interferometer dignity corresponds.) In addition to rest a telescope in the same inertial system, one would have it accurately in the perpendicular direction bringing to observe the light source. On the other hand, if the telescope moves at one speed , it must be tilted in the direction of movement in order to keep the light beam in its center (picture on the left), because the light needs a certain time to pass through the telescope. On the other hand, in the telescope's inertial system, the observer gets the impression that the rays arrive at an incline, and the light source does not appear in its actual direction , but rather shifted by a small aberration angle in the direction of the telescope movement (right image). The corresponding aberration formula for determining the relative angles in mutually moving inertial systems is derived using the relativistic addition of speed (see derivation).
Stellar aberration
The relativistic aberration formula generally applies to the transition from one inertial system to another, regardless of whether the light source is in one of these systems or not. For example, in astronomical observations, the light sources are stars or star systems, the exact state of which is often not known. Because of the great distance, these shrink to very small or even point-like objects, whose movements are too small to change their relative positions in the night sky significantly (" fixed stars "). From the point of view of an observer resting near the sun, the light from a distant star system would always flow in at approximately the same angle. Even high speeds within the observed star system (such as the opposing movements of double stars ) do not change this fact, since only those rays of light are of importance here, which propagate in a straight line from the double star system at exactly the same angle to reach the observer at all . To determine the direction of a beam, only the relative location of the emission and the location of the receiver play a role. For this reason, the idea that sometimes occurs that the stellar aberration angle depends on the actual proper movement of the light source ("active aberration") must be rejected. This fact was pointed out by Herschel in 1844 and later by Emden (1926) and Eisner (1967).
The decisive factor is the earth's orbital speed around the sun of around 30 km / s, which means that in 6 months there is a maximum speed difference of around 60 km / s. As a result, the fixed star sky is in motion from the perspective of the earth as a whole . Now it is not possible for the terrestrial observer to decide from a single measurement whether the ray arrives at him inclined because there is an aberration effect, or whether the ray was emitted inclined from a star that rests in the same inertial system as the observer . It is therefore necessary to carry out a second measurement at a later point in time , which is compared with the first measurement. The annual change in the aberration angle measured in this way corresponds (neglecting minor effects such as parallax ) to the result of the relativistic aberration formula, whereby the speed used is not the relative speed between the star and the earth, but the relative speed between the inertial system in which the earth rests while the first measurement, and the inertial system in which it rests in the subsequent measurement as it orbits the sun.
Derivation
In classical mechanics , the speed components of a ray in different inertial systems are linked by the Galileo transformation . A beam that propagates exclusively in the y-direction in an inertial system receives the speed component in the x-direction in addition , in a second inertial system that is relatively moving , while the component in the y-direction remains the same. The aberration formula results from:
- .
This result is only valid as an approximation, because as Albert Einstein showed in 1905, according to the special theory of relativity, the Lorentz transformation or the relativistic addition of speed must be applied. This results in speed components in the x-direction and in the y-direction, whereby the overall speed of the jet remains the same . The correct, relativistic aberration formula for this special case is thus:
where the Lorentz factor is. The deviation from the classical formula is very small at low speeds (compared to the speed of light). The same result is obtained if one takes into account that light rays or photons have a momentum of (where is the energy). Here, too, a transformation into a relatively moving system results in a corresponding change in the pulse components in accordance with the relativistic aberration formula.
In the event that the beam is inclined in both systems, the general aberration formula applies, which can be given in some equivalent variants (the first variant comes from Einstein 1905):
- ,
if the angle is in the first system and in a moving system.
history
The aberration was discovered in 1725 by the English astronomer James Bradley (and independently a little later by Eustachio Manfredi in Italy). He actually wanted to measure the annual parallax of the star Etamin in order to finally get an idea of the distances between the stars. But he would not have been able to prove the parallax (far below 0.1 ″) with the means of the 18th century; this only succeeded in 1838 Friedrich Wilhelm Bessel with a closer star. The displacement observed by Bradley could not be parallax because it was transverse to the direction expected for parallax. Bradley, however, was able to interpret the observed displacement on the basis of Isaac Newton's corpuscle theory or emission theory by a simple addition of the velocities. While this aberration formula was largely correct in vacuum, it contradicted the experiment by François Arago (1810) who used a prism to measure deviations from normal aberration. According to emission theory, a different angle should have followed due to different speeds of light, but no such effect was measured. Above all, however, the emission theory predicts a source dependence of the longitudinal speed of light, which has been repeatedly refuted experimentally, whereby the emission theory has to be rejected (see corpuscle theory).
In the 19th century this explanation was replaced by the assumption that light is not a particle, but a wave transmitted in the ether . The aberration (and later the Fizeau experiment ) played an important role in the question of the relative movement between matter and aether, because it spoke against a complete entrainment of the aether through matter, and seemed to confirm the existence of a stationary or immobile aether. But also this explanation had the problem that the wave planes of the wave fronts in the ether should not be subject to any aberration. Therefore one had to fall back on the concept of energy transfer according to the Poynting vector , which determines the beam path. An analogous explanation offered itself when it was recognized that the wave packets were “cut out” of the wave fronts in the telescope by interference, whereby the aberration could be applied to the wave packets. In addition, the theory of the aether at rest also contradicts Arago's zero result , since in media there would have to be deviations from the usual aberration due to the relative movement earth-ether (“ether wind”). However, Augustin Jean Fresnel was able to solve this problem by assuming that the ether is partly carried by the matter according to Fresnel's entrainment coefficient . While this model was mathematically successful, the assumption of aether entrainment (and alternative entrainment models as by George Gabriel Stokes ) was very problematic and could never be carried out consistently. Ultimately, the idea of an ether as a carrier medium for light had to be rejected because its state of motion could not be measured (see Michelson-Morley experiment ).
These explanations were eventually replaced and simplified significantly in the context of special relativity . Here it is irrelevant whether light is perceived as a wave or a particle, because the wave fronts are also "tilted" for an observer resting on earth due to the relativity of simultaneity and thus easily result in the aberration of the light. Similarly, the inclination of the photon trajectory is calculated by the relativistic addition of the velocities . Albert Einstein wrote in 1952 that his direct path to special relativity (SRT) was determined by electromagnetic induction , but also by the aberration of light and the Fizeau experiment . And Robert S. Shankland reports on a conversation with Einstein:
“He continued to say the experimental results which had influenced him most were the observations of stellar aberration and Fizeau's measurements on the speed of light in moving water. "They were enough," he said. "
“He [Einstein] went on to say that the experimental results that influenced him most were observations of stellar aberration and Fizeau's measurements of the speed of light in moving water. 'These were sufficient,' he said. "
See also
Individual evidence
- ^ A b US Nautical Almanac Office: Astronomical Almanac . United States Government Printing Office , 2008, ISBN 0118873423 , p. M-1.
- ↑ a b c Max Born : Einstein's theory of relativity . Springer, Berlin / Heidelberg / New York 2003, ISBN 3-540-00470-X .
- ↑ a b c d Liebscher, D.-E .; Brosche, P .: Aberration and relativity . In: Astronomical News . 319, No. 5, 1998, p. 309. bibcode : 1998AN .... 319..309L . See also: Pitfalls in aberration (PDF; 527 kB)
- ↑ Herschel, John Frederick William: Letter from the Baronet Herschel to the editor . In: Astronomical News . 22, No. 520, 1844, pp. 249-254. bibcode : 1844AN ..... 22..249H .
- ↑ Emden, R .: Aberration and Theory of Relativity . In: The natural sciences . 14, No. 16, 1926, pp. 329-335. doi : 10.1007 / BF01506966 .
- ↑ Eisner, Edward: Aberration of Light from Binary Stars-a Paradox? . In: American Journal of Physics . 35, No. 9, 1967, pp. 817-819. doi : 10.1119 / 1.1974259 .
- ↑ RK Pathria: The theory of relativity . Courier Dover Publication, 2003, ISBN 0486428192 , pp. 113-114.
- ^ " My own thought was more indirectly influenced by the famous Michelson-Morley experiment. I learned of it through Lorentz 'path breaking investigation on the electrodynamics of moving bodies (1895), of which I knew before the establishment of the special theory of relativity Lorentz 'basic assumption of a resting ether did not seem directly convincing to me, since it led to an [struck out: to me artificial appearing] interpretation of the Michelson-Morley experiment, which [struck out: did not convince me] seemed unnatural to me. My direct path to the sp. th. rel. was mainly determined by the conviction that the electromotive force induced in a conductor moving in a magnetic field is nothing other than an electric field. But the result of Fizeau's experiment and the phenomenon of aberration also guided me "; Norton, John D .: Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905 . In: Archive for History of Exact Sciences . 59, 2004, pp. 45-105. bibcode : 2004AHES ... 59 ... 45N . doi : 10.1007 / s00407-004-0085-6 .
- ^ RS Shankland: Conversations with Albert Einstein . In: American Journal of Physics . 31, No. 1, 1963, pp. 47-57. bibcode : 1963AmJPh..31 ... 47S . doi : 10.1119 / 1.1969236 .