Born coordinates

Fig. 1: The space-time of the Born coordinates in Minkowski space (cylinder coordinates). The red lines ( | ) are the world lines of the points at rest on the rotating disk. The alternating gray and blue stripes show areas with constant time . The orange lines ( / \ ) show light-like curves with constant and . ${\displaystyle T}$ ${\displaystyle R,\,T}$ ${\displaystyle \Phi }$

The Born coordinates describe in relativistic physics , a map for a part of the flat Minkowski-space of the special theory of relativity , the spatial cylinder with the corresponding line element with the signature , so the natural units and the angular velocity is ${\displaystyle r<1/\omega .}$ ${\displaystyle (1,3)}$ ${\displaystyle (+,-,-,-),}$ ${\displaystyle G=c=1}$ ${\displaystyle \omega }$

${\displaystyle \mathrm {d} s^{2}=\left(1-\omega ^{2}r^{2}\right)\mathrm {d} t^{2}-2\,\omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <t{,}\,z<\infty {,}\quad 0<r<1/\omega {,}\quad -\pi \leq \phi <\pi .}$

The Born coordinates are used for the mathematical analysis of physics by so-called Langevin observers who rest on a ring at a constant distance from the center of rotation of rotating rigid disks (see Ehrenfest's paradox ). These coordinates were first described in connection with Max Born's (1909) relativistic physics of rigid bodies , which was further developed for rotating bodies by Gustav Herglotz (1909) among others . For a general overview of accelerations in the Minkowski space-time, see Acceleration (Special Theory of Relativity) .

Clock synchronization and distance measurement

Fig. 2: The animation shows the synchronization of the clocks at , and on the ring with the radius and about 62% of the speed of light on a rotating disk with the central clock in the center of rotation as a reference. The thus synchronized clocks , , and show the coordinates time of the inertial system in Minkowski space in which the rotational axis of the disc rests. The dotted lines show the path of the light rays (zero geodesics) in the inertial system. The colored lines represent the corresponding zero geodesics in the reference system of the rotating disk. The green lines are the ending radial zero geodesics. They are bent in the direction of rotation. The blue lines are the incoming radial zero data. They are bent against the direction of rotation. It should be noted that outgoing and incoming radial null data do not take the same route. The violet curve shows the outwardly curved null geodesic from to , the red curve, the inwardly curved null geodesic from to . The light rays emitted with and at the same time (with respect to the inertial system) do not arrive at the Langevin observer at the same time . For this the clocks and are not synchronous. ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle r=1}$ ${\displaystyle {\rm {O}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {O}}}$ ${\displaystyle t}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$

Ideal clocks at rest on the rotating disk cannot be synchronized without contradictions. Not on a ring with a constant diameter on which the clocks run at least at the same speed, and certainly not on the whole disc, on which the clocks run by the factor slower the further they are from the axis of rotation ( time dilation ). This means that the clocks do not run at the same speed along a radius , but rather become slower with increasing compared to a reference clock in the center of rotation . ${\displaystyle \gamma ^{-1}=(1-\omega {^{2}}r{^{2}})}$ ${\displaystyle t=\phi =z={\rm {const.}}}$ ${\displaystyle r=0}$ ${\displaystyle r>0}$

Since the Born coordinates describe part of the flat Minkowski space, the clocks can be synchronized as there, by using the clock in the center of rotation (clock in the center of rotation) as a reference and z. B. sends out a light signal every second, with which all clocks on the rotating disk are synchronized (see Fig. 2). The receiver clocks , and know the respective transit time of the signal from the center of rotation and adjust their time accordingly. This means that all observers who are on the axis of rotation, light signals from the clocks on the disk in seconds be sent tact, are received by the second. If the signals from clocks are sent on a ring with a constant radius, they are also received at the same time . In such a synchronized, the clocks in , , and in synchronism with the time coordinates of the inertial system, in which the rotational axis of the rotating disk rests. ${\displaystyle {\rm {O}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {O}}}$ ${\displaystyle t}$

However , the situation is unsatisfactory for the Langevin observer (watch ). Two problems arise for him. First, his clock synchronized in this way runs too fast compared to a clock that he has calibrated to the standard SI second . Second, he makes the irritating observation that two light signals that are emitted simultaneously by the two equally distant clocks and on his ring do not reach him at the same time . Since he knows that the clocks and are equidistant from his watch , there are only two options. Either the light propagation is not isotropic - light from in the direction of rotation is with him earlier (the speed of light would therefore be faster than ) than light from opposite to the direction of rotation (the speed of light would therefore be slower than ). Or the clocks and are out of sync with his clock . ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle c}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle c}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$

To synchronize them from his point of view, he proceeds as in the inertial system. He calibrates the clock , and the SI second and synchronizes the clocks , and with his watch by Einstein Synchronization (an internal synchronization ). He realizes that he has to reset the clock that is in the direction of rotation and that he has to advance the clock that is opposite to the direction of rotation. Two light signals now simultaneously from and are sent out to meet simultaneously in one (but they meet not simultaneously at the clock on). If you synchronize all clocks along the ring in this way, another problem arises. At least two adjacent clocks do not show the same time. In total, the clocks show a time difference along the ring with the radius r . ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {A}}}$ ${\displaystyle {\rm {B}}}$ ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {O}}}$ ${\displaystyle \Delta t=(2\pi \omega r^{2})/(1-\omega ^{2}r^{2})}$

In addition, the Langevin observer notes that no matter how he measures the distances of his local environment, the geometry is non-Euclidean and is best described by a Riemannian metric, the so-called Langevin-Landau-Lifschitz metric. This metric, in turn, is very well approximated by the metric of the hyperbolic level. When measuring large distances beyond the local environment, the results depend on the measuring method, which cannot be described with the properties of a Riemann metric. The long distances measured with the radar method are not even symmetrical. The measured distance from to is not equal to the measured distance from to . This means that the geometry of the rotating disk is neither a Euclidean nor a Riemannian geometry. ${\displaystyle {\rm {L}}}$ ${\displaystyle {\rm {O}}}$ ${\displaystyle {\rm {O}}}$ ${\displaystyle {\rm {L}}}$

The rotating disk is not a paradox. No matter which method the Langevin observer uses to analyze his local environment: he determines that he is in a rotating frame of reference and not in an inertial frame.

Langevin observer in cylindrical coordinates

For the derivation of the Born coordinates, it makes sense to first display the Langevin observers in cylindrical coordinates . Their world lines form a time-like congruence that can be viewed as rigid , since the corresponding expansion tensor vanishes (see below). The Langevin observers rotate around the cylinder's axis of symmetry.

Fig. 3: Representation of the helical world line of a Langevin observer in cylindrical coordinates (red curve). Also shown are the future light cones (gold-colored) and the tetrads (base vectors) of the local reference systems (black vectors). The gray cylinder is a surface with constant and the green dashed line is the axis of symmetry (axis of rotation) at . The blue curve is an integral curve of the azimuthal vector . The coordinate is not essential for this illustration and is omitted. ${\displaystyle R}$ ${\displaystyle R=0}$ ${\displaystyle {\vec {p}}_{3}}$ ${\displaystyle Z}$

From the line element of the Minkowski space in cylindrical coordinates

${\displaystyle {\begin{aligned}&\mathrm {d} s^{2}=\mathrm {d} T^{2}-\mathrm {d} Z^{2}-\mathrm {d} R^{2}-R^{2}\,\mathrm {d} \Phi ^{2},\;\;\\&-\infty <T,\;Z<\infty ,\quad 0<R<\infty ,\quad -\pi \leq \Phi <\pi ,\end{aligned}}}$

the tetrads (vector fields of the basis vectors) of the local reference system for stationary observers can be read directly:

${\displaystyle {\vec {e}}_{0}=\partial _{T},\;\;{\vec {e}}_{1}=\partial _{Z},\;\;{\vec {e}}_{2}=\partial _{R},\;\;{\vec {e}}_{3}={\frac {1}{R}}\,\partial _{\Phi }.}$

${\displaystyle {\vec {e}}_{0}}$is a time-like vector field. , and are space-like vector fields. ${\displaystyle {\vec {e}}_{1}}$ ${\displaystyle {\vec {e}}_{2}}$ ${\displaystyle {\vec {e}}_{3}}$

With a Lorentz boost of the vector fields of the basis vectors with in the direction (application of the Lorentz transformation to and ), the vector fields of the basis vectors result for the Langevin observer with ${\displaystyle \omega R}$ ${\displaystyle {\vec {e}}_{3}}$ ${\displaystyle {\vec {e}}_{3}}$ ${\displaystyle {\vec {e}}_{0}}$

${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\partial _{\Phi },}$

${\displaystyle {\vec {p}}_{1}=\partial _{Z},\;\;{\vec {p}}_{2}=\partial _{R},}$

${\displaystyle {\vec {p}}_{3}={\frac {1}{\sqrt {1-\omega ^{2}\,R^{2}}}}\;{\frac {1}{R}}\,\partial _{\Phi }+{\frac {\omega \,R}{\sqrt {1-\omega ^{2}\,R^{2}}}}\,\partial _{T}.}$

These vector fields were first used (implicitly) by Paul Langevin in 1935. Thomas A. Weber did not provide a detailed description until 1997. In contrast to the cylindrical coordinates, these vector fields are defined in the area . This limitation is fundamental because the speed of Langevin observers is approaching the speed limit of the speed of light. ${\displaystyle 0<R<\infty }$ ${\displaystyle 0<R<1/\omega }$ ${\displaystyle R\rightarrow 1/\omega }$

Fig. 4: Representation of the world lines (dashed blue curves) of the neighboring observers to a certain Langevin observer (red helical curve). From the point of view of a particular Langevin observer. The cyan curve represents the movement of the radial vector field (the radial base vector) for a quarter of a full revolution around the axis of rotation (green curve). ${\displaystyle {\vec {p}}_{2}}$

Each integral curve of the time-like vector field is mapped in cylindrical coordinates as a helical curve with a constant radius (see the red curves in Fig. 1 and Fig. 3) and represents a Langevin observer at rest with respect to the rotating disk. Additional Langevin observers, who are on a ring with the radius and the angular velocity with the first , should be simultaneously (synchronous) on the integral curve of the vector field (see the blue curve in Fig. 3) . However, it turns out that ideal clocks cannot be synchronized along the blue curve using Einstein synchronization, since the blue curve intersects the red curve at different points. At least two neighboring clocks show different times, because the blue curve is simultaneous , but two different points on the red curve have a time difference - the blue curve is not a closed curve in space-time and the neighboring clocks are not synchronous. This is the first indication that no satisfactory description of a spatial geometry can be found for the rotating disk on which all events are simultaneous. Neither for the whole rotating disk nor for a rotating ring with a radius  . ${\displaystyle {\vec {p}}_{0}}$ ${\displaystyle R}$ ${\displaystyle \omega }$ ${\displaystyle {\vec {p}}_{3}}$ ${\displaystyle R}$

In contrast, the projection of the helical world line of a Langevin observer onto the spatial hyperplane is a circle - i.e. a closed curve in space-time. In addition, the vector field of the basis vectors is a space-like killing vector field , the integral curves of which are closed curves in space (de-facto circles). They degenerate into curves with zero length. This corresponds to the idea of ​​cylindrical symmetry and the idea of ​​a rotating Langevin observer. However, this notion based on cannot be realized because the ideal clocks on the ring cannot be synchronized without contradictions and therefore (simultaneity) does not make sense if the clocks cannot be clearly synchronized. ${\displaystyle T=\mathrm {const.} }$ ${\displaystyle {\vec {e}}_{3}=(1/R)\,\partial _{\Phi }}$ ${\displaystyle R=0}$ ${\displaystyle T=\mathrm {const.} }$ ${\displaystyle T=\mathrm {const.} }$

The four acceleration of the time-like vector field is ${\displaystyle {\vec {p}}_{0}}$

${\displaystyle \nabla _{{\vec {p}}_{0}}{\vec {p}}_{0}={\frac {-\omega ^{2}\,R}{1-\omega ^{2}\,R^{2}}}\;{\vec {p}}_{2}.}$

It points radially to the axis of rotation and depends only on the constant radius and the constant angular velocity of the helical world line of the Langevin observer ( centripetal acceleration ). With the kinematic decomposition (see four acceleration above) the expansion tensor and the vortex vector result . The expansion tensor is zero. This means that the distances of the Langevin observers to each other and to the axis of rotation remain constant ( rigid disc). The vortex vector results from ${\displaystyle R}$ ${\displaystyle \omega }$

${\displaystyle {\vec {\Omega }}={\frac {\omega }{1-\omega ^{2}\,R^{2}}}\;{\vec {p}}_{1}}$

and is parallel to the axis of rotation. This means that the Langevin observers rotate around the axis of rotation. But that also means that the Langevin observers rotate around their own axis. This corresponds to the idea of ​​a local turbulence . In Fig. 4, the cyan-colored curve shows how the space-like vector fields wind around the vector field ( - the -coordinate - is replaced by - the time - in Fig. 4 , since the -coordinate is irrelevant here). The local reference systems of the Langevin observers also rotate and are not inertial systems and theirs are aligned with the radial basis vector . This local rotation from and around the axis can be canceled by a constant local counter-rotation. ${\displaystyle {\vec {p}}_{2},\;{\vec {p}}_{3}}$ ${\displaystyle {\vec {p}}_{1}}$ ${\displaystyle {\vec {p}}_{1}}$ ${\displaystyle Z}$ ${\displaystyle {\vec {e}}_{0}}$ ${\displaystyle Z}$ ${\displaystyle {\vec {p}}_{2}=\partial _{R}}$ ${\displaystyle {\vec {e}}_{2}=\partial _{R}}$ ${\displaystyle {\vec {p}}_{2}}$ ${\displaystyle {\vec {p}}_{3}}$ ${\displaystyle {\vec {p}}_{1}}$

Transformation in Born coordinates

Fig. 5: Representation of an idea of ​​a “space at a certain time” in Born coordinates (a “simultaneity surface” or a three-dimensional hypersurface). The area shows the area with the angular velocity. Starting from the radial ray with (the blue line at the back right), the area is formed by the integral curves with the tangent vector . However, this notion of “space at a specific time” is doomed to failure for at least two reasons. First, the vectors would have to be tangent vectors of this “simultaneity surface”, but it is only tangential for (with the base point on the blue line). Second, the “simultaneity surface” has a discontinuity (a “jump”, see the blue grid lines). No clear time can be defined on this discontinuity. ${\displaystyle 0<r<1}$ ${\displaystyle \omega =1/5.}$ ${\displaystyle \phi =0}$ ${\displaystyle {\vec {p}}_{3}}$ ${\displaystyle {\vec {p}}_{1},\,{\vec {p}}_{2},\,{\vec {p}}_{3}}$ ${\displaystyle {\vec {p}}_{2}=\partial _{r}}$ ${\displaystyle \phi =0}$ ${\displaystyle \phi =\pi }$

To obtain the Born coordinates, the helical world lines of the Langevin observers are transformed using the transformation

${\displaystyle t=T,\;\;z=Z,\;\;r=R,\;\;\phi =\Phi -\omega \,T}$

"Stretched" and the new line element results

${\displaystyle \mathrm {d} s^{2}=\left(1-\omega ^{2}r^{2}\right)\mathrm {d} t^{2}-2\,\omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <t,\,z<\infty ,\quad 0<r<{\frac {1}{\omega }},\quad -\pi <\phi <\pi .}$

Because of the mixed term , the Born coordinates are not an orthogonal coordinate system . ${\displaystyle \omega \,r^{2}\mathrm {d} t\,\mathrm {d} \phi }$

The world lines of the Langevin observers are now straight vertical lines. In Born coordinates the vector fields are the base vectors of the Langevin observer

${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t},}$

${\displaystyle {\vec {p}}_{1}=\partial _{z},\;\;{\vec {p}}_{2}=\partial _{r},}$

${\displaystyle {\vec {p}}_{3}={\frac {\sqrt {1-\omega ^{2}\,r^{2}}}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}.}$

The helical world lines of the Langevin observers in cylindrical coordinates are straight lines in Born coordinates. However, the straight world lines of the static observer in cylindrical coordinates that rest next to the rotating disk are helical world lines in Born coordinates. In contrast to the cylindrical coordinates , not only the vector fields of the base vectors of the Langevin observer are limited to the area , but the Born coordinates as a whole. ${\displaystyle 0<r<1/\omega }$

The kinematic decomposition of the time-like congruence delivers the same results as before, but with the new Born coordinates. The acceleration vector is ${\displaystyle {\vec {p}}_{0}={\frac {1}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t}}$

${\displaystyle \nabla _{{\vec {p}}_{0}}\,{\vec {p}}_{0}={\frac {-\omega ^{2}\,r}{1-\omega ^{2}\,r^{2}}}\,{\vec {p}}_{2},}$

the expansion tensor is zero and the vortex vector is

${\displaystyle {\vec {\Omega }}={\frac {\omega }{1-\omega ^{2}\,r^{2}}}\;{\vec {p}}_{1}.}$

The co-vector field, which is dual to a time-like unit vector field, defines an infinitesimal spatial hyperplane in each local reference system. Whether these infinitesimal spatial hyperplanes can be connected to form a global spatial hyperplane that is orthogonal to the congruence of the world lines everywhere is determined by the condition for complete integrability . It turns out that this condition is fulfilled if and only if the vortex tensor is zero. For the static observer in cylindrical coordinates there exist such spatial hypersurfaces for which applies, but not for the Langevin observer. In particular, the spatial hypersurfaces in Born coordinates are orthogonal to the world lines of the static observer, not to the world lines of the Langevin observer. ${\displaystyle T=\mathrm {const.} }$ ${\displaystyle t=\mathrm {const.} }$

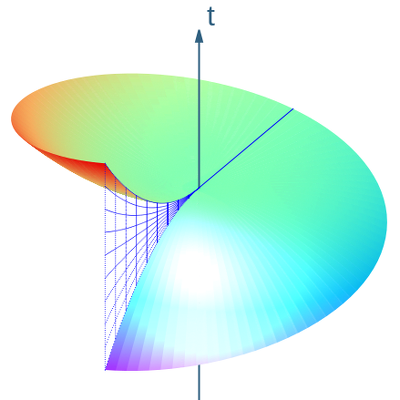
This becomes clear when the integral curves of the Langevin vector field

${\displaystyle {\vec {p}}_{3}={\sqrt {1-\omega ^{2}\,r^{2}}}\,{\frac {1}{r}}\,\partial _{\phi }+{\frac {\omega \,r}{\sqrt {1-\omega ^{2}\,r^{2}}}}\,\partial _{t},}$

running through the radius . These curves lie in the surface ${\displaystyle \phi =0,\,t=0}$

${\displaystyle \phi +\omega \,t-{\frac {t}{\omega \,r^{2}}}=0,\;\;-\pi <\phi <\pi }$

(see Fig. 5). The coordinate that is not essential for the display has been replaced by the coordinate . It makes sense to interpret this area as a spatial “simultaneity area” for Langevin observers. This is not possible for two reasons. First, the condition for complete integrability is not fulfilled, so that there is no spatial hypersurface to which the vector fields are tangent. The vector field is only for tangential. This is an infinitesimal (local) problem. Second, it can be seen in Fig. 5 that the spatial hyperplane constructed in this way has a discontinuity , a jump (see the blue grid lines in Fig. 5). This is a global problem and a consequence of the fact that the clocks of the Langevin observers cannot be synchronized consistently. Neither on the whole rotating disk nor on a ring with constant . ${\displaystyle z}$ ${\displaystyle t}$ ${\displaystyle {\vec {p}}_{2},\,{\vec {p}}_{3}}$ ${\displaystyle {\vec {p}}_{2}}$ ${\displaystyle \phi =0}$ ${\displaystyle r}$

Zero geodesics

Fig. 6: In cylindrical coordinates, the zero geodesics are straight lines (green curve). In parametric representation with the affine parameter λ are the radius and the angle . ${\displaystyle R={\sqrt {\lambda ^{2}(E^{2}-P^{2})+R_{\mathrm {min} }^{2}}}}$ ${\displaystyle \Phi =\Phi _{0}+\operatorname {arctan} \left[(\lambda {\sqrt {E^{2}-P^{2}}})/(R_{\mathrm {min} }\,\operatorname {sgn} {(L)})\right]}$

The zero geodesics in cylinder coordinates result from the geodesic equations

${\displaystyle {\ddot {T}}=0,\;\;{\ddot {Z}}=0,\;\;{\ddot {R}}-R\,{\dot {\Phi }}^{2}=0,\;\;{\ddot {\Phi }}+{\frac {2}{R}}\,{\dot {\Phi }}\,{\dot {R}}=0.}$

The first integrals for can be given directly with ${\displaystyle {\ddot {T}},\,{\ddot {Z}},\,{\ddot {\Phi }}}$

${\displaystyle {\dot {T}}=E,\;\;{\dot {Z}}=P,\;\;{\dot {\Phi }}={\frac {L}{R^{2}}}.}$

If this is used in the expression for the line element of the cylindrical coordinates and is also set (for the zero geodesics), the result is ${\displaystyle \mathrm {d} s^{2}=0}$

${\displaystyle {\dot {R}}^{2}=E^{2}-P^{2}-{\frac {L^{2}}{R^{2}}}\geq 0.}$

This results in a zero geodesic for the minimum radius R _min

${\displaystyle E^{2}-P^{2}-{\frac {L^{2}}{R_{\mathrm {min} }^{2}}}=0\quad }$ so ${\displaystyle \quad R_{\mathrm {min} }={\frac {|L|}{\sqrt {E^{2}-P^{2}}}}}$

and further

${\displaystyle {\dot {R}}^{2}=L^{2}\left({\frac {1}{R_{\mathrm {min} }^{2}}}-{\frac {1}{R^{2}}}\right).}$

This is also found for the first integral. ${\displaystyle {\ddot {R}}}$

Fig. 7: Radial zero geodesics in Born coordinates are shown on the left. The green curve shows an outgoing light beam, the red curve an incoming light beam. The counterclockwise rotating Langevin observers sit on the blue ring with R = R ₀ .
• The parameters for these curves are: ω = +0.2, R ₀ = r ₀ = 1.

On the right-hand side, zero geodesics in Born coordinates between two Langevin observers are shown on the ring r = r ₀ = 1. Zero geodesics in the direction of rotation (counterclockwise - green curve) are bent inwards, zero geodesics against the direction of rotation (clockwise - red curve) are bent outwards. The proper time for the Langevin observer Δ t ₁₂ that the light beam needs from L ₁ to L ₂ is 1.311, the proper time Δ t ₂₁ from L ₂ to L ₁ is 1.510. These two times are not identical (asymmetrical for the observer L ₁ L ₂ ), but the radar distance (Δ t ₁₂ + Δ t ₂₁ ) / 2 is. For ω → 0, both times Δ t ₁₂ and Δ t ₂₁ approach √2 = 1.414.
• The parameters for these curves and the next are: ω = +0.1, R ₀ = r ₀ = 1, Δ ϕ (L ₁ , L ₂ ) = π / 2, Δ ϕ (L ₁ , L ₃ ) = π

In the middle one can see zero geodesics between opposite Langevin observers L ₁ and L ₃ (gray curves), which bend symmetrically around the center of rotation.

The solution of the zero geodesics as curves with the affine parameter λ is (see Fig. 6)

${\displaystyle {\begin{aligned}R&={\sqrt {(E^{2}-P^{2})\,\lambda ^{2}+L^{2}/(E^{2}-P^{2})}}=\\&={\sqrt {(E^{2}-P^{2})\,\lambda ^{2}+R_{\mathrm {min} }^{2}}},\\T&=T_{0}+E\,\lambda ,\\[1em]Z&=Z_{0}+P\,\lambda ,\\\Phi &=\Phi _{0}+\operatorname {arctan} \left({\frac {E^{2}-P^{2}}{L}}\,\lambda \right)=\\&=\Phi _{0}+\operatorname {arctan} \left({\frac {\sqrt {E^{2}-P^{2}}}{R_{\mathrm {min} }\,\operatorname {sgn} {(L)}}}\,\lambda \right).\end{aligned}}}$

The trajectories of the zero geodesics, ie the traces of their “projection” into the spatial hyperplane, are of course straight lines in Minkowski space with cylindrical coordinates and given by ${\displaystyle T=\mathrm {const.} }$

${\displaystyle R={\frac {R_{\mathrm {min} }}{\cos(\Phi -\Phi _{0})}}.}$

For radial zero geodesics is . In addition, when inserted into the equations above, the following applies to outgoing radial zero geodesics ${\displaystyle R_{\mathrm {min} }=0}$ ${\displaystyle E=1,\,P=0}$

${\displaystyle T=\lambda ,\;Z=Z_{0},\;R=\lambda ,}$

${\displaystyle \Phi =\mathrm {const.} =\omega \,R_{0}.}$

${\displaystyle R_{0}}$is the distance of the Langevin observer from the center of rotation (see Fig. 7). If these equations are transformed into Born coordinates, the result is for the outgoing light beam

${\displaystyle r=r_{0}-{\frac {\phi }{\omega }}.}$

In Born coordinates, this trajectory is not a straight line (see the green curve in Fig. 7). As shown in the section Transformation in Born coordinates , in Born coordinates these trajectories are strictly speaking not a projection into a spatial hyperplane, as such is not defined for (see Fig. 5). ${\displaystyle t=\mathrm {const.} }$

For incoming radial zero geodesics this results

${\displaystyle r={\frac {\phi }{\omega }}}$

shown as a red curve in Fig. 7.

In order to send a laser pulse to the stationary observer S at r = 0, the Langevine observer must aim ahead at r = R ₀ (for him, S moves counterclockwise from right to left). The same applies to the observer S who wants to send a laser pulse to the observer L. For ω > 0 the incoming and outgoing zero geodesics are different curves in space-time with different trajectories.

Null geodesics between Langevin observers on the ring with r = R ₀ are also bent inwards or outwards for ω > 0. To see this, the equations for the zero geodesics running in the direction of rotation are in cylindrical coordinates in the form

${\displaystyle T=R_{\mathrm {min} }\,\tan(\Phi ),}$

${\displaystyle R={\frac {R_{\mathrm {min} }}{\cos(\Phi )}}}$

written. The transformation in Born coordinates results in

${\displaystyle t=r_{\mathrm {min} }\,\tan(\phi +\omega \,t),}$

${\displaystyle r={\frac {r_{\mathrm {min} }}{\cos(\phi +\omega \,t)}}}$

or solved for r and ϕ

${\displaystyle r={\sqrt {r_{\mathrm {min} }^{2}+t^{2}}},}$

${\displaystyle \phi =-\omega \,t+\operatorname {arctan} (t/r_{\mathrm {min} }).}$

This trajectory is actually bent inwards for ω > 0 (see the green curve in Fig. 7). The curves result for zero geodesics against the direction of rotation (see the red curve in Fig. 7)

${\displaystyle r={\sqrt {r_{\mathrm {min} }^{2}+t^{2}}},}$

${\displaystyle \phi =-\omega \,t-\operatorname {arctan} (t/r_{\mathrm {min} })}$

whose trajectories are bent outwards. For the Langevin observers, it applies that they have to hold up in order to send laser pulses .

This concludes the considerations on zero geodesics, because a zero geodesy is either radial or has a minimum radius r _min .

Radar distance on a large scale

Fig. 8: Zero geodesics (laser pulses) moving back and forth in Born coordinates between the two Langevin observers A and B on the rotating ring with the radius r ₀ and the angular velocity ω . The green curve shows the zero geodesics for the impulse running against the direction of rotation, the red curve for the impulse running in the direction of rotation. The transit time (proper time) from A to B Δ τ _AB is smaller than the transit time from B to A Δ τ _BA . The radar distance (Δ τ _AB + Δ τ _AB ) / 2 of B for A is identical to the radar distance of A for B.

For accelerated observers, even in the simplest case of the flat Minkowski space, there are various options for distance measurement that prove to be operationally useful. Of these, the radar distance is the simplest. If a stationary observer C in the center of rotation of the disk R = r = 0 measures the transit time to a Langevin observer A on a ring with the radius , he receives the result . For Langevin observer A, the situation is different. It measures a slightly shorter running time, since its clock is time-dilated by the factor compared to the clock of the stationary observer C. He receives as a result of his measurement . Even this simple case is difficult. Observers A and C do not agree on their distance. The radar measurement does not provide a symmetrical result. ${\displaystyle r_{0}}$ ${\displaystyle r_{0}}$ ${\displaystyle {\sqrt {1-\omega ^{2}r_{0}^{2}}}}$ ${\displaystyle r_{0}{\sqrt {1-\omega ^{2}r_{0}^{2}}}}$

In comparison, the radar measurement between two Langevin observers A and B on the ring with the radius gives a symmetrical result. The observer A measures the distance to B in the same way as the observer B measures the distance to A (see Fig. 9). The transit times between A and B can be determined using the equations for the general zero geodesics . With the angle ΔΦ between A and B, the running time Δ t _AB (in coordinate time) from A to B results ${\displaystyle r_{0}}$

${\displaystyle \Delta \phi =+\omega \,\Delta t_{AB}+2\operatorname {arctan} \left(\Delta t_{AB}/{\sqrt {4r_{0}^{2}-\Delta t_{AB}^{2}}}\right)}$

and for the running time Δ t _BA (in coordinate time) from B to A.

${\displaystyle \Delta \phi =-\omega \,\Delta t_{BA}+2\operatorname {arctan} \left(\Delta t_{BA}/{\sqrt {4r_{0}^{2}-\Delta t_{BA}^{2}}}\right).}$

The two transit times can be calculated numerically with these non-linear equations. The radar distance taking into account the time dilation is thus

${\displaystyle l={\sqrt {1-\omega ^{2}r^{2}}}\;{\frac {\Delta t_{AB}+\Delta t_{BA}}{2}}.}$

In spite of the difficulties presented in determining large radar distances, for example, Märzke-Wheeler coordinates can be used to construct a simultaneity surface for a specific Langevin observer, with the aid of which large radar distances can be measured.

Radar distance on a small scale

As shown in the Transformation in Born Coordinates section, Born coordinates cannot be used to define "simultaneity surfaces". However, the time-like congruence of the Langevin observers is stationary and their world lines can be replaced by points. As a result, a quotient space of the area of the Minkowski space is formed. This space is a three-dimensional topological manifold , which can be converted into a three-dimensional Riemannian manifold by means of a Riemannian metric , with which operational distances can easily be found. ${\displaystyle 0<R<1/\omega }$

The starting point is the line element in Born coordinates

${\displaystyle \mathrm {d} s^{2}=(1-\omega ^{2}\,r^{2})\,\mathrm {d} t^{2}-2\,\omega \,r^{2}\,\mathrm {d} t\,\mathrm {d} \phi -\mathrm {d} z^{2}-\mathrm {d} r^{2}-r^{2}\,\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <t,z<\infty ,\;\;0<r<{\frac {1}{\omega }},\;\;-\pi <\phi <\pi .}$

If it is set and then resolved, the light transit times there and back result ${\displaystyle \mathrm {d} s^{2}=0}$ ${\displaystyle \mathrm {d} t}$

${\displaystyle \mathrm {d} t_{+}={\frac {\omega \,r^{2}\,\mathrm {d} \phi +{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}},}$

${\displaystyle \mathrm {d} t_{-}={\frac {\omega \,r^{2}\,\mathrm {d} \phi -{\sqrt {(1-\omega ^{2}\,r^{2})\;(\mathrm {d} z^{2}+\mathrm {d} r^{2})+r^{2}\,\mathrm {d} \phi ^{2}}}}{1-\omega ^{2}\,r^{2}}}.}$

And thus the local (infinitesimal) radar distance as the arithmetic mean of the light travel time

${\displaystyle {\sqrt {1-\omega ^{2}\,r^{2}}}\;{\frac {\mathrm {d} t_{+}-\mathrm {d} t_{-}}{2}}={\sqrt {\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}}}}.}$

Thus the quotient space has the Riemann line element

${\displaystyle \mathrm {d} \sigma ^{2}=\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {r^{2}\,\mathrm {d} \phi ^{2}}{1-\omega ^{2}\,r^{2}}},}$

${\displaystyle -\infty <z<\infty ,\;\;0<r<{\frac {1}{\omega }},\;\;-\pi <\phi <\pi }$

which corresponds to the distance between two neighboring Langevin observers with an infinitesimal distance. This metric is called the Langevin-Landau-Lifschitz metric and represents the "small radar distance". This metric was introduced by Langevin and generalized by Lifschitz and Landau as "small radar distance" for quotient spaces of Lorentz manifolds formed by any stationary time-like congruences.

For the quotient space of the Langevin-Landau-Lifschitz metric, the calculated Krümmungsskalar with

${\displaystyle {R}={\frac {-6\omega ^{2}}{(1-\omega ^{2}r^{2})^{2}}}=-6\omega ^{2}+{\mathcal {O}}(\omega ^{4}).}$

Up to the fourth order, this is identical to the constant negative curvature of the hyperbolic space with the line element ${\displaystyle \omega }$

${\displaystyle \mathrm {d} \sigma ^{2}=\mathrm {d} z^{2}+\mathrm {d} r^{2}+{\frac {\sinh ^{2}({\sqrt {3}}\omega r)}{3\omega ^{2}}}\;\mathrm {d} \phi ^{2},}$

${\displaystyle -\infty <z<\infty ,\;\;0<r<\infty ,\;\;-\pi <\phi <\pi }$

and the curvature scalar

${\displaystyle {R}=-6\omega ^{2}.}$

In this sense, the “geometry of the rotating disk” is actually curved and roughly corresponds to the hyperbolic space, as Theodor Kaluza had already suspected in 1910 (without evidence). However, as shown above, there are different ways of measuring distances on the rotating disk, which give very different results. With the Langevin-Landau-Lifschitz metric, as well as with the radar distance in large, the radial distance of a Langevin observer on the ring can be determined with the radius from the rotation center. To do this, the corresponding line element is integrated for the zero geodesics specified above. ${\displaystyle r_{0}}$

${\displaystyle \mathrm {d} r={\frac {\mathrm {d} \phi }{\omega }},\quad \mathrm {d} z=0}$

inserted into the line element results

${\displaystyle \int _{0}^{\Delta }\mathrm {d} \sigma =\int \limits _{0}^{r_{0}}{\left(1+{\frac {\omega ^{2}r^{2}}{1-\omega ^{2}r^{2}}}\right)^{\frac {1}{2}}}\,\mathrm {d} r}$

and further

${\displaystyle \Delta =\int _{0}^{r_{0}}{\frac {\mathrm {d} r}{\sqrt {1-\omega ^{2}\,r^{2}}}}={\frac {\arcsin(\omega r_{0})}{\omega }}=r_{0}+{\frac {\omega ^{2}\,r_{0}^{3}}{6}}+{\mathcal {O}}(r_{0}^{5}).}$

This distance is greater than , while the “radar distance in large” is equal to or less than . ${\displaystyle r_{0}}$ ${\displaystyle r_{0}}$

Since the underlying Langevin-Landau-Lifschitz metric is a Riemann metric, this distance is symmetrical in contrast to the “radial radar distance on a large scale”. The Riemann curvature tensor of the (curved) Langevin-Landau-Lifschitz metric is operationally significant. As Nathan Rosen observed, the local (infinitesimal) distances measured for neighboring Langevin observers agree with those measured by an inertial observer moving parallel and synchronously to them at a given moment.

See also

• History of the special theory of relativity - Rigid bodies and the reality of length contraction
• Paul Ehrenfest
• Non-Euclidean Geometry
• Laser gyro
• Tests of special relativity

swell

Historical treatises

1. ↑ Ehrenfest, P .: Uniform rotation of rigid bodies and the theory of relativity . In: Phys. Magazine . 10, 1909, p. 918.
   • Wikisource (English): Uniform Rotation of Rigid Bodies and the Theory of Relativity
2. ↑ Born, M .: The theory of the rigid electron in the kinematics of the principle of relativity . In: Ann. Phys. . 30, 1909, p. 1. bibcode : 1909AnP ... 335 .... 1B . doi : 10.1002 / andp.19093351102 .
   • Wikisource (English): The Theory of the Rigid Electron in the Kinematics of the Principle of Relativity
3. ↑ Born, M .: On the kinematics of the rigid body in the system of the principle of relativity . In: News from the Society of Science in Göttingen, Mathematical-Physical Class . 2, 1910, pp. 161-179. PPN252457811.
4. ^ Langevin, P .: Remarques au sujet de la Note de Prunier . In: CR Acad. Sci. Paris . 200, 1935, p. 48.

Standard works

1. Grøn, Ø. : Relativistic description of a rotating disk . In: Amer. J. Phys. . 43, No. 10, 1975, pp. 869-876. bibcode : 1975AmJPh..43..869G . doi : 10.1119 / 1.9969 .
2. Landau, LD , Lifschitz, EM : The Classical Theory of Fields (4th ed.) . Butterworth-Heinemann, London 1980, ISBN 0-7506-2768-9 .
   • For the description of the Langevin-Landau-Litschitz metric as the quotient of a Lorentzian manifold by a stationary congruence see Section 84 and the example for the application of a Langevin observer at the end of Section 89 .

Recent references

1. ↑ See the English article Born rigidity
2. ↑ Weber, T., A .: A note on rotating coordinates in relativity . In: American Journal of Physics . 65, No. 6, June 1997, ISSN  0002-9505 , pp. 486-487. doi : 10.1119 / 1.18575 .
   • Thomas A. Weber (* 1934) is a retired professor of theoretical physics at Iowa State University . He received his doctorate from the University of Notre Dame in 1961. He dealt with mathematical physics, relativity theory and formal scattering theory, among other things. In 1997 he was the first to describe in detail the vector field of the basis vectors for Langevin observers. Paul Langevin was the first to use this vector field in 1935 without explicitly describing it, so the Langevin observers characterized by this vector field are named after him.
3. ^ Weber, T., A .: Measurements on a rotating frame in relativity, and the Wilson and Wilson experiment . In: American Journal of Physics . 65, No. 10, October 1997, ISSN  0002-9505 , pp. 946-988. doi : 10.1119 / 1.18696 .
4. ↑ Rizzi, G., Ruggiero, ML: Relativity in Rotating Frames: Relativistic Physics in Rotating Reference Frames . Springer-Science + Business Media Dordrecht, Dordrecht 2004, ISBN 978-90-481-6514-8 , doi : 10.1007 / 978-94-017-0528-8 .
   • Offers a historical overview of Øyvind Grøn's Ehrenfest Paradox , contributions by Neil Ashby , Thomas A. Weber and other authors, a discussion of the Langevin Congruence by Lluís Bel and numerous other references on the subject.
5. ↑ Pauri, M., Vallisneri, M .: Märzke-Wheeler coordinates for accelerated observers in special relativity . In: Found. Phys. Lett. . 13, No. 5, 2000, pp. 401-425. doi : 10.1023 / A: 1007861914639 .
   • Construction of a coordinate system for a Langenvin observer using radar measurements for large distances (see also the Eprint version ).

Remarks

1. ↑ This is an external synchronization . A consequence of this method is that for the clock in the center of rotation, the second of the clocks on the disk is identical to its own second. ${\displaystyle {\rm {O}}}$
2. ↑ The vortex tensor is a skew-symmetrical tensor with three dimensions that can be represented as a three-dimensional vector (vortex vector).
3. ↑ One point means the first derivative according to the affine parameter , two points the second derivative according to the affine parameter . ${\displaystyle \lambda }$ ${\displaystyle \lambda }$

Web links

• The Rigid Rotating Disk in Relativity , by Michael Weiss (1995), from the sci.physics FAQ .
• arxiv : gr-qc / 9904078 : Hrvoje Nikolic: Relativistic contraction and related effects in noninertial frames.
• arxiv : gr-qc / 0207104 : Guido Rizzi, Matteo Luca Ruggiero: Space geometry of rotating platforms: an operational approach.
• arxiv : gr-qc / 0403111 : Olaf Wucknitz: Sagnac effect, twin paradox and space-time topology - Time and length in rotating systems and closed Minkowski space-times.