Cayley graph

The Cayley graph of the free group with two generators a and b

In mathematics , a Cayley graph is a graph that describes the structure of a (usually finitely generated ) group . It depends on a given, usually finite, set of generators of the group .

Arthur Cayley was the first to use graphs to represent groups in 1878; an approach that was further developed by Max Dehn (1911), Otto Schreier (1927) and others. Because of Dehn's great contributions, Cayley graphs were sometimes also called (Dehn's) group pictures . Today Cayley graphs are a central tool in geometric group theory .

definition

Be a group and a generating system . The Cayley graph is a colored and directed graph that is constructed as follows: ${\displaystyle G}$ ${\displaystyle S}$ ${\displaystyle \Gamma =\Gamma (G,S)}$

• A node is assigned to each element of : The node set of is also identified. ${\displaystyle g}$ ${\displaystyle G}$ ${\displaystyle V(\Gamma )}$ ${\displaystyle \Gamma }$ ${\displaystyle G}$
• A color is assigned to each producer from . ${\displaystyle s}$ ${\displaystyle S}$ ${\displaystyle c_{s}}$
• For , the nodes which are to the elements and include, with a directed edge of the color connected. The set of edges therefore consists of pairs of the shape , where the color determines. ${\displaystyle g\in G}$ ${\displaystyle s\in S}$ ${\displaystyle g}$ ${\displaystyle gs}$ ${\displaystyle c_{s}}$ ${\displaystyle E(\Gamma )}$ ${\displaystyle (g,gs)}$ ${\displaystyle s\in S}$

In the geometric group theory it is mostly assumed that the set is finite and symmetrical , that is , and does not contain the neutral element of the group. In this case, apart from the coloring, the Cayley graph is an ordinary graph: its edges are not oriented and it does not contain any loops . ${\displaystyle S}$ ${\displaystyle S=S^{-1}}$

Examples

• Let be the infinite cyclic group and let the set consist of the standard generator 1 and its inverse (−1 in additive notation). The corresponding Cayley graph is then an infinite chain. ${\displaystyle G=\mathbb {Z} }$ ${\displaystyle S}$

• The picture is similar if the finite cyclic group is of order and again consists of two elements, the standard generator 1 of and its inverse; then the Cayley graph is the n-cycle . ${\displaystyle G=\mathbb {Z} /n\mathbb {Z} }$ ${\displaystyle n}$ ${\displaystyle S}$ ${\displaystyle G}$ ${\displaystyle C_{n}}$

• The Cayley graph of the direct product of groups is the Cartesian product of the respective Cayley graphs. The Cayley graph of the free Abelian group with a generator set consisting of the four elements is an infinite lattice in the plane , while the Cayley graph for the direct product with analog generators forms a finite lattice on the torus . ${\displaystyle \mathbb {Z} ^{2}}$ ${\displaystyle (\pm 1,\pm 1)}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {Z} /n\mathbb {Z} \times \mathbb {Z} /m\mathbb {Z} }$ ${\displaystyle n\times m}$

A Cayley graph of the dihedral group D ₄

Another Cayley graph from D ₄

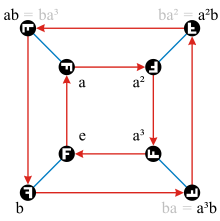
• The Cayley graph of the dihedral group D ₄ with two generators (90 ° rotation clockwise) and (horizontal reflection) is shown on the left. Since it is its own inverse, the blue edges that stand for the execution of are drawn undirected. This choice of and corresponds to the presentation ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle \langle a,b|a^{4}=b^{2}=e,ab=ba^{3}\rangle .\,}$

• The relationships of the group to this choice of generators can be found in the Cayley graph as cycles , for example, a closed path in the graph also provides . ${\displaystyle a^{4}}$ ${\displaystyle aba^{-3}b}$

• The Cayley graph of the free group with two generators and and the quantity is shown above in the article, where the neutral element denotes. Going right on an edge is right multiplication by , while going up is multiplication by . Since the free group has no relations, this graph does not contain any cycles. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle S=\left\{a,b,a^{-1},b^{-1}\right\}}$ ${\displaystyle e}$ ${\displaystyle a}$ ${\displaystyle b}$

characterization

The question of which graphs can appear as Cayley graphs of a group can be answered as follows: The group acts on itself through left multiplication (see also Cayley's theorem ). This effect also provides an effect from on his Cayley graph. Specifically, an element sends a node to the node . The set of edges of the graph is respected by this effect, because an edge is mapped onto the edge . The effect of any group's left multiplication on itself is simply transitive . Accordingly, a Cayley graph is node-transitive . This leads to the following characterization of Cayley graphs: ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle h\in G}$ ${\displaystyle g\in V(\Gamma )}$ ${\displaystyle hg\in V(\Gamma )}$ ${\displaystyle (g,gs)}$ ${\displaystyle (hg,hgs)}$

A graph is a Cayley graph of a group if and only if it allows a simply transitive effect on the node due to the automorphisms of the graph (i.e. mappings that respect the set of edges). ${\displaystyle \Gamma }$ ${\displaystyle G}$ ${\displaystyle G}$

In order to reconstruct the coloring of the graph by the group and the set of producers, one selects a node and labels it with the neutral element of the group. Each node of is then with the unique element of denotes that after mapping. The set of producers of , which yields as Cayley graph, is then the set of labels for the nodes that are adjacent to the selected node . The generation set is finite if and only if the graph is locally finite, i.e. every node is adjacent to a finite number of edges. ${\displaystyle G}$ ${\displaystyle S}$ ${\displaystyle v_{1}\in V(\Gamma )}$ ${\displaystyle v}$ ${\displaystyle \Gamma }$ ${\displaystyle g}$ ${\displaystyle G}$ ${\displaystyle v_{1}}$ ${\displaystyle v}$ ${\displaystyle S}$ ${\displaystyle G}$ ${\displaystyle \Gamma }$ ${\displaystyle v_{1}}$

However, it is not true that every node-transitive graph appears as a Cayley graph, and of course the above statement does not answer all questions about the structure of Cayley graphs. For example, the conjecture that every finite Cayley graph contains a Hamilton cycle, known as the Lovász conjecture , is unproven.

Simple properties

The Cayley graph Γ ( G , S ) depends largely on the choice of producers amount S from. For example, if S has k elements, then every vertex of Γ has k incoming and k outgoing edges. If S is chosen symmetric, then Γ is a regular graph of degree k .

Cycles, that is closed paths, in Cayley provide relations (see presentation of a group ) between the elements of S represent.

If is a surjective group homomorphism that is injective on the generator set S ' of G' , then f induces a superposition of graphs ${\displaystyle f\colon G'\to G}$

${\displaystyle {\bar {f}}\colon \Gamma (G',S')\to \Gamma (G,S),\quad }$where S = f ( S ' ).

In particular, this is the case if a group G of k elements is generated, all of order not equal to 2, and the set S consists of these generators and their inverses. Then the Cayley graph Γ ( G , S ) is overlaid by the infinite regular tree of degree 2 k , which belongs to the free group over the same generators. Such a tree is then a universal overlay of the Cayley graph and is also called a Cayley tree or Bethe grid .

Even if the set S does not create the group G , a graph Γ ( G , S ) can be constructed. However, it will not be connected and will not be considered a Cayley graph. In this case, each connected component corresponds to a coset of the subgroup of S is generated.

Applications in group theory

By studying the Cayley graph one can gain insight into the structure of the group. Among other things, it is interesting to investigate the adjacency matrix , in particular with the means of the spectral theory of graphs , which transfers geometric statements that are obtained from the spectrum of linear operators into a discrete context.

Geometric group theory

For infinite groups which is rough geometry ( coarse geometry ) of the Cayley, or its equivalence class until quasi-isometric , fundamental to the field of geometric group theory . For a finitely generated group it is independent of the choice of a finite set of generators, that is, an intrinsic property of the group. This is only interesting for infinite groups, since all finite groups - for which one can choose - are quasi-isometric to a point. ${\displaystyle S}$ ${\displaystyle S=G}$

The Cayley graph in this context is a metric picture of the group together with the word metric, which is determined by the choice of producers.

Word metrics

The word metric on the Cayley graph is given by the definition that all edges of the graph should have length 1. Equivalently, the distance between two group elements can be defined as the minimum number of factors from the given generating system that can be broken down into, i.e. ${\displaystyle g,h}$ ${\displaystyle gh^{-1}}$

${\displaystyle d(g,h)=\min\{n:gh^{-1}=s_{1}\dots s_{n};s_{1},\dots ,s_{n}\in S\}}$.

The word metric (like the Cayley graph itself) depends on the generating system. For various finite generating systems one obtains quasi-isometric (even bilipschitz-equivalent ) Cayley graphs. All geometric properties of graphs, which are determined except for quasi-isometry, therefore correspond to properties of groups. ${\displaystyle S}$

In geometric group theory one tries to translate algebraic properties of groups into geometric properties of the Cayley graph. A spectacular example of this is Gromow's theorem that a group is virtually nilpotent if and only if its Cayley graph has polynomial volume growth, i.e. H. the volume of the balls from the radius is limited upwards by a polynomial in . ${\displaystyle R}$ ${\displaystyle R}$

Word hyperbolic groups

A group is called word-hyperbolic if its Cayley graph is δ-hyperbolic for one . This means that in every geodetic triangle every point lying on an edge is at a distance from at least one of the other two edges. This definition is (except for the exact value of the constant ) invariant under quasi-isometry and therefore independent of the selected generating system. ${\displaystyle \delta >0}$ ${\displaystyle <\delta }$ ${\displaystyle \delta }$

Examples of word-hyperbolic groups are: finite groups , virtual cyclic groups , finitely generated free groups, fundamental groups of compact surfaces with negative Euler characteristics and, in general, fundamental groups of compact, negatively curved manifolds. In a sense, random groups are word hyperbolic.

Edge at infinity

The Cayley graph has an edge at infinity, formally defined as the set of equivalence classes of geodetic rays, where 2 rays are equivalent if and only if they are finite apart. The effect of the group on the edge at infinity is a “chaotic” dynamic system and encodes many properties of the group.

Examples: for free groups the boundary at infinity is a Cantor set , for fundamental groups of compact negatively curved manifolds the boundary at infinity is a - sphere , but for "most" word-hyperbolic groups the boundary at infinity is a Menger sponge . ${\displaystyle n}$ ${\displaystyle (n-1)}$

history

Cayley initially considered the graphs named after him in 1878 only for finite groups. In his unpublished notes on group theory from 1909-10, Max Dehn introduced the Cayley graph under the name "group picture". Its main application was the solution of the word problem for the fundamental groups of surfaces of gender ≥ 2 with geometric methods, which today belong to the theory of hyperbolic groups . (This is equivalent to solving the topological problem of which curves in the surface can be contracted to one point.) This work was the beginning of today's geometric group theory.

Related constructions

Several objects related to the Cayley graphs can be formed from a presentation of a discrete group.

Cayley complexes

The Cayley complex is a construction very similar to the Cayley graph. It is a cell complex that has the Cayley graph as a 1-skeleton , but in which 2 cells are also glued. For the 2-cells, in addition to the group and the generation set , a choice of relations is required so that a presentation of is. Each relation in provides a cycle for each node in the Cayley graph, along which a 2-cell is glued in. ${\displaystyle G}$ ${\displaystyle S}$ ${\displaystyle R}$ ${\displaystyle (S,R)}$ ${\displaystyle G}$ ${\displaystyle R}$

The Cayley complex of group Z ² with the presentation is, for example, a tiling of the plane with unit squares , the 1-skeleton of which is the Cayley graph of Z ² described above . ${\displaystyle \langle \alpha ,\beta \mid \alpha \beta \alpha ^{-1}\beta ^{-1}=e\rangle }$

Screech graph

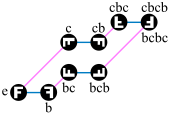
If right secondary classes of a fixed subgroup are selected as nodes instead of elements of the group , a related construction is obtained, the screaming graph , where again a generator set of is. If the trivial subgroup is the Cayley graph again . ${\displaystyle G}$ ${\displaystyle H\subset G}$ ${\displaystyle \Sigma (G,H,S)}$ ${\displaystyle S}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle \Sigma (G,H,S)}$ ${\displaystyle \Gamma (G,S)}$

Individual evidence

1. ↑ Jonathan L. Gross, Thomas W. Tucker: Topological graph theory. Courier Dover Publications, 2001. ISBN 978-0-486-41741-7 . Pp. 10-14. Digitizedhttp: //vorlage_digitalisat.test/1%3Dhttp%3A%2F%2Fbooks.google.ch%2Fbooks%3Fid%3Dmrv9OJVdy_cC~GB%3D~IA%3D~MDZ%3D%0A~SZ%3D~ double-sided%3D~ LT% 3D ~ PUR% 3D
2. ↑ Gromov, M. (2003). Random walk in random groups Geometric and Functional Analysis, 13 (1), 73-146
3. ↑ Cayley, A. (1878). The theory of groups: Graphical representation. Amer. J. Math. 1, 174-176. In his Collected Mathematical Papers 10: 403-405.
4. ↑ Dehn, M. (1987). Papers on Group Theory and Topology. New York: Springer-Verlag. Translated from the German and with introductions and an appendix by John Stillwell, and with an appendix by Otto Schreier.