Clawson point

Similarity center of the height base triangle (red) and the triangle drawn in red, which is formed by the (outer) common tangents of the circles (see dashed lines)

The Clawson point in a triangle is one of the triangle's distinguished points . It can be constructed in the following two ways and has the kimberling number X (19). The point was named after John Wentworth Clawson and examined by Émile Lemoine in 1886 .

definition

For any triangle with angles in the points , the Clawson point is defined as the point with the trilinear coordinates . ${\displaystyle ABC}$ ${\displaystyle \alpha ,\beta ,\gamma }$ ${\displaystyle A,B,C}$ ${\displaystyle \tan(\alpha ):\tan(\beta ):\tan(\gamma )}$

First construction

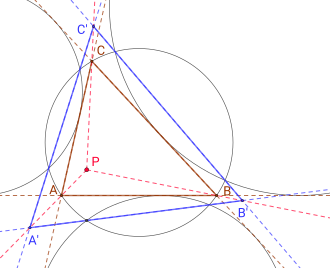
For the given triangle, construct the height base triangle (see adjacent drawing) and the triangle formed by the common outer tangents of two of the three circles . It can be shown that these two triangles have parallel sides in pairs and that the straight lines (dashed in the adjacent drawing) through the corresponding corner points of these two similar triangles intersect at one point, in the so-called similarity center . This point is called the Clawson point. ${\displaystyle ABC}$ ${\displaystyle H_{a}H_{b}H_{c}}$ ${\displaystyle T_{a}T_{b}T_{c}}$

Second construction

Clawson point as the center of perspective of triangle ABC (brown) and the triangle shown in blue, which is bounded by the common chords of a circle and a perimeter (see dashed lines).

Construct the circumference and the circles for the given triangle ABC. Each circle cuts the perimeter in two points, each defining a chord . The extensions of these chords form a triangle (blue in the adjacent drawing), whereby the intersection of the chord extensions is the circle on the sides with the end point , and correspondingly and . One can show that the straight lines , and (dashed red in the adjacent drawing) intersect at a point. In this situation it is also said that the two triangles are in perspective with the point of intersection as the "center of perspective". This point is the Clawson point, that is, it can be shown to coincide with the point of the first construction. ${\displaystyle A'B'C'}$ ${\displaystyle A'}$ ${\displaystyle A}$ ${\displaystyle B'}$ ${\displaystyle C'}$ ${\displaystyle AA'}$ ${\displaystyle BB'}$ ${\displaystyle CC'}$

Barycentric coordinates

The barycentric coordinates of the Clawson point are

${\displaystyle \left({\frac {a}{-a^{2}+b^{2}+c^{2}}}:{\frac {b}{a^{2}-b^{2}+c^{2}}}:{\frac {c}{a^{2}+b^{2}-c^{2}}}\right)}$,

where , and as usual denote the lengths of the sides of the triangle with respect to the corner points , and . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$

literature

• Émile Lemoine : Quelques questions se rapportant à l'étude des antiparallèles des côtés d'un triangle . In: Bulletin de la Société Mathématique de France , Volume 14 (1886), pp. 107–128, especially 114 ( digitized from Nundam)
• JW Clawson, Michael Goldberg: problem 3132. In: The American Mathematical Monthly , Vol. 33, No. 5, 1926, pp. 285-285. ( JSTOR)
• Clark Kimberling : Central Points and Central Lines in the Plane of a Triangle. In: Mathematics Magazine , Vol. 67, No. 3, 1994, pp. 163-187, especially 125. ( JSTOR ).

Web links

• Eric W. Weisstein : Clawson Point . In: MathWorld (English).
• X (19) = CLAWSON POINT and CLAWSON POINT in the Encyclopedia of Triangle Centers (ETC)
• LE POINT CLAWSON PAR LES TRIANGLES ORTHIQUES ET EXTANGENT
• Clawson Point: Orthic Triangle, Extangents Triangle, Homothecy or Homothety

Individual evidence

1. ↑ Antreas P. Hatzipolakis, Paul Yiu: Reflections in Triangle Geometry . In: Forum Geometricorum . tape 9 , 2009, p. 301-348 (English, fau.edu ).
2. ↑ ^{a b} Clark Kimberling: X (19) = CLAWSON POINT in the Encyclopedia of Triangle Centers (accessed 2019-11-30)
3. ↑ ^{a b} Clark Kimberling: CLAWSON POINT . In: Encyclopedia of Triangle Centers (accessed 2019-11-30)
4. ^ JW Clawson, Michael Goldberg: problem 3132. In: The American Mathematical Monthly , Vol. 33, No. 5, 1926, pp. 285-285. ( JSTOR)