Dihydrogen cation

The hydrogen molecular ion , dihydrogen cation , or H ₂ ⁺ , is the simplest molecular ion . It consists of two positively charged protons and one negatively charged electron and can be formed by ionizing the neutral hydrogen molecule .

It is of great historical and theoretical interest because it contains only one electron and therefore no electron-electron interactions occur. Therefore, the electronic Schrödinger equation for this system can be solved analytically in a closed manner with a fixed core distance (so-called Born-Oppenheimer approximation ). The analytical solutions for the energy eigenvalues ​​represent a generalization of the Lambertian W function .

Because of its importance as the simplest molecular system, the hydrogen molecular ion is treated as an example in most textbooks on quantum chemistry . The first successful quantum mechanical treatment of H ₂ ⁺ was published by the Danish physicist Øyvind Burrau in 1927, just one year after Erwin Schrödinger published his fundamental work on wave mechanics . Earlier attempts were published in 1922 by Karel Niessen and Wolfgang Pauli , and in 1925 by Harold Urey . With an overview article from 1928, Linus Pauling made the work of Burrau as well as that of Walter Heitler and Fritz London on the hydrogen molecule known to a larger audience.

The chemical bond in H ₂ ⁺ can be described as a covalent one-electron bond , which has a formal bond order of 1/2.

The hydrogen molecular ion is usually also formed in molecular clouds in space and is of great importance for chemistry in the interstellar medium .

Quantum mechanical treatment, symmetries and asymptotics

Hydrogen molecular ion H2 + with nuclei A and B fixed, nucleus-nucleus distance R and plane of symmetry of the core structure M.

The simplest electronic Schrödinger equation for the hydrogen molecular ion takes into account not only the one electron but also the two nuclei, marked A and B, at fixed positions in space. It can be written as

${\displaystyle \left(-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V\right)\psi =E\psi ~,}$

where is the electron-nucleus Coulomb potential function ${\displaystyle V}$

${\displaystyle V=-{\frac {e^{2}}{4\pi \varepsilon _{0}}}\left({\frac {1}{r_{a}}}+{\frac {1}{r_{b}}}\right)}$

is, and is the (electronic) energy of a given quantum mechanical state (eigenstate), with the electronic state function that depends on the position coordinates of the electron. An additive term , which is a constant for a given core-core distance , has been left out in the potential function , since it only shifts the eigenvalue. The distances between the electron and the nuclei are denoted by and . In atomic units , the Schrödinger equation becomes ${\displaystyle E}$ ${\displaystyle \psi =\psi (\mathbf {r} )}$ ${\displaystyle 1/R}$ ${\displaystyle R}$ ${\displaystyle V}$ ${\displaystyle r_{a}^{}}$ ${\displaystyle r_{b}^{}}$ ${\displaystyle (\hbar =m=e=4\pi \varepsilon _{0}=1)}$

${\displaystyle \left({}-{\frac {1}{2}}\nabla ^{2}+V\right)\psi =E\psi \qquad {\mbox{mit}}\qquad V={}-{\frac {1}{r_{a}^{}}}-{\frac {1}{r_{b}^{}}}\;.}$

The midpoint between the positions of the cores can be chosen as the origin of the coordinates. From general symmetry principles it follows that the state functions can be characterized according to their symmetry behavior with respect to space inversion . There are state functions ${\displaystyle (\mathbf {r} \to -\mathbf {r} )}$

${\displaystyle \psi _{+}(\mathbf {r} )}$,

which are "symmetrical" with respect to space inversion, and state functions

${\displaystyle \psi _{-}(\mathbf {r} )}$,

which are anti-symmetric under this symmetry operation : ${\displaystyle \psi _{\pm }(-{\mathbf {r} })={}\pm \psi _{\pm }({\mathbf {r} })\;.}$

We note that the permutation (exchange) of the nuclei has the same effect on the electronic state functions. For a multi-electron system, in addition to the symmetries just mentioned, the correct symmetry behavior of the state function with regard to permutations of the electrons ( Paul’s exclusion principle ) must be guaranteed. The Schrödinger equations for the symmetry-adjusted state functions are now ${\displaystyle \psi }$

${\displaystyle {\begin{aligned}\left(-{\frac {1}{2}}\nabla ^{2}+V\right)\psi _{+}=E_{+}\psi _{+}\\\left(-{\frac {1}{2}}\nabla ^{2}+V\right)\psi _{-}=E_{-}\psi _{-}\end{aligned}}}$

The ground state (the energetically lowest discrete state) of the is the state, the associated state function is usually marked with . The state function of the first excited state,, is marked with . The suffixes g and u (of even and odd ) appearing here characterize the symmetry behavior under space inversion. Their use is standard for the identification of electronic states of diatomic molecules, while the designations e and o (from English "even" and "odd" ) are used for the states of atoms . ${\displaystyle {\text{H}}_{2}^{+}}$ ${\displaystyle {\rm {X}}_{}^{2}\Sigma _{\rm {g}}^{+}}$ ${\displaystyle \psi _{+}}$ ${\displaystyle 1s\sigma _{\rm {g}}^{}}$ ${\displaystyle \psi _{-}}$ ${\displaystyle {\rm {A}}_{}^{2}\Sigma _{\rm {u}}^{+}}$ ${\displaystyle {\rm {2p}}\sigma _{\rm {u}}^{}}$

Energies (E) of the lowest discrete states of the hydrogen molecular ion as a function of the core-core distance (R) in atomic units. See text for more details. ${\displaystyle {\text{H}}_{2}^{+}}$

For large core-core distances, the (total) energy eigenvalues for these two lowest states have the same asymptotic expansion in reciprocal powers of the core-core distance R : ${\displaystyle E_{\pm }}$

${\displaystyle E_{\pm }={}-{\frac {1}{2}}-{\frac {9}{4R^{4}}}+O(R^{-6})+\cdots }$

The actual difference between these two energies is called the exchange energy splitting and is given by:

${\displaystyle \Delta E=E_{-}-E_{+}={\frac {4}{e}}\,R\,e^{-R}\left[\,1+{\frac {1}{2R}}+O(R^{-2})\,\right]}$

This expression disappears exponentially as the core-core distance increases. The leading term was only correctly obtained with the Holstein-Herring method . In a very similar way, asymptotic expansions in powers of up to high order were found by Čížek et al. obtained for the lowest ten discrete states of the hydrogen molecular ion (for the case of pinned nuclei). For any diatomic or polyatomic molecular systems, it is very difficult to calculate the exchange energy splitting with a large core-core distance. However, knowledge of them is necessary for the treatment of long-range interactions, including studies relating to magnetism and charge exchange effects. The effects mentioned are particularly important for the physical understanding of stars and atmospheres (terrestrial and extraterrestrial). ${\displaystyle {\textstyle {\frac {4}{e}}}Re^{-R}}$ ${\displaystyle 1/R}$

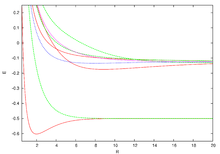
The energies for the lowest discrete states are shown in the figure above. The values ​​can be obtained with any desired accuracy using a computer algebra program from the "generalized" Lambertian W-function (see Eq. There and the reference to the work of Scott, Aubert-Frécon, and Grotendorst) but they were initially obtained numerically, in double precision, using the most precise computer program available called ODKIL. The red solid lines are states. The green dashed lines are states. The blue dashed line is a state and the pink dotted line is a state. Although the eigenvalue solutions obtained with the help of the “generalized” Lambertian W function replace these asymptotic developments, they are very useful in practice, especially in the vicinity of the equilibrium distance. Such solutions are possible because the partial differential equation that represents the Schrödinger equation can be separated into two coupled ordinary differential equations using prolate spheroidal coordinates . ${\displaystyle (3)}$ ${\displaystyle {\rm {}}_{}^{2}\Sigma _{\rm {g}}^{+}}$ ${\displaystyle {\rm {}}_{}^{2}\Sigma _{\rm {u}}^{+}}$ ${\displaystyle {\rm {}}_{}^{2}\Pi _{\rm {u}}}$ ${\displaystyle {\rm {}}_{}^{2}\Pi _{\rm {g}}}$

education

The hydrogen molecular ion is formed in nature by the effect of cosmic rays on hydrogen molecules. An electron is knocked out and leaves the cation behind.

${\displaystyle \mathrm {H_{2}+Kosmische\ Strahlung\longrightarrow H_{2}^{+}+e^{-}+Kosmische\ Strahlung} }$

The particles of cosmic rays have enough energy to ionize many molecules before they are stopped themselves.

The maximum cross-section for very fast protons (70 keV) is 2.5 × 10 ⁻¹⁶  cm ² .

In nature, the ion continues to react with other hydrogen molecules:

${\displaystyle \mathrm {H_{2}^{+}+H_{2}\longrightarrow H_{3}^{+}+H} }$

properties

The ionization energy of the hydrogen molecule is the dissociation energy . ${\displaystyle 15{,}603\,\mathrm {eV} }$ ${\displaystyle 1{,}8\,\mathrm {eV} }$

Individual evidence

1. ^ TC Scott, M. Aubert-Frécon, J. Grotendorst: New Approach for the Electronic Energies of the Hydrogen Molecular Ion. In: Chem. Phys. 324, 2006, pp. 323-338, doi: 10.1016 / j.chemphys.2005.10.031 , arxiv : physics / 0607081 .
2. ↑ Ø. Burrau: Calculation of the energy value of the hydrogen molecule ion (H2 +) in the normal state . In: Danske Vidensk. Selskab. Math.-fys. Meddel. . M 7:14, 1927, pp. 1-18.
3. ↑ Øjvind Burrau: The calculation of the energy value of hydrogen molecule ions (H ₂ ⁺ ) in their normal position . In: Natural Sciences . 15, No. 1, 1927, pp. 16-17. doi : 10.1007 / BF01504875 .
4. ↑ Karel F. Niessen On the quantum theory of the hydrogen molecule ion , dissertation, Utrecht University, Utrecht: I. van Druten (1922), cited in J. Mehra, Volume 5, Part 2, 2001, p. 932.
5. ↑ W. Pauli: About the model of the hydrogen molecule ion . In: Ann. d. Phys. . 373, No. 11, 1922, pp. 177-240. doi : 10.1002 / andp.19223731101 . advanced dissertation; Received March 4, 1922, published in issue No. 11 of August 3, 1922.
6. ^ Urey HC: The Structure of the Hydrogen Molecule Ion . In: Proc. Natl. Acad. Sci. USA . 11, No. 10, October 1925, pp. 618-21. doi : 10.1073 / pnas.11.10.618 . PMID 16587051 . PMC 1086173 (free full text).
7. ^ L. Pauling: The Application of the Quantum Mechanics to the Structure of the Hydrogen Molecule and Hydrogen Molecule-Ion and to Related Problems . In: Chemical Reviews . 5, 1928, pp. 173-213. doi : 10.1021 / cr60018a003 .
8. ^ Clark R. Landis, Frank Weinhold: Valency and bonding: a natural bond orbital donor-acceptor perspective . Cambridge University Press, Cambridge, UK 2005, ISBN 0-521-83128-8 , pp. 96-100.
9. ↑ K.-P. Huber, Gerhard Herzberg : Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules. Van Nostrand Reinhold, New York 1979.
10. ↑ Jiří Cížek, Robert J. Damburg, Sandro Graffi, Vincenzo Grecchi, Evans M. Harrell, Jonathan G. Harris, Sachiko Nakai, Josef Paldus, Rafail Kh. Propin, Harris J. Silverstone: 1 / R expansion for H2 +: Calculation of exponentially small terms and asymptotics . In: Physical Review A . tape 33 , no. 1 , 1986, pp. 12–54 , doi : 10.1103 / PhysRevA.33.12 .
11. ^ TC Scott, Alexander Dalgarno , JD Morgan III: Exchange Energy of H2 + Calculated from Polarization Perturbation Theory and the Holstein-Herring Method. In: Phys. Rev. Lett. 67, 1991, pp. 1419-1422. doi: 10.1103 / PhysRevLett.67.1419
12. ↑ G. Hadinger, M. Aubert Frécon, G. Hadinger: The Killing Beck method for the one-electron two-center a problem. In: Journal of Physics B. 22, 1989, pp. 697-712, doi: 10.1088 / 0953-4075 / 22/5/003 .
13. ↑ E. Herbst: The Astrochemistry of H ₃ ⁺ . In: Phil. Trans. R. Soc. Lond. A. 2000, 358, 1774, pp. 2523-2534, doi: 10.1098 / rsta.2000.0665 .