Unit distance graph

from Wikipedia, the free encyclopedia
The Petersen graph is a unit distance graph: it can be drawn so that each edge is the same length.

A unit distance graph is a geometric graph in which each edge is the same length. Edges of a unit distance graph may intersect, i.e. H. the graph does not always have to be planar . A unit distance graph without intersections is called a matchstick graph .

The problem of Hadwiger and Nelson deals with the chromatic number of the graph. Each unit distance graph can be colored with a maximum of seven colors , but it is well known that there are also some graphs that require at least four colors. Another known open problem deals with the question of how high the ratio of the number of edges to the number of nodes can be.

Examples

Hypercube graph Q 4 as a unit distance graph.

The following graphs are unit distance graphs:

Strict unit distance graph

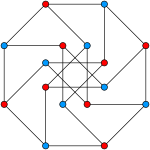
Unit distance variant of the Möbius – Kantor graph , in which some non-adjacent nodes also have a unit distance.

Some definitions in the literature allow the possibility that non-adjacent pairs of nodes may also have a unit distance. For example, there is a variant of the Möbius – Kantor graph of this type.

According to this weakened definition, all generalized Petersen graphs are unit distance graphs. To distinguish between the two definitions, a graph in which only neighboring nodes are allowed to have a unit distance is called a strict unit distance graph .

If you remove a spoke from the wagon wheel W 7 , you get a non-strict subgraph . It is not possible to arrange the nodes and in particular the two end points of the missing spoke in such a way that one again obtains a strict graph.

Counting unit distances

In 1946 Paul Erdős posed the problem of how to determine the number of pairs of points with a unit distance in a set of n points. In terms of graph theory , how dense can a unit distance graph be?

The hypercube graph has a lower bound for the number of unit distances proportional to n · log n . If the points are arranged in a square grid with carefully chosen spaces, there is an improved lower bound of according to Erdős

Erdős offered a cash prize of $ 500 in case someone finds a similar function for the upper bound. The best known upper bound so far is proportional to

This limit can also be viewed as a count of the incidences between points and unit circles, and is closely related to Szemerédi and Trotter's theorem for incidences between points and lines . The problem (Erdös' unit distance problem) is still open. Erdös assumed that the number of points with a unit distance was in the order of magnitude of the lower bound.

Generalization for higher dimensions

The definition of the unit distance graph can of course also be generalized to higher-dimensional Euclidean spaces . Each graph can be embedded as a point set in a sufficiently high dimension. Maehara and Vojtěch Rödl showed in 1990 that the necessary dimension to embed a graph in this way is limited by twice the maximum degree of the graph.

The necessary dimension to embed a graph in such a way that all edges have a unit distance, and the dimension necessary to embed a graph in such a way that all edges correspond exactly to the unit distance pairs, can differ greatly from each other: the Johnson graph with 2n nodes can be embedded in the fourth dimension in such a way that all of its edges have unit distance, but requires n - 2 dimensions for an embedding in which only the edges are unit distance pairs.

See also

literature

  • FS Beckman, DA Quarles: On isometries of Euclidean spaces . In: Proceedings of the American Mathematical Society . tape 4 , 1953, pp. 810-815 ( MR0058193 ).
  • Paul Erdős : On sets of distances of n points . In: American Mathematical Monthly . tape 53 (5) . The American Mathematical Monthly, vol. 53, no. 5, 1946, pp. 248-250 , doi : 10.2307 / 2305092 , JSTOR : 2305092 .
  • Paul Erdős , Miklós Simonovits: On the chromatic number of geometric graphs . In: Ars Combinatoria . tape 9 , 1980, pp. 229-246 .
  • Eberhard H.-A. Gerbracht: Eleven unit distance embeddings of the Heawood graph . 2009, arxiv : 0912.5395 .
  • Severino V. Gervacio, Yvette F. Lim, Hiroshi Maehara: Planar unit-distance graphs having planar unit-distance complement . In: Discrete Mathematics . tape 308 (10) , 2008, pp. 1973-1984 , doi : 10.1016 / j.disc.2007.04.050 .
  • Greg Kuperberg : The Erdos kitty: At least $ 9050 in prizes! 1992 (posting in the Usenet group rec.puzzles and sci.math).
  • Hiroshi Maehara: Distances in a rigid unit-distance graph in the plane . In: Discrete Applied Mathematics . tape 31 (2) , 1991, pp. 193-200 , doi : 10.1016 / 0166-218X (91) 90070-D .
  • Hiroshi Maehara: Extending a flexible unit-bar framework to a rigid one . In: Discrete Mathematics . tape 108 (1-3) , 1992, pp. 167-174 , doi : 10.1016 / 0012-365X (92) 90671-2 ( MR1189840 ).
  • Hiroshi Maehara, Vojtech Rödl: On the dimension to represent a graph by a unit distance graph . In: Graphs and Combinatorics . tape 6 (4) , 1990, pp. 365-367 , doi : 10.1007 / BF01787703 .
  • Alexander Soifer : The Mathematical Coloring Book . Springer-Verlag, 2008, ISBN 978-0-387-74640-1 .
  • Joel Spencer , Endre Szemerédi , William T. Trotter: Unit distances in the Euclidean plane . In: Graph Theory and Combinatorics . Academic Press, 1984, pp. 293-308 .
  • Apoloniusz Tyszka: Discrete versions of the Beckman-Quarles theorem . In: Aequationes Mathematicae . tape 59 (1-2) , 2000, pp. 124-133 , doi : 10.1007 / PL00000119 ( MR1741475 ).
  • Arjana Žitnik, Boris Horvat, Tomaž Pisanski : All generalized Petersen graphs are unit-distance graphs . tape 1109 , 2010 ( online [PDF; 377 kB ] IMFM preprints).

Web links

Individual evidence

  1. ↑ Žitnik, Horvat and Pisanski, 2010.
  2. ↑ Gervacio, Lim and Maehara, 2008.
  3. ↑ Soifer, 2008, p. 94.
  4. ↑ Kuperberg, 1992.
  5. ↑ Joel Spencer, Endre Szemerédi and William Trotter, 1984.
  6. ↑ Endre Szemeredi, Erdös unit distance problem, in: John Forbes Nash jr., Michael Th. Rassias (eds.), Open problems in mathematics, Springer 2016, pp. 459–478
  7. ↑ Erdős and Simonovits, 1980.