Case with air resistance
The fall with air resistance is the falling movement of a body, for example that of a parachutist , in which the air resistance does not allow the movement to run as free fall .
Difference to free fall
Without air resistance, if the body falls close to the earth, the speed of the falling body increases by 9.81 m / s per second. Fall is thus a uniformly accelerated movement . This means that the speed increases linearly with the elapsing fall time. The acceleration is the acceleration due to gravity. After one second the falling body has a speed of 35 km / h in relation to the earth's surface, after two seconds 71 km / h and after three seconds 106 km / h. A skydiver would have reached a speed of over 2100 km / h after a minute in free fall.
In fact, a skydiver is also affected by air resistance, which increases quadratically with speed. The resulting acceleration therefore only corresponds to the acceleration due to gravity at the beginning, afterwards it decreases until after about seven seconds the acceleration becomes zero - the parachutist now falls at the limit speed of the human body of approx. 55 m / s (approx. 198 km / h ). However, this speed is not the maximum achievable speed, but the one that is reached when taking the stable, perpendicular to the fall position with arms and legs spread. In a straight, upright posture head first, the air resistance is significantly lower. Speeds of just over 500 km / h are reached.
Calculation with differential equations
Free fall considers the fall of a body in a gravitational field without the influence of a surrounding medium or atmosphere. This is often a reasonable approximation at low speeds. However, if the acceleration is to be determined exactly, the lift, the Stokes friction and the Newton friction must be taken into account.
Fall with buoyancy
The surrounding medium acts on the body with a force which corresponds to the weight of the mass of the displaced medium and which is directed in the opposite direction. The lift is negligible when the ratio holds, where is the density.
For example, the buoyancy of balloons in the air or people in the water cannot be neglected.
The buoyancy is:
where is the volume of the body, its density and the density of the displaced medium. We define
as lift acceleration. So we get for the whole force:
in which
is referred to as the adjusted acceleration of gravity. The solution for this differential equation is then analogous to free fall:
Note that it can also be negative, if .
Case with Stokes friction
At low speeds, the friction is proportional to the speed of fall:
with a coefficient of friction . The equation of motion in the z-direction (vertical) is therefore
or.
This equation leads to the expressions
for the speed and
for the height. Both the speed and the distance covered by the falling object depend on its mass, which corresponds to everyday experience. The limit speed that would be set for a free fall with Stokes friction is
Case with air resistance: Newton friction
From a certain critical speed (see Reynolds number ), the laminar air flow past the body turns into a turbulent one. As a result, the air resistance now depends on the square of the speed:
From the equation of motion for a downward movement (i.e. v <0), the differential equation follows
- .
This differential equation is of the Riccat type and can therefore be solved analytically if a particular solution is known. A particulate solution corresponds to the steady state
- .
This results in the speed
where tanh (x) of the hyperbolic tangent , artanh (x) of the Area hyperbolic tangent and is and must apply.
The path then results directly as the integral of the speed over time
where the natural logarithm , the hyperbolic cosine and is.
Since the speed is included in the equation of motion as a square, the change in sign in the case of a reversal of motion in the friction term must be explicitly taken into account by differentiation between cases. The general equation of motion is therefore
- .
The solutions for times with (momentary movement upwards) follow from the above solutions through the substitution . The constant depends on the shape of the body and the density of the flowing medium (e.g. air). The following applies:
- ,
where is the drag coefficient , the body cross-sectional area and the density of the surrounding medium (air).
Example: meteoroid
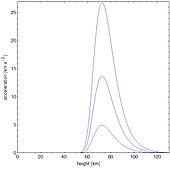
In the following it is assumed that a spherical meteoroid with the cross-section and the mass penetrates the earth's atmosphere and is slowed down in the process. Find the speed and braking acceleration of the meteoroid as a function of the height above the ground. Pure Newton friction is assumed, i.e. H. Effects from supersonic, heating of the air and pressure reduction close to vacuum are neglected. The gravitational acceleration of the earth decreases with increasing height above the earth's surface. It applies
- ,
where denotes the radius of the earth. According to the barometric altitude formula , the air density is at this altitude
Here is the air density on the ground, the mean molar mass of the atmospheric gases (0.02896 kg mol −1 ), the universal gas constant (8.314 JK −1 mol −1 ) and the absolute temperature . The flow resistance of the air at speed depends on this density:
The effective acceleration on the meteoroid of mass m corresponds to the gravitational acceleration minus the braking acceleration:
If we put the above formulas into this equation, we get the equation of motion of the meteoroid:
In the adjacent diagrams, the equation of motion for an iron meteorite with the volume V = 1 cm³ and the mass m = 7.874 g was solved numerically . The meteoroid has the initial speeds v 0 1 = 15 km / s, v 0 2 = 25 km / s or v 0 3 = 35 km / s. It turns out that such a body is always braked in the same height range, with a larger mass merely shifting all curves in the diagrams to the left with the same density. Since an acceleration of 1 km / s² corresponds to about 102 times the acceleration of gravity, fast meteoroids are exposed to an enormous force, which tears them into fragments and burns them up due to the high frictional heat. The resulting light makes up a small part of the luminous appearance of a falling star .
See also
Web links
- Free fall with and without air resistance (PDF; 484 kB) with derivation of air resistance.






















































