Gravimetry

The term gravimetry (from Latin gravitas , "gravity" and -metry from Greek τὸ μέτρον - the measure) describes the methods with which the local and regional gravity field of the earth is measured. The determination of this fundamental potential field is equally important for geodesy, geophysics and technology.

In Geodesy are local gravity values for the height determination (exact reduction of leveling ) and the geoid determination of significance in geophysics and geodynamics for the exploration of the Earth's interior and its movements. Furthermore, precise scales and other technical measuring methods require gravimetric data for their calibration .

Based on the different strengths of the gravitational acceleration at different locations, statements can be made about the distribution of the masses in the earth's crust and the respective rock density . However, the interpretation is not always clear ( inversion problem of potential theory ). Gravity measurement is also gaining in importance when researching other celestial bodies ( planetology , earth's moon ).

Earth's gravitational field in the Southern Ocean. Blue = negative deviation, red tones = positive deviation.

Measurement principles

Gravitation can be determined, for example, from the period of oscillation of a pendulum or with a rotary balance , but the accuracy is limited to a few millionths of gravity. With modern gravimeters , which work according to the spring balance principle, relative measurement uncertainties down to 5 · 10 ⁻⁹ can be achieved, with superconducting gravimeters even down to 10 ⁻¹¹ . In the last 15 years, methods of matter wave interferometry of cold atoms have been used to demonstrate absolute gravimeters with measurement uncertainties of the order of 10 ⁻¹⁰ . With the " free fall " measuring principle (in a vacuum), the gravity can also be determined absolutely . A test mass of 10 ⁶ to 10 ⁷ rubidium atoms is dropped in a magnetically shielded high vacuum chamber at a temperature of approximately 1 µK and the downward movement is measured with an ultra-high resolution. Another way to measure relative differences in gravity is to use clock rate differences. According to the theory of relativity , the speed of clocks depends on their position in the gravitational field. Current atomic clocks achieve accuracies in the range of 10 ⁻¹⁸ , which means that heights in the gravitational field in the centimeter range can be determined relative to one another.

For later retrieval of the gravimeter points and for the precise reduction of the measurements, the geographical or national coordinates of the measuring points must be determined. This is done i. d. Usually by local measurement . The local environment including the blocked dimensions is documented in point descriptions .

Terrain reduction and interpretation

Before an exact interpretation of the measurement results (exploration of the earth's crust or the earth's gravity field ), they must be reduced by the influence of the terrain . This calculation step is called "terrain reduction " or " topographical reduction ". In the past it was determined with foils on maps , today it is calculated with digital terrain models ( DTM ). The typical distance between the points of a DTM is between 50 m and 500 m.

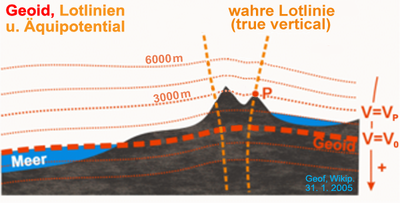
Mountains bend the plumb line by up to 0.01 ° and change the force of gravity by up to 0.02%, which is why a reduction in the terrain is necessary. Gravity is related to the mutual distance of the level surfaces, while the plumb lines on them (and on the geoid) are always perpendicular.

These reductions and the remaining gravity anomalies can reach over 200 milligals , which is 0.02% of the average gravitational acceleration . The anomalies provide information about geological irregularities in the subsurface, which are caused by different densities of different rocks , by oil or ore deposits or by different depths of the earth's mantle. They are often used in exploration to locate deposits .

Another application of gravimetry is the determination of level surfaces of the earth's gravitational field for geoid determination . The geoid deviates globally by ± 50 meters (maximum 110 m) from the earth's ellipsoid and can be determined by well distributed gravity measurements with accuracies of a few centimeters to decimeters.

Gravimetric methods

They are called “gravimetric”

Methods that determine the course of the geoid or the level surfaces by measuring gravity , or
Methods of applied geophysics , which researches raw materials and rocks in the earth's crust by calculating gravity anomalies - in contrast to seismic, electrical or magnetic methods.

In flat countries, these methods are particularly economical . In the mountains, on the other hand, the effects of the terrain on gravity are difficult to determine. Therefore other methods are more advantageous there, e.g. B. the astrogeodetic geoid determination (measurement of the vertical deviation ) or seismic methods .

literature

Wolfgang Torge : Gravimetry. de Gruyter-Verlag, Berlin 1989, ISBN 978-3-11-010702-9 , textbook, 477 pp.
Karl Ledersteger : Astronomical and Physical Geodesy (Earth Measurement) , JEK Volume VJBMetzler-Verlag, Stuttgart 1968
WA Magnitsky : Theory of the Figure of the Earth. Textbook of Gravimetry, Moscow 1961 (Russian) and Verlag für Bauwesen (East Berlin) 1964, 340 pp.
Alexander A. Kaufman, Richard O. Hansen: Principles of the gravitational method. Elsevier, Amsterdam 2008, ISBN 978-0-444-52993-0
Jakob Flury: Future satellite gravimetry and earth dynamics. Springer, Dordrecht 2005, ISBN 0-387-29796-0
Rune Floberghagen: Lunar gravimetry. Kluwer, Dordrecht 2002, ISBN 1-4020-0544-X

Individual evidence

↑ Steven Chu, Achim Peters, Keng Yeow Chung: Measurement of gravitational acceleration by dropping atoms. In: Nature. 1999, 400, pp. 849-852, doi: 10.1038 / 23655 .
↑ Ménoret, V .; Vermeulen, P .; Desruelle, B .; et al: Gravity measurements below 10-9 g with a transportable absolut quantum gravimeter. Nature, ScientificReports 8, 2018, accessed on August 17, 2018 .
↑ TL Nicholson, SL Campbell, RB Hutson, GE Marti, BJ Bloom, RL McNally, W. Zhang, MD Barrett, MS Safronova, GF Strouse, WL Tewn J. Ye: Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. In: Nature Communications. 2015, 6, doi: 10.1038 / ncomms7896

[1] Steven Chu, Achim Peters, Keng Yeow Chung: Measurement of gravitational acceleration by dropping atoms. In: Nature. 1999, 400, pp. 849-852, doi: 10.1038 / 23655 .

[2] Ménoret, V .; Vermeulen, P .; Desruelle, B .; et al: Gravity measurements below 10-9 g with a transportable absolut quantum gravimeter. Nature, ScientificReports 8, 2018, accessed on August 17, 2018 .

[3] TL Nicholson, SL Campbell, RB Hutson, GE Marti, BJ Bloom, RL McNally, W. Zhang, MD Barrett, MS Safronova, GF Strouse, WL Tewn J. Ye: Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. In: Nature Communications. 2015, 6, doi: 10.1038 / ncomms7896