Hyperbolic movement

The hyperbolic movement of accelerated objects along the axis can be visualized using a Minkowski diagram . Each hyperbola is defined by and (with ) in equation   (2) ${\displaystyle X}$ ${\displaystyle x=\pm c^{2}/\alpha }$ ${\displaystyle \eta =\alpha \tau /c}$ ${\displaystyle c=1,\alpha =1}$

The hyperbolic is in the special theory of relativity , the movement of an object with a constant self-acceleration , this acceleration of a moving observer by means of the acceleration sensor is measured. The name hyperbola movement comes from the fact that the equation for the path of this object in the Minkowski diagram corresponds to a hyperbola . This movement has some interesting properties, such as the ability to leave the light behind if there is a sufficient lead. For a general overview of accelerations in Minkowski spacetime see Acceleration (Special Theory of Relativity) .

In addition, it is possible to represent this movement in an accelerated reference system by using hyperbolic coordinates. These coordinates can be further subdivided with regard to the position of the accelerated observer or the length measurement used. The expressions Rindler coordinates, Møller coordinates, Kottler-Møller coordinates, radar coordinates, Lass coordinates are known, all of these systems being often referred to as Rindler coordinates.

The hyperbolic movement and the hyperbolically accelerated frame of reference were already discussed in the early days of the SRT, often in connection with Born's rigidity . Corresponding relationships for flat space-time can be found in Albert Einstein (1907, 1912), Max Born (1909), Gustav Herglotz (1909), Arnold Sommerfeld (1910), Max von Laue (1911), Hendrik Lorentz (1913), Friedrich Kottler (1914), Wolfgang Pauli (1921), Karl Bollert (1922), Stjepan Mohorovičić (1922), Georges Lemaître (1924), Einstein & Nathan Rosen (1935), Christian Møller (1943, 1952), Fritz Rohrlich (1963), Harry Lass (1963), and for the flat as well as curved spacetime in general relativity in Wolfgang Rindler (1960, 1966). See the history section for details .

World line

The self- acceleration of a particle is defined as the acceleration it experiences when it changes from one inertial system to another. If is parallel to the direction of movement, then there is the following relation to the usual three-fold acceleration : ${\displaystyle \alpha }$ ${\displaystyle \alpha }$ ${\displaystyle a=du/dT}$

${\displaystyle \alpha =\gamma ^{3}a={\frac {1}{\left(1-u^{2}/c^{2}\right)^{3/2}}}{\frac {du}{dT}},}$

where is the instantaneous speed of the particle, the Lorentz factor , the speed of light and the coordinate time, measured in the external inertial system . The equations of the world line resulting from this through integration can be expressed as a function of the coordinate time as well as the proper time of the particle. If all initial values ​​for time, location and speed are set to 0, they have the following form: ${\displaystyle u}$ ${\displaystyle \gamma }$ ${\displaystyle c}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle \tau }$

${\displaystyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {\alpha T}{\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}}\\&=c\tanh \left(\operatorname {asinh} {\frac {\alpha T}{c}}\right)\\X(T)&={\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}-1\right)\\&={\frac {c^{2}}{\alpha }}\left(\cosh \left(\operatorname {asinh} {\frac {\alpha T}{c}}\right)-1\right)\\c\tau (T)&={\frac {c^{2}}{\alpha }}\ln \left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}+{\frac {\alpha T}{c}}\right)\\&={\frac {c^{2}}{\alpha }}\operatorname {asinh} {\frac {\alpha T}{c}}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh {\frac {\alpha \tau }{c}}\\\\X(\tau )&={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)\\\\cT(\tau )&={\frac {c^{2}}{\alpha }}\sinh {\frac {\alpha \tau }{c}}\\\\\\\end{aligned}}\end{array}}}$		(1)

The particle is at the time and describes the hyperbola . However, if the initial values ​​are not 0, it follows: ${\displaystyle X=0}$ ${\displaystyle T=0}$ ${\displaystyle \left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}}$

${\displaystyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {u_{0}\gamma _{0}+\alpha T}{\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}}\quad \\&=c\tanh \left\{\operatorname {asinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right\}\\X(T)&=X_{0}+{\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}-\gamma _{0}\right)\\&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {asinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right]-\gamma _{0}\right\}\\c\tau (T)&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\ln \left({\frac {{\sqrt {c^{2}+\left(u_{0}\gamma _{0}+\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T}{\left(c+u_{0}\right)\gamma _{0}}}\right)\\&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\left\{\operatorname {asinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)-\operatorname {atanh} \left({\frac {u_{0}}{c}}\right)\right\}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh \left\{\operatorname {atanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right\}\\\\X(\tau )&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {atanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-\gamma _{0}\right\}\\\\cT(\tau )&=cT_{0}+{\frac {c^{2}}{\alpha }}\left\{\sinh \left[\operatorname {atanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-{\frac {u_{0}\gamma _{0}}{c}}\right\}\end{aligned}}\end{array}}}$

Rapidity

To simplify the position

${\displaystyle X={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)}$

to be subjected to a spatial shift , so ${\displaystyle c^{2}/\alpha }$

${\displaystyle X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}}$,

whereby the particle is in position at the time . If now and by introducing rapidity , the equations of hyperbolic motion are reduced to ${\displaystyle X=c^{2}/\alpha }$ ${\displaystyle T=0}$ ${\displaystyle x=c^{2}/\alpha }$ ${\displaystyle \eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}}$

${\displaystyle cT=x\sinh \eta ,\quad X=x\cosh \eta }$		(2)

with the hyperbola . ${\displaystyle X^{2}-c^{2}T^{2}=x^{2}}$

Charged particles

Born (1909), Sommerfeld (1910), von Laue (1911) and Pauli (1921) also formulated the equations for the electromagnetic field of charged particles in hyperbolic motion. This was continued by Hermann Bondi & Thomas Gold (1955) and Fulton & Fritz Rohrlich (1960)

${\displaystyle {\begin{aligned}E_{\rho '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 'z'}{\xi ^{\prime 3}}}\\E_{z'}'=&{\frac {-\left(4e/\alpha ^{2}\right)1/\alpha ^{2}+t^{\prime 2}+\rho ^{\prime 2}-z^{\prime 2}}{\xi ^{\prime 3}}}\\E_{\varphi '}'=&H_{\varphi '}'=H_{z'}'=0\\H_{\varphi '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 't'}{\xi ^{\prime 3}}}\\\xi '=&{\sqrt {\left(1/\alpha ^{2}+t^{\prime 2}-\rho ^{\prime 2}-z^{\prime 2}\right)^{2}+\left(2\rho '/\alpha \right)^{2}}}\end{aligned}}}$

This is related to the controversial question of whether or not charges radiate in perpetual hyperbolic movement, and whether this is compatible with the equivalence principle - although it is only a hypothetical question, since perpetual hyperbolic movement is not possible. Early authors such as Born (1909) or Pauli (1921) assumed that no radiation occurs, but it was later shown by Bondi & Gold and Fulton & Rohrlich that radiation does occur.

Rindler coordinates

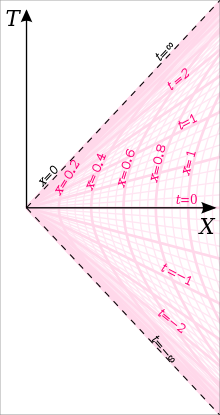
Rindler coordinates for in equation   (2) , on a Minkowski diagram. The dashed lines correspond to the Rindler horizon. ${\displaystyle \alpha =0{,}5}$

In equation   (2) for the hyperbolic movement, the expression was used as a constant, whereas the rapidity is a variable. As, for example, Sommerfeld (1910) pointed out, the reverse can also be assumed as variable and constant. This means that the equations represent a transformation into a co-accelerated reference system, and thus show the rest shape of the accelerated body. The observer's proper time becomes the coordinate time of the hyperbolically accelerated system, the coordinates of which are often referred to as Rindler coordinates: ${\displaystyle x}$ ${\displaystyle \eta }$ ${\displaystyle x}$ ${\displaystyle \eta }$

${\displaystyle cT=x\sinh \eta ,\quad X=x\cosh \eta ,\quad Y=y,\quad Z=z}$

Using these coordinates, for example for the analysis of the Unruh effect , gives the observer an apparent event horizon , often referred to as the Rindler horizon, which represents the limit from which the observer can no longer receive any light signals.

A more general derivation of the self-reference system (or the Fermi coordinates) for the hyperbolic movement follows by using an accompanying quadruped using Frenet-Serret formulas or rotation-free Fermi-Walker transport. Depending on the choice of the origin, metrics, time dilation between the time at the origin and the location , and the coordinate speed of light can be derived (this variable speed of light does not contradict the constancy of the speed of light in inertial systems according to SRT, since an accelerated reference system is used here, and thus this variability is a mere artifact of the coordinates used). Instead of a self-reference system defined in this way, radar coordinates can also be used, the distances being determined by light signals - in this way the expressions for metrics, time dilation and speed of light are no longer dependent on the coordinate origin used. In particular, when using radar coordinates, the coordinate speed of light is always equal to the speed of light in vacuum in inertial systems. The following table shows different coordinate systems for the hyperbolic movement (whereby the speed of light is set to 1 for simplicity): ${\displaystyle dt_{0}}$ ${\displaystyle dt}$ ${\displaystyle x}$ ${\displaystyle |dx|/|dt|}$

${\displaystyle X}$ at ${\displaystyle T=0}$	Transformation, metric, time dilation and speed of light
${\displaystyle X=0}$	Kottler-Møller coordinates
	${\displaystyle {\begin{array}{c|c}{\begin{aligned}T&=\left(x+{\frac {1}{\alpha }}\right)\sinh(\alpha t)\\X&=\left(x+{\frac {1}{\alpha }}\right)\cosh(\alpha t)-{\frac {1}{\alpha }}\\Y&=y\\Z&=z\end{aligned}}&{\begin{aligned}t&={\frac {1}{\alpha }}\operatorname {artanh} \left({\frac {T}{X+{\frac {1}{\alpha }}}}\right)\\x&={\sqrt {\left(X+{\frac {1}{\alpha }}\right)^{2}-T^{2}}}-{\frac {1}{\alpha }}\\y&=Y\\z&=Z\end{aligned}}\end{array}}}$     (2a)   ${\displaystyle ds^{2}=-(1+\alpha x){}^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}$     (2 B)   ${\displaystyle dt=(1+\alpha x)dt_{0},\qquad {\frac {|dx|}{|dt|}}=1+\alpha x}$     (2c)
	Rindler coordinates
${\displaystyle X={\frac {1}{\alpha }}}$	${\displaystyle {\begin{array}{c|c}{\begin{aligned}T&=x\sinh(\alpha t)\\X&=x\cosh(\alpha t)\\Y&=y\\Z&=z\end{aligned}}&{\begin{aligned}t&={\frac {1}{\alpha }}\operatorname {artanh} {\frac {T}{X}}\\x&={\sqrt {X^{2}-T^{2}}}\\y&=Y\\z&=Z\end{aligned}}\end{array}}}$     (2d)   ${\displaystyle ds^{2}=-(\alpha x)^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}$     (2e)   ${\displaystyle dt=\alpha x\ dt_{0},\qquad {\frac {|dx|}{|dt|}}=\alpha x}$     (2f)
	Radar coordinates (Lass coordinates)
${\displaystyle X={\frac {1}{\alpha }}}$	${\displaystyle {\begin{array}{c|c}{\begin{aligned}T&={\frac {1}{\alpha }}e^{\alpha x}\sinh(\alpha t)\\X&={\frac {1}{\alpha }}e^{\alpha x}\cosh(\alpha t)\\Y&=y\\Z&=z\end{aligned}}&{\begin{aligned}t&={\frac {1}{\alpha }}\operatorname {artanh} {\frac {T}{X}}\\x&={\frac {1}{2\alpha }}\ln \left[\alpha {}^{2}\left(X^{2}-T^{2}\right)\right]\\y&=Y\\z&=Z\end{aligned}}\end{array}}}$     (2g)
	${\displaystyle ds^{2}=e^{2\alpha x}\left(-dt^{2}+dx^{2}\right)+dy^{2}+dz^{2}}$     (2h)   ${\displaystyle dt=e^{\alpha x}dt_{0},\qquad {\frac {|dx|}{|dt|}}=1}$     (2i)

Special conformal transformation

A lesser known method of defining a frame of reference for hyperbolic movement is the special conformal transformation , which consists of an inversion, a translation and another inversion. It is usually interpreted as a gauge transformation in Minkowski spacetime, but some authors also apply it as an acceleration transformation:

${\displaystyle X^{\mu }={\frac {x^{\mu }-a^{\mu }x^{2}}{1-2ax+a^{2}x^{2}}}}$

If only one spatial dimension is used with , where can be set, and with acceleration , then follows ${\displaystyle x^{\mu }=(t,x)}$ ${\displaystyle x=0}$ ${\displaystyle a^{\mu }=(0,-\alpha /2)}$

${\displaystyle T={\frac {t}{1-{\frac {1}{4}}\alpha {}^{2}t^{2}}},\quad X={\frac {-\alpha t^{2}}{2\left(1-{\frac {1}{4}}\alpha {}^{2}t^{2}\right)}}}$

with the hyperbola . It turns out that time becomes singular, which is why one should simply avoid this limit according to Fulton & Rohrlich & Witten, whereas Kastrup (who is very critical of the acceleration interpretation) notes that this is one of the "strange" results of this interpretation. ${\displaystyle \left(X-1/\alpha \right)^{2}-T^{2}=1/\alpha ^{2}}$ ${\displaystyle t=\pm (x+2/\alpha )}$

history

Hyperbolic movement

Hermann Minkowski (1908) demonstrated the connection between the point on a world line, the norm of four acceleration, and a hyperbola of curvature. In connection with his concept of Born's rigidity, Max Born (1909) called the case with constant self-acceleration "hyperbolic motion", and gave a detailed description of moving charges. Born's formulas were supplemented and simplified by Gustav Herglotz (1909), Arnold Sommerfeld (1910) and others.

Self-reference system

Albert Einstein (1907) studied the effects in a uniformly accelerated frame of reference, and obtained the equations for coordinate-dependent time dilation and speed of light equivalent to   (2c) , and to make the formulas independent of the observer 's origin , the time dilation   (2i) in accordance with radar coordinates . Max Born (1909) used his formulas for hyperbolic movement as transformations into a "hyperbolically accelerated reference system" equivalent to   (2d) , which was continued by Arnold Sommerfeld (1910) and Max von Laue (1911) using imaginary numbers . All of this was summed up by Wolfgang Pauli (1921), who cited both   (2d) and the metric   (2e) with imaginary numbers. At the same time, Einstein (1912) studied a static gravitational field and for the first time derived the Kottler-Møller metric   (2b) and formulated approximations for   (2a) . Following Einstein, Hendrik Lorentz (1913) also received coordinates similar to   (2d) ,   (2e) and   (2f) .

Friedrich Kottler (1914) gave a detailed description , who formulated the corresponding orthonormal quadruped, the transformation formulas and metrics   (2a) ,   (2b) . Even Karl Bollert (1922), the metric received   (2b) in a study on the uniform gravitational field. In a work on Born's rigidity, Georges Lemaître (1924) received coordinates and metrics   (2a) ,   (2b) . Einstein and Nathan Rosen (1935) described   (2d) ,   (2e) as the "well-known" expressions for a homogeneous gravitational field. After Christian Møller (1943) had obtained equations   (2a) ,   (2b) in a study on homogeneous gravitational fields, he himself (1952) and Misner & Thorne & Wheeler (1973) used the equations for the Fermi-Walker to derive the same equations -Transport.

While the above studies were limited to flat Minkowski space-time, Wolfgang Rindler (1960) analyzed the hyperbolic motion in a curved space-time and showed (1966) the analogy between hyperbolic coordinates   (2d) ,   (2e) in flat space-time with Kruskal coordinates in of curved spacetime. This influences subsequent authors in their investigation of the balance radiation of an observer in hyperbolic motion, which is similar to the description of the Hawking radiation from black holes .

horizon

Born (1909) showed that the inner points of a rigid Born body in hyperbolic motion can only be in the region . Sommerfeld (1910) also defined the permitted range for the hyperbolic coordinates . Kottler (1914) helped to define the area and recognized the existence of a boundary plane beyond which no light signal can reach the observer in hyperbolic movement. Bollert (1922) called this the “horizon of the observer”. Finally, Rindler (1966) demonstrated the connection between this horizon and the horizon in Kruskal coordinates. ${\displaystyle X/\left(X^{2}-T^{2}\right)>0}$ ${\displaystyle T<X}$ ${\displaystyle X^{2}-T^{2}>0}$ ${\displaystyle c^{2}/\alpha +x}$

Radar coordinates

Using Bollert's formalism, Stjepan Mohorovičić (1922) made a different decision for some parameters and obtained the metric   (2h) with a misprint, which was corrected by Bollert (1922b) with another misprint, until Mohorovičić (1923) the formula without misprint stated. Mohorovičić was wrongly of the opinion that the Kottler-Møller metric   (2b) was wrong, which was rejected by Bollert (1922). The metric   (2h) was rediscovered by Harry Lass (1963), who also gave the corresponding coordinates   (2g) , which is why they are sometimes referred to as "Lass coordinates". The metric   (2h) as well as   (2a) ,   (2b) was also derived from Fritz Rohrlich (1963). Finally the Lass coordinates   (2g) ,   (2h) were identified by Desloge & Philpott (1987) using radar coordinates.

Table with historical formulas

Einstein (1907) ${\displaystyle {\scriptstyle {\begin{matrix}\sigma =\tau \left(1+{\frac {\gamma \xi }{c^{2}}}\right)\\\sigma =\tau e^{\gamma \xi /c^{2}}\\c\left(1+{\frac {\gamma \xi }{c^{2}}}\right)\end{matrix}}}}$ Born (1909) ${\displaystyle {\scriptstyle {\begin{matrix}x=-q\xi ,\ y=\eta ,\ z=\zeta ,\ t={\frac {p}{c^{2}}}\xi \\\left(p=x_{\tau },\ q=-t_{\tau }={\sqrt {1+p^{2}/c^{2}}}\right)\\{\boldsymbol {\downarrow }}\\x^{2}-c^{2}t^{2}=\xi ^{2}\end{matrix}}}}$ Herglotz (1909) ${\displaystyle {\scriptstyle {\begin{matrix}{\begin{aligned}x&=x'&t-z&=(t'-z')e^{\vartheta }\\y&=y'&t+z&=(t'+z')e^{-\vartheta }\end{aligned}}\\{\boldsymbol {\downarrow }}\\x=x_{0},\quad y=y_{0},\quad z={\sqrt {z_{0}^{2}+t^{2}}}\end{matrix}}}}$ Sommerfeld (1910) ${\displaystyle \scriptstyle {\begin{aligned}x&=r\cos \varphi \\y&=y'\\z&=z'\\l&=r\sin \varphi \\\varphi &=i\psi ,\ l=ict\end{aligned}}}$ by Laue (1911) ${\displaystyle \scriptstyle {\begin{matrix}\pm {\mathfrak {q}}_{x}=\pm {\frac {dx}{dt}}={\frac {cbt}{\sqrt {c^{2}+b^{2}t^{2}}}}\\\pm \left(x-x_{0}\right)={\frac {c}{b}}{\sqrt {c^{2}+b^{2}t^{2}}}\\x^{2}-c^{2}t^{2}=c^{4}/b^{2}\\\downarrow \\{\begin{aligned}X&=R\cos \varphi &R^{2}&=X^{2}+L^{2}\\L&=R\sin \varphi &\tan \varphi &={\frac {L}{X}}\end{aligned}}\end{matrix}}}$ Einstein (1912) ${\displaystyle {\scriptstyle {\begin{matrix}d\xi ^{2}-d\tau ^{2}=dx^{2}-c^{2}dt^{2}\\{\boldsymbol {\downarrow }}\\c=c_{0}+ax\\{\boldsymbol {\downarrow }}\\\xi =x+{\frac {ac}{2}}t^{2},\ \eta =y,\ \zeta =z,\ \tau =ct\end{matrix}}}}$ Kottler (1912) ${\displaystyle {\scriptstyle {\begin{aligned}x^{(1)}&=x_{0}^{(1)}&x^{(3)}&=b\cos i\varphi \\x^{(2)}&=x_{0}^{(2)}&x^{(4)}&=b\sin i\varphi \end{aligned}}}}$ Lorentz (1913) ${\displaystyle {\scriptstyle {\begin{matrix}dc={\frac {g}{c}}dz\\\hline {\begin{aligned}z&=a\left(z'-z_{0}^{\prime }\right)\\ct&=b\left(z'-z_{0}^{\prime }\right)\\a&={\frac {1}{2}}\left(e^{kt'}+e^{-kt}\right)\\b&={\frac {1}{2}}\left(e^{kt'}-e^{-kt}\right)\end{aligned}}\\{\boldsymbol {\downarrow }}\\c'=k\left(z'-z_{0}^{\prime }\right),\ z'-z_{0}^{\prime }={\frac {c^{2}}{g}}\\{\boldsymbol {\downarrow }}\\{\begin{aligned}&dx^{2}+dy^{2}+dz^{2}-c^{2}dt\\&=dx^{\prime 2}+dy^{\prime 2}+dz^{\prime 2}-c^{\prime 2}dt^{\prime 2}\end{aligned}}\end{matrix}}}}$

Kottler (1914a) ${\displaystyle {\scriptstyle {\begin{matrix}{\begin{aligned}x^{(1)}&=x_{0}^{(1)}&x^{(3)}&=b\cos iu\\x^{(2)}&=x_{0}^{(2)}&x^{(4)}&=b\sin iu\end{aligned}}\\\left(x=x_{0},\ y=y_{0},\ z={\sqrt {b^{2}+c^{2}t^{2}}}\right)\\{\boldsymbol {\downarrow }}\\ds^{2}=-c^{2}d\tau ^{2}=b^{2}(du)^{2}\\{\boldsymbol {\downarrow }}\\{\begin{matrix}c_{1}^{(1)}=0,&&c_{1}^{(2)}=0,&&c_{1}^{(3)}=-\sin iu,&&c_{1}^{(4)}=\cos iu,\\c_{2}^{(1)}=0,&&c_{2}^{(2)}=0,&&c_{2}^{(3)}=-\cos iu,&&c_{2}^{(4)}=-\sin iu,\end{matrix}}\\{\boldsymbol {\downarrow }}\\dS^{2}=(dX')^{2}+(dY')^{2}+(dZ')^{2}-\left(c+{\frac {Z'c}{b}}\right)^{2}dT'\\{\boldsymbol {\downarrow }}\\c'=c+{\frac {Z'c^{2}}{b}}\cdot {\frac {1}{c}}\end{matrix}}}}$ Kottler (1914b) ${\displaystyle \scriptstyle {\begin{matrix}{\begin{matrix}c_{1}^{(1)}=0,&&c_{1}^{(2)}=0,&&c_{1}^{(3)}={\frac {1}{i}}\sinh u,&&c_{1}^{(4)}=\cosh u,\\c_{2}^{(1)}=0,&&c_{2}^{(2)}=0,&&c_{2}^{(3)}={\frac {1}{i}}\cosh u,&&c_{2}^{(4)}=-\sinh u,\\c_{3}^{(1)}=1,&&c_{3}^{(2)}=0,&&c_{3}^{(3)}=0,&&c_{3}^{(4)}=0,\\c_{4}^{(1)}=0,&&c_{4}^{(2)}=1,&&c_{4}^{(3)}=0,&&c_{4}^{(4)}=0,\end{matrix}}\\{\boldsymbol {\downarrow }}\\X=x+\Delta ^{(2)}c_{2}+\Delta ^{(3)}c_{3}+\Delta ^{(4)}c_{4}\\{\boldsymbol {\downarrow }}\\{\begin{aligned}X&=x_{0}+{\mathfrak {X}}'\\Y&=y_{0}+{\mathfrak {Y}}'\\Z&=\left(b+{\mathfrak {Z}}'\right)\cosh {\mathfrak {u}}\\cT&=\left(b+{\mathfrak {Z}}'\right)\sinh {\mathfrak {u}}\end{aligned}}\\\left(\Delta ^{(2)}={\mathfrak {X}}',\ \Delta ^{(3)}={\mathfrak {Y}}',\ \Delta ^{(4)}={\mathfrak {Z}}'\right)\\{\boldsymbol {\downarrow }}\\{\begin{aligned}{\mathfrak {X}}'&=X_{0}-x_{0}+q_{x}T\\{\mathfrak {Y}}'&=Y_{0}-y_{0}+q_{y}T\\b+{\mathfrak {Z}}'&={\sqrt {\left(Z_{0}+q_{x}T\right)^{2}-c^{2}T^{2}}}\\c{\mathfrak {T}}'&=b\operatorname {artanh} {\frac {cT}{Z_{0}+q_{x}T}}\end{aligned}}\\\left(X=X_{0}+q_{x}T,\ Y=Y_{0}+q_{y}T,\ Z=Z_{0}+q_{x}T\right)\\{\boldsymbol {\downarrow }}\\dS^{2}=(d{\mathfrak {X}}')^{2}+(d{\mathfrak {Y}}')^{2}+(d{\mathfrak {Z}}')^{2}-c^{2}\left({\frac {b+{\mathfrak {Z}}'}{b^{2}}}\right)^{2}(d{\mathfrak {T}}')^{2}\end{matrix}}}$ Kottler (1916, 1918) ${\displaystyle \scriptstyle {\begin{matrix}{\begin{aligned}x&=x'\\y&=y'\\{\frac {c^{2}}{\gamma }}+z&=\left({\frac {c^{2}}{\gamma }}+z'\right)\cosh {\frac {\gamma t'}{c}}\\ct&=\left({\frac {c^{2}}{\gamma }}+z'\right)\sinh {\frac {\gamma t'}{c}}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=dx^{\prime 2}+dy^{\prime 2}+dz^{\prime 2}-\left(c+{\frac {\gamma }{c}}z'\right){}^{2}dt^{\prime 2}\end{matrix}}}$

Pauli (1921) ${\displaystyle \scriptstyle {\begin{matrix}{\begin{aligned}x^{1}&=\varrho \cos \varphi \\x^{4}&=\varrho \sin \varphi \end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=\left(d\xi ^{1}\right)^{2}+\left(d\xi ^{2}\right)^{2}+\left(d\xi ^{3}\right)^{2}+\left(\xi ^{1}\right)^{2}\left(d\xi ^{4}\right)^{2}\\\left(\xi ^{(1)}=\varrho ,\ \xi ^{(2)}=x^{(2)},\ \xi ^{(3)}=x^{(3)},\ \xi ^{(4)}=\varphi \right)\end{matrix}}}$ Bollert (1922) ${\displaystyle {\scriptstyle {\begin{matrix}ds^{2}=c^{2}\left(1+{\frac {\gamma _{0}x}{c^{2}}}\right)d\tau ^{2}-dx^{2}-dy^{2}-dz^{2}\\\hline ds^{2}=g_{44}dx_{4}^{2}+g_{11}dx_{1}^{2}+g_{22}\left(dx_{2}^{2}+dx_{3}^{2}\right)\\{\boldsymbol {\downarrow }}\\V''-{\frac {g_{11}}{2g_{11}}}V'=0\\\left(g_{22}=-1,\ g_{11}=-1,\ V''=0,\ V=ax+b\right)\\{\boldsymbol {\downarrow }}\\ds^{2}=dx_{4}^{2}(ax+b)^{2}-dx^{2}-dy^{2}-dz^{2}\end{matrix}}}}$ Mohorovičić (1922, 1923); Bollert (1922b) ${\displaystyle {\scriptstyle {\begin{matrix}{\text{Mohorovicic (1922):}}\\g_{11}=g_{44}=V^{2},\ VV''-V'^{2}=0,\ V\left(x_{1}\right)=e^{ax_{1}}\\{\boldsymbol {\downarrow }}\\ds^{2}=e^{2a}\left(-dx_{4}^{2}+dx_{1}^{2}\right)+dx_{2}^{2}+dx_{3}^{2}\\\\{\text{korrigiert durch Bollert (1922b):}}\\ds^{2}=e^{2ax}\left(-dx_{4}^{2}+dx_{1}^{2}\right)+dx_{2}^{2}+dx_{3}^{2}\\\\{\text{finale Korrektur durch Mohorovicic (1923):}}\\ds^{2}=e^{2ax_{1}}\left(-dx_{4}^{2}+dx_{1}^{2}\right)+dx_{2}^{2}+dx_{3}^{2}\end{matrix}}}}$ Lemaître (1924) ${\displaystyle {\scriptstyle {\begin{matrix}{\begin{aligned}1+g\xi =&(1+gx)\cosh gt\\g\tau =&(1+gx)\sinh gt\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-dx^{2}-dy^{2}-dz^{2}+(1+gx)^{2}dt^{2}\end{matrix}}}}$ Einstein & Rosen (1935) ${\displaystyle \scriptstyle {\begin{matrix}{\begin{aligned}\xi _{1}&=x_{1}\cosh \alpha x_{4}\\\xi _{2}&=x_{2}\\\xi _{3}&=x_{3}\\\xi _{4}&=x_{1}\sinh \alpha x_{4}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-dx_{1}^{2}-dx_{2}^{2}-dx_{3}^{2}+\alpha {}^{2}x_{1}^{2}dx_{4}^{2}\end{matrix}}}$ Møller (1952) ${\displaystyle \scriptstyle {\begin{matrix}\alpha _{ik}=\left({\begin{matrix}U_{4}/ic&0&0&iU_{1}/c\\0&1&0&0\\0&0&1&0\\U_{1}/ic&0&0&U_{4}/ic\end{matrix}}\right)\\U_{i}=\left(c\sinh {\frac {g\tau }{c}},\ 0,0,\ ig\cosh {\frac {g\tau }{c}}\right)\\{\boldsymbol {\downarrow }}\\X_{i}=\mathbf {f} _{i}(t)+x^{\prime \kappa }\alpha _{\kappa i}(\tau )\\{\boldsymbol {\downarrow }}\\{\begin{aligned}X&={\frac {c^{2}}{g}}\left(\cosh {\frac {gt}{c}}-1\right)+x\cosh {\frac {gt}{c}}\\Y&=y\\Z&=z\\T&={\frac {c}{g}}\sinh {\frac {gt}{c}}+x{\frac {\sinh {\frac {gt}{c}}}{c}}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=dx^{2}+dy^{2}+dz^{2}-c^{2}dt^{2}\left(1+gx/c^{2}\right)^{2}\\\\\end{matrix}}}$

Individual evidence

1. ↑ ^{a b c} Misner, CW; Thorne, KS; Wheeler, JA: Gravitation . Freeman, 1973, ISBN 0-7167-0344-0 .
2. ↑ ^{a b} Kopeikin, S., Efroimsky, M., Kaplan, G .: Relativistic Celestial Mechanics of the Solar System . John Wiley & Sons, 2011, ISBN 3-527-40856-8 .
3. ↑ Padmanabhan, T .: Gravitation: Foundations and Frontiers . Cambridge University Press, 2010, ISBN 1-139-48539-3 .
4. ^ ND Birrell, PCW Davies: Quantum Fields in Curved Space , Cambridge Monographs on Mathematical Physics. Edition, Cambridge University Press, 1982, ISBN 1-107-39281-0 .
5. ^ Leonard Susskind, James Lindesay: An Introduction to Black Holes, Information and the String Theory Revolution: The Holographic Universe . World Scientific, 2005, ISBN 981-256-131-5 , pp. 8-10.
6. ↑ Øyvind Grøn: Lecture Notes on the General Theory of Relativity , Lecture Notes in Physics. Edition, Volume 772, Springer, 2010, ISBN 0-387-88134-4 , pp. 86-91.
7. ↑ Muñoz, Gerardo; Jones, Preston: The equivalence principle, uniformly accelerated reference frames, and the uniform gravitational field . In: American Journal of Physics . 78, No. 4, 2010, pp. 377-383. arxiv : 1003.3022 . bibcode : 2010AmJPh..78..377M . doi : 10.1119 / 1.3272719 .
8. ↑ ^{a b c} David Tilbrook: General Coordinations of the Flat Space-Time of Constant Proper-acceleration . In: Australian Journal of Physics . 50, No. 5, 1997, pp. 851-868. doi : 10.1071 / P96111 .
9. ^ Jones, Preston; Wanex, Lucas F .: The Clock Paradox in a Static Homogeneous Gravitational Field . In: Foundations of Physics Letters . 19, No. 1, 2006, pp. 75-85. arxiv : physics / 0604025 . bibcode : 2006FoPhL..19 ... 75J . doi : 10.1007 / s10702-006-1850-3 .
10. ↑ Birrill & Davies (1982), pp. 110-111 or Padmanabhan (2010), p. 126 denote   (2g) ,   (2h) as Rindler coordinates; Tilbrook (1997) pp. 864-864 or Jones & Wanex (2006) also designate   (2a) ,   (2b) as Rindler coordinates
11. ↑ ^{a b c d} Rohrlich, Fritz: The principle of equivalence . In: Annals of Physics . 22, No. 2, 1963, pp. 169-191. bibcode : 1963AnPhy..22..169R . doi : 10.1016 / 0003-4916 (63) 90051-4 .
12. ↑ ^{a b} Harry Lass: Accelerating Frames of Reference and the Clock Paradox . In: American Journal of Physics . 31, No. 4, 1963, pp. 274-276. bibcode : 1963AmJPh..31..274L . doi : 10.1119 / 1.1969430 .
13. ↑ ^{a b} Rindler, W .: Hyperbolic Motion in Curved Space Time . In: Physical Review . 119, No. 6, 1960, pp. 2082-2089. bibcode : 1960PhRv..119.2082R . doi : 10.1103 / PhysRev.119.2082 .
14. ↑ ^{a b c} Rindler, W .: Kruskal Space and the Uniformly Accelerated Frame . In: American Journal of Physics . 34, No. 12, 1966, pp. 1174-1178. bibcode : 1966AmJPh..34.1174R . doi : 10.1119 / 1.1972547 .
15. ↑ von Laue, M .: Die Relativitätstheorie, Volume 1 , Fourth edition of "Das Relativitätsprinzip". Edition, Vieweg, 1921 .; First edition 1911, second 1913, third 1919.
16. ↑ ^{a b} Pauli, Wolfgang : The theory of relativity . In: Encyclopedia of Mathematical Sciences . 5, No. 2, 1921, pp. 539-776.
17. ↑ ^{a b} Møller, C .: The theory of relativity . Oxford Clarendon Press, 1955/1952.
18. ↑ PhysicsFAQ (2016), “Relativistic rocket”, see web links
19. ^ Gallant, J .: Doing Physics with Scientific Notebook: A Problem Solving Approach . John Wiley & Sons, 2012, ISBN 0-470-66597-1 , pp. 437-441.
20. ↑ Müller, T., King, A., & Adis, D .: A trip to the end of the universe and the twin "paradox" . In: American Journal of Physics . 76, No. 4, 2006, pp. 360-373. arxiv : physics / 0612126 . bibcode : 2008AmJPh..76..360M . doi : 10.1119 / 1.2830528 .
21. ^ ^{A b} Fraundorf, P .: A traveler-centered intro to kinematics . In: arxiv . 2012, pp. IV-B. arxiv : 1206.2877 . bibcode : 2012arXiv1206.2877F .
22. ^ Pauli (1921), p. 628
23. ↑ Galeriu, C .: Electric charge in hyperbolic motion: the early history . In: Archive for History of Exact Sciences . 71, No. 4, pp. 1-16. arxiv : 1509.02504 . doi : 10.1007 / s00407-017-0191-x .
24. ↑ ^{a b} Bondi, H., & Gold, T .: The field of a uniformly accelerated charge, with special reference to the problem of gravitational acceleration . In: Proceedings of the Royal Society of London . 229, No. 1178, 1955, pp. 416-424. bibcode : 1955RSPSA.229..416B . doi : 10.1098 / rspa.1955.0098 .
25. ↑ ^{a b} Fulton, Thomas; Rohrlich, Fritz: Classical radiation from a uniformly accelerated charge . In: Annals of Physics . 9, No. 4, 1960, pp. 499-517. bibcode : 1960AnPhy ... 9..499F . doi : 10.1016 / 0003-4916 (60) 90105-6 .
26. ↑ Stephen Lyle: Uniformly Accelerating Charged Particles: A Threat to the Equivalence Principle . Springer, 2008, ISBN 3-540-68477-8 .
27. ↑ Øyvind Grøn: Review Article: Electrodynamics of Radiating Charges . In: Advances in Mathematical Physics . 2012, 2012, p. 528631. doi : 10.1155 / 2012/528631 .
28. ^ Møller (1952), eq. 154
29. ↑ Misner & Thorne & Wheeler (1973), section 6.6
30. ^ Muñoz & Jones (2010), eq. 37, 38
31. ^ Pauli (1921), section 32-y
32. ↑ Rindler (1966), p. 1177
33. ^ Don Koks: Explorations in Mathematical Physics . Springer, 2006, ISBN 0-387-30943-8 , pp. 235-269.
34. ↑ Massimo Pauri, Michele Vallisneri: Märzke-Wheeler coordinates for accelerated observers in special relativity . In: Foundations of Physics Letters . 13, No. 5, 2000, pp. 401-425. arxiv : gr-qc / 0006095 . doi : 10.1023 / A: 1007861914639 .
35. ↑ Dolby, Carl E .; Gull, Stephen F .: On radar time and the twin "paradox" . In: American Journal of Physics . 69, No. 12, 2001, pp. 1257-1261. arxiv : gr-qc / 0104077 . bibcode : 2001AmJPh..69.1257D . doi : 10.1119 / 1.1407254 .
36. ↑ ^{a b} Minguzzi, E .: The Minkowski metric in non-inertial observer radar coordinates . In: American Journal of Physics . 73, 2005, pp. 1117-1121. arxiv : physics / 0412024 . bibcode : 2005AmJPh..73.1117M . doi : 10.1119 / 1.2060716 .
37. ↑ ^{a b} Kastrup, HA: On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics . In: Annals of Physics . 520, No. 9-10, 2008, pp. 631-690. arxiv : 0808.2730 . bibcode : 2008AnP ... 520..631K . doi : 10.1002 / andp.200810324 .
38. ^ ^{A b} Fulton, T., Rohrlich, F., & Witten, L .: Physical consequences of a co-ordinate transformation to a uniformly accelerating frame . In: Il Nuovo Cimento . 26, No. 4, 1962, pp. 652-671. bibcode : 1962NCim ... 26..652F . doi : 10.1007 / BF02781794 .
39. ↑ Blum, AS, Renn, J., Salisbury, DC, Schemmel, M., & Sundermeyer, K .: 1912: A turning point on Einstein's way to general relativity . In: Annals of Physics . 524, No. 1, 2012, pp. A12-A13. bibcode : 2012AnP ... 524A..11B . doi : 10.1002 / andp.201100705 .
40. ↑ Desloge, Edward A .; Philpott, RJ: Uniformly accelerated reference frames in special relativity . In: American Journal of Physics . 55, No. 3, 1987, pp. 252-261. bibcode : 1987AmJPh..55..252D . doi : 10.1119 / 1.15197 .
41. ↑ Herglotz (1909), pp. 408, 414

Historical sources

1. ↑ ^{a b} Einstein, Albert: About the principle of relativity and the conclusions drawn from it . In: Yearbook of radioactivity and electronics . 4, pp. 411-462. bibcode : 1908JRE ..... 4..411E . Einstein, Albert: Speed ​​of light and statics of the gravitational field . In: Annals of Physics . 343, No. 343, 1912, pp. 355-369.
2. ↑ ^{a b} Born, Max: The theory of the rigid electron in the kinematics of the principle of relativity . In: Annals of Physics . 335, No. 11, 1909, pp. 1-56. bibcode : 1909AnP ... 335 .... 1B . doi : 10.1002 / andp.19093351102 .
3. ↑ ^{a b c} Herglotz, Gustav: About the body to be called rigid from the standpoint of the principle of relativity . In: Annals of Physics . 336, No. 2, pp. 393-415. bibcode : 1910AnP ... 336..393H . doi : 10.1002 / andp.19103360208 .
4. ↑ ^{a b c d e} Sommerfeld, Arnold: On the theory of relativity II: Four-dimensional vector analysis . In: Annals of Physics . 338, No. 14, 1910, pp. 649-689. bibcode : 1910AnP ... 338..649S . doi : 10.1002 / andp.19103381402 .
5. ↑ ^{a b c} Laue, Max von: The principle of relativity . Vieweg, Braunschweig 1911.
6. ↑ Lorentz, Hendrik Antoon: The principle of relativity. Three lectures given at Teyler's Foundation in Haarlem (1913) . BG Teubner, Leipzig / Berlin 1914/1913.
7. ↑ Kottler, Friedrich: About the space-time lines of the Minkowski world . In: Vienna meeting reports 2a . 121, 1912, pp. 1659-1759. Kottler, Friedrich: Relativity Principle and Accelerated Movement . In: Annals of Physics . 349, No. 13, 1914, pp. 701-748. bibcode : 1914AnP ... 349..701K . doi : 10.1002 / andp.19143491303 . Kottler, Friedrich: Falling reference systems from the standpoint of the principle of relativity . In: Annals of Physics . 350, No. 20, 1914, pp. 481-516. bibcode : 1914AnP ... 350..481K . doi : 10.1002 / andp.19143502003 . Kottler, Friedrich: About Einstein's equivalence hypothesis and gravitation . In: Annals of Physics . 355, No. 16, 1916, pp. 955-972. bibcode : 1916AnP ... 355..955K . doi : 10.1002 / andp.19163551605 . Kottler, Friedrich: About the physical foundations of Einstein's theory of relativity . In: Annals of Physics . 361, No. 14, 1918, pp. 401-461. bibcode : 1918AnP ... 361..401K . doi : 10.1002 / andp.19183611402 .
8. ↑ ^{a b} Pauli, W .: The theory of relativity . In: Encyclopedia of Mathematical Sciences , Volume 5.2 1921, pp. 539-776. New edition 2013: Editor: Domenico Giulini, Springer, 2013, ISBN 3-642-58355-5 .
9. ↑ Karl Bollert: The homogeneous gravitational field and the Lorentz transformations . In: Journal of Physics . 10, No. 1, 1922, pp. 256-266. bibcode : 1922ZPhy ... 10..256B . doi : 10.1007 / BF01332567 . Karl Bollert: The origin of the Lorentz shortening and the strict treatment of the clock paradox . In: Journal of Physics . 12, No. 1, 1922, pp. 189-206. bibcode : 1923ZPhy ... 12..189B . doi : 10.1007 / BF01328090 .
10. ↑ Mohorovičić, S .: The "homogeneous" gravitational field and the Lorentz transformation . In: Journal of Physics . 11, No. 1, 1922, pp. 88-92. bibcode : 1922ZPhy ... 11 ... 88M . doi : 10.1007 / BF01328404 . Mohorovičić, S .: Ether, Matter, Gravitation and Theory of Relativity . In: Journal of Physics . 18, No. 1, 1923, pp. 34-63. bibcode : 1923ZPhy ... 18 ... 34M . doi : 10.1007 / BF01327684 .
11. ↑ Lemaître, G .: The motion of a rigid solid according to the relativity principle . In: Philosophical Magazine Series 6 . 48, No. 283, 1924, pp. 164-176. doi : 10.1080 / 14786442408634478 .
12. ↑ ^{a b} Møller, C .: On homogeneous gravitational fields in the general theory of relativity and the clock paradox . In: Dan. Mat. Fys. Medd. . 8, 1943, pp. 3-25. Møller, C .: The theory of relativity . Oxford Clarendon Press, 1955/1952.
13. ↑ Sommerfeld (1910), pp. 670-671.
14. ↑ Kottler (1914b), pp. 488-489, 492-493
15. ^ Minkowski, Hermann: space and time . Paper presented at the 80th Congress of Scientists of Cologne on 21 September 1908 . In: Annual report of the German Mathematicians Association . , Leipzig 1909.
16. ↑ Einstein, Albert & Rosen, Nathan: A Particle Problem in the General Theory of Relativity . In: Physical Review . 48, 1935, p. 73. bibcode : 1935PhRv ... 48 ... 73E . doi : 10.1103 / PhysRev.48.73 .
17. ↑ ^{a b} Born (1909), p. 25th
18. ↑ ^{a b} Sommerfeld (1910), pp. 670-671
19. ↑ ^{a b} Einstein (1912), pp. 358-359
20. ↑ ^{a b} Lorentz (1913), pp. 34-38; 50-52
21. ↑ Kottler (1912), pp. 1715; Kottler (1914a), Table I; pp. 747-748; Kottler (1914b), pp. 488-489, 503; Kottler (1916), pp. 958-959; (1918), pp. 453-454;
22. ↑ ^{a b} Bollert (1922a), p. 261, 266
23. ↑ ^{a b} Lemaitre (1921), pp. 166, 168
24. ↑ ^{a b} Einstein & Rosen (1935), p. 74
25. ↑ ^{a b} Møller (1952), pp. 121-123; 255-258
26. ^ Born (1909), p. 35
27. ↑ Sommerfeld (1910), p. 672
28. ↑ Kottler (1914), pp. 489-490
29. ↑ Bollert (1922b), pp. 194-196
30. ^ ^{A b} Mohorovičić (1922), p. 92, without in the exponent due to printing errors, corrected by Bollert (1922b), p. 189 and fully by Mohorovičić (1923), p. 54 ${\displaystyle x_{1}}$
31. ↑ Bollert (1922b), p. 189
32. ↑ Einstein (1907), §§ 18-21
33. ↑ von Laue (1911), p. 109
34. ↑ Kottler (1912), pp. 1715
35. ↑ Kottler (1914a), Table I; pp. 747-748
36. ↑ Kottler (1914b), pp. 488-489, 503
37. ↑ Kottler (1916), pp. 958-959; (1918), pp. 453-454
38. ^ Pauli (1921), pp. 647-648

Web links

• Physics FAQ: The Relativistic Rocket
• Mathpages: Accelerated Travels , Does A Uniformly Accelerating Charge Radiate?