Minkowski diagram
The Minkowski diagram was developed by Hermann Minkowski in 1908 and is used to illustrate the properties of space and time in the special theory of relativity . It allows a quantitative understanding of the associated phenomena such as time dilation and length contraction without formulas .
The Minkowski diagram is a space-time diagram with only one space dimension . A superimposition of the coordinate systems for two observers moving against each other at constant speed is shown so that for the location and time coordinates x and t, which one observer uses to describe what is happening, those of the other x ' and t' can be read directly and vice versa. From this graphically one-to-one assignment of x and t to x ' and t' , the consistency of numerous apparently paradoxical statements of the theory of relativity becomes immediately apparent. The insurmountability of the speed of light is graphically revealed as a consequence of the properties of space and time. The shape of the diagram follows directly and without formulas from the postulates of the special theory of relativity and illustrates the close relationship between space and time that emerges from the theory of relativity. An extension is the Penrose diagram , with which the global structure of more general , also curved , spacetime can be represented.
Basics
In favor of representability, Minkowski diagrams dispense with two of the three spatial dimensions and only consider what happens in a one-dimensional world. In contrast to the usual path-time diagrams, the path is shown on the x- axis and the time on the y- axis . This means that the events can be mapped directly into the diagram on a horizontal path, with this path moving from bottom to top through the diagram as time passes. Every object on this path, such as an observer or a vehicle, describes a line in the diagram that is called its world line .
Each point in this diagram marks a certain point in space and time. Such a point is referred to as an event regardless of whether anything happens at this time and in this place.
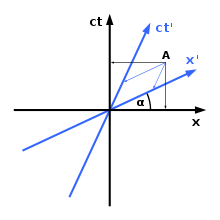
It has proven to be advantageous not to plot the time t directly on the time axis , but rather the assigned variable ct , where c = 299792.458 km / s denotes the speed of light . In this way, one second corresponds to a section of 299792.458 km on the ordinate. Because x = ct for a light particle that passes the coordinate origin to the right, its world line is a straight line inclined by 45 ° in the diagram, provided that the same scale is selected for both coordinate axes.
Path-time diagram in Newtonian physics
The diagram on the right shows the coordinate system of an observer, who for the sake of simplicity we will call the one at rest, and who is located at x = 0. The world line of the observer is therefore identical to the time axis. Any parallel to this axis would correspond to a likewise stationary object in a different place. The blue straight line, on the other hand, corresponds to an object that is moving to the right at constant speed, for example a moving observer.
This blue straight line can now be interpreted as the time axis of this observer, which together with the spatial axis, which is identical for both observers, represents his coordinate system. This corresponds to an agreement between the two observers to denote the point x = 0 and t = 0 also with x ′ = 0 and t ′ = 0. The coordinate system of the moving observer is skewed. To read off the coordinates of a point, in this case the two parallels are formed by the point of occurrence to the axes and their intersection with the axes is considered.
The example of event A in the diagram shows that, as expected, different values are determined for the location coordinate, since the moving observer has moved towards the location of the event since t = 0. On the other hand, in Newtonian physics an event takes place at the same point in time from the point of view of both observers. The scale on the time axis of the moving observer is therefore stretched in such a way that the same values are at the same height above the x axis on both time axes.
In general, all events that are parallel to the path axis take place simultaneously for both observers. There is only one universal time t = t ′ , which manifests itself in the existence of a common path axis. Analogously, the existence of two different time axes is related to the fact that both observers determine different spatial coordinates. This graphical translation of the coordinates x and t into x ' and t' or vice versa takes place mathematically via the Galilei transformation .
Minkowski diagram in special relativity
Albert Einstein (1905) discovered that the Newtonian description does not correspond to reality. The higher the observed speeds, the greater the deviations. Space and time are such that different rules apply to the translation of the coordinates between moving observers. In particular, events that one observer assesses as simultaneous take place at different times for the other observer who is moving relative to him. This relativity of simultaneity was elegantly illustrated by Hermann Minkowski .
In the Minkowski diagram, the relativity of the simultaneity corresponds to the existence of different path axes for the two observers. According to the above rule, every observer interprets all events on a straight line parallel to his path axis as simultaneous. The sequence of events from the point of view of a specific observer can thus be traced graphically by parallel shifting such a straight line from bottom to top.
If ct is plotted instead of t on the time axis, the angle α between the two path axes turns out to be identical to that between the two time axes. The principle of the constancy of the speed of light can be interpreted as the reason for this orientation of the path axes (see below). The angle α results from the relative speed v zu
- .
The associated translation of the coordinates x and t into x ' and t' or vice versa is mathematically carried out using the Lorentz transformation . The axes are scaled as follows: If U is the selected graphic length of the length unit used (e.g. 1 Ls = 1 light second ) on the ct and x axes, we mark these two axes as usual at the graphic distance U from Origin with a 1 (in the adjacent graphic U ). The graphic distance U ′ from the origin, at which the first marking is made on the ct ′ and x ′ axes, then results in:
- .
Explanation: If the ct axis represents the world line of a clock at rest in S , then U corresponds to the duration multiplied by c between two events occurring on this world line, which is called the proper time of the clock. The length U on the x- axis corresponds to the rest length or proper length of a scale at rest in S. The same relationships also apply to the distances U ′ on the ct ′ and x ′ axes. The first marking on the ct ′ axis has the mathematical coordinates ( x ′, ct ′ ) = (0,1) in the system S ′ and the first marking on the x ′ axis has the mathematical coordinates ( x ′, ct ′ ) = (1.0). In the unprimed coordinate system S , the Lorentz transformation results in the first marking on the ct ′ axis having the mathematical coordinates ( x, ct ) = ( γ v / c, γ ). Since the unprimed coordinate system is graphically a Cartesian coordinate system, the graphical distance of the marking results from the Pythagorean theorem and simplification to the formula given above:
The same result is obtained when looking at the x ' axis.
Symmetrical Minkowski diagram
If only two inertial systems are considered, the different scaling on the axes can be avoided and a symmetrical representation can be achieved. Because between two relatively moving inertial systems there is always a third one, in which the other two move in opposite directions at the same speed (“middle system”). If and between two inertial systems and are given, then they are related to the corresponding quantities in the mean system as follows:
If, for example, there is between S and S ' , then according to (2) they move in their mean system with approximately ± 0.268 c in each opposite direction. Or if in is given, then according to (1) the relative velocity between S and S ′ in their own rest systems is given as 0.8 c. The construction of the oppositely directed axes of S and S ′ then takes place according to the usual method with reference to the orthogonal axes of the central system (see Figure 1).
It turns out, however, that the construction of these symmetrical Minkowski diagrams can be significantly simplified, whereby neither the mean system nor have to be listed, but only between S and S ′ : If the angle is between the ct ′ and ct axes (and between the x - and x ′ axes), and between the x ′ and ct ′ axes, then we get:
This results in the following two construction methods (Fig. 2): The x -axis is first drawn perpendicular to the ct ' -axis, then the x' and ct -axes are added at an angle ; or the x ' -axis is drawn at an angle with respect to the ct' -axis, then the x -axis perpendicular to the ct ' -axis and the ct -axis perpendicular to the x' -axis. Additionally (Fig. 3) it follows that the parallel projections of vector correspond to its contravariant components (x, t; x ′, t ′) , and the orthogonal projections to its covariant components.
history
- Max Born (1920) used in his book Einstein's Theory of Relativity different Minkowski diagrams with two mutually perpendicular rays of light as an axis cross. In order to show the symmetry of length contraction and time dilation, he added the axes of two systems S and S ′ , with the x axis being approximately perpendicular to the ct ′ axis and the x ′ axis approximately perpendicular to the ct axis.
- Dmitry Mirimanoff (1921) discovered the existence of “middle systems” that can always be found in relation to two inertial systems moving relative to one another. However, he showed no graphical interpretation of this relationship.
- Paul Gruner (1921) developed symmetrical diagrams in a systematic way together with Josef Sauter. Relativistic effects such as length contraction and time dilation were derived as well as the connection between contravariant and covariant components. Gruner expanded this method in further work (1922-1924) and paid tribute to Mirimanoff's work.
- The construction of such symmetrical diagrams was rediscovered several times later. For example, Enrique Loedel Palumbo published several works in Spanish beginning in 1948, in which he developed this method. In 1955 it was rediscovered again by Henri Amar . In some textbooks, such diagrams are therefore referred to as "Loedel diagrams".
Time dilation
The so-called time dilation means that a clock that shows its own time and moves relative to an observer, runs slower with regard to whose coordinate time, and thus also the time in this system itself. This fact can be read off directly from the Minkowski diagram opposite. The observer moves within space-time from the origin O in direction A and the clock from O in direction B. All events that this observer interprets as simultaneous at A lie on the parallel to his path axis, i.e. the straight line through A and B. Because of OB < OA , however, a smaller amount of time has passed on the clock that is moved relative to it than on the clock that the observer is carrying.
A second observer who has moved from O to B with one clock will, however, claim that the other clock is only at C at this moment and that it is therefore the one that is running slower. The different interpretations of what is happening at the same time in another place is the cause of this seemingly paradoxical situation. In view of the principle of relativity, the question of who is correctly assessing the situation cannot be answered in principle and is therefore pointless.
Length contraction
The so-called length contraction means that a length scale of a certain rest length , which moves relative to an observer, is measured as shortened with his scale, and thus also the space in this system itself. The observer moves again on the ct axis. The world lines of the two end points of a scale moved relative to it move along the ct ′ axis and parallel to it through A and B. For the observer, the scale at time t = 0 only extends from O to A. For one along the ct ′ -Axis, the second observer, for whom the scale is at rest, has the rest length OB at the moment t ′ = 0. To the first observer it appears shortened because of OA < OB .
The observer who was moving along will object that the first observer recorded the start and end points at O and A and thus not at all at the same time, so that he determined a wrong length due to his interim movement. Using the same line of argument, the second observer determines a length contraction from OD to OC for the length of a rule whose end points move along the ct axis and parallel to it through C and D. The apparently paradoxical situation that each other's standards are measured as abbreviated is based on the relativity of simultaneity, as the Minkowski diagram shows.
In all of these considerations it was assumed that the observers take into account the known propagation speed of the light in their statements . This means that they do not state what they see immediately, but what they consider to be real based on the signal propagation time and the spatial distance they have determined to the events seen.
Principle of the constancy of the speed of light
The more important of the two postulates of the special theory of relativity is the principle of the constancy of the speed of light . It says that the vacuum speed of light has the same value c in every inertial system , regardless of the speed of the light transmitter or the light receiver. All observers who measure the speed of light come to the same result, regardless of their own state of motion. This statement appears paradoxical at first, but is graphically derived directly from the Minkowski diagram. It also explains the result of the Michelson-Morley experiment , which caused astonishment before the theory of relativity was discovered.
For world lines of two light particles that pass the origin in different directions, x = ct and x = - ct, that is, each point on the path corresponds to sections of the same amount on the x and ct axes. From the rule for reading coordinates in an oblique coordinate system, it follows that these world lines are the two bisectors of the x and ct axes. The Minkowski diagram shows that they are also the bisectors of the x ' and ct' axes. This means that both observers determine the same value c for the absolute value of the speed of these two light particles .
In principle, further coordinate systems can be added to this Minkowski diagram for observers at any speed. In all of these coordinate systems, the world lines of light particles form the bisectors of the coordinate axes. The closer the relative speeds approach the speed of light, the more the coordinate axes of at least one of the systems involved cling to the bisector. The path axes are always flatter than these bisectors and the time axes are always steeper. The scales on the respective path and time axes are always the same, but generally differ from those of the other coordinate systems.
Speed of light and causality
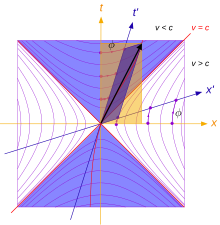
All straight lines through the origin that are steeper than the two world lines of the light particles correspond to objects that move more slowly than the speed of light . Since the world lines of the light particles are identical for all observers, this statement applies regardless of the observer. From the origin, every point above and between the world lines of the two light particles can be reached with less than the speed of light, so that every corresponding event can have a cause-effect relationship with the origin. This area is called the absolute future , since every event there, regardless of the observer, takes place later than the event that marks the origin, of which one can easily convince oneself graphically.
Analogously, the area below the origin and between the world lines of the two light particles is the absolute past with respect to the origin. Every event there can be the cause of an effect at the origin and is clearly in the past.
The relationship between two event points, which in this way can be in a cause-effect relationship, is also referred to as time-like , since they have a finite time interval for all observers. In contrast, the connecting route always represents the time axis of a possible coordinate system, for whose observers the two events take place at the same place. If two events can be connected with the speed of light, they are called light-like .
Two event points, which can in no way have a cause-effect relationship, as they can only be connected with faster than light speed, have no generally defined temporal relationship to one another, rather one or the other is earlier or both are at the same time, depending on the observer. On the other hand, they cannot take place in the same place (at different times) for any observer (absolutely elsewhere), so they have a spatial relationship to one another.
In principle, a further spatial dimension can be added to the Minkowski diagram , so that a three-dimensional representation is created. In this case, the areas of the past and future become cones , the tips of which touch at the origin. They are known as cones of light .
Speed of light as a limit
Analogously, all straight lines through the origin that are flatter than the two world lines of the light particles would correspond to objects or signals that move faster than light , and with the above argument again independent of the observer. This means that no contact can be established between all events outside the light cone and that at the origin itself at the speed of light. The ratio of two such event points is also referred to as space-like , since they are at a finite distance for all observers. In contrast, the connecting route always represents the path axis of a possible coordinate system, for whose observers the two events take place simultaneously. By slightly varying the speed of this coordinate system in both directions, two coordinate systems can therefore always be found whose observers assess the chronological order of these two events differently.
Based on the postulate of the constant speed of light, superluminal speed would mean that for every observer for whom such an object would move from X to Y , another could be found for whom it would move from Y to X , again without the Ask who correctly describes the situation, makes sense. This would violate the principle of causality .
In addition, it follows from the theory of relativity that signals that are faster than light can be used to send information into one's own past. In the diagram opposite, the observer in the x - ct system sends a message from O to A at faster than light speed . At point A , it is received by an observer in the x ' - ct' system, who in turn sends back a response signal at faster than light speed so that it in B and in the past by O arrives. The absurdity of the process is made clear by the fact that both observers would then have to claim to have received the reply to their message before it was sent.
The incompatibility of the theory of relativity and the possibility of accelerating an observer to the speed of light or even beyond is also expressed in the fact that at the speed of light his time and path axis would coincide with the bisector, so that the coordinate system as such would collapse.
These considerations show graphically using the Minkowski diagram that the insurmountable speed of light is a consequence of the relativistic structure of space and time and not a property of things, such as a merely imperfect spaceship.
The relationship between space and time
In the basic equations of the theory of relativity, space and time appear to be largely equivalent and can therefore be combined to form a four-dimensional space - time . This close relationship between space and time is also shown in the Minkowski diagram.
The well-known equivalence of the three dimensions of space expresses itself in particular in the possibility of rotating in space. The three dimensions are therefore not fixed, but can be freely selected by defining a coordinate system. In contrast, space and time appear strictly separate in Newtonian physics. In the special theory of relativity, however, relative movements prove to be closely related to rotations of coordinate systems with space and time axes in space-time: Since the angle between the two space and the two time axes is the same in the symmetrical representation, the x- axis is perpendicular the ct ' -axis and also the x' -axis on the ct -axis. The arrangement of the four axes is thus identical to that of two normal right-angled coordinate systems that were merely rotated by the angle φ with respect to one another, with the two time axes subsequently being interchanged. This results in a shear of the axes instead of a rotation. This swapping of two axes and all the differences between space and time can ultimately be traced back to a single sign in the equation that links space and time by defining the metric of space-time.
For this reason, the importance of the speed of light as a fundamental natural constant in physics is primarily to establish this connection between space and time. The fact that photons move with this speed is to be seen as a consequence of this close relationship. In the theory of relativity it is therefore also common to calculate with x 1 to x 4 instead of the coordinates x, y, z and t , where x 4 = ct. This simplifies all formulas considerably, and a dimensionless number c = 1 results for the speed of light in these units .
See also
Individual evidence
- ↑ Albert Einstein: On the electrodynamics of moving bodies . In: Annals of Physics . 322, No. 10, 1905, pp. 891-921.
- ^ Hermann Minkowski: Space and Time . Lecture given at the 80th meeting of natural scientists in Cologne on September 21, 1908 . In: Annual report of the German Mathematicians Association 1909.
- ↑ Jürgen Freund: Special theory of relativity for first-year students . vdf Hochschulverlag, 2007, ISBN 3-8252-2884-3 , p. 39.
- ↑ a b Dmitry Mirimanoff: La transformation de Lorentz-Einstein et le temps universel de M. Ed. Guillaume . In: Archives des sciences physiques et naturelles (supplement) . 3, 1921, pp. 46-48.
- ↑ Albert Shadowitz: The Electromagnetic Field , Reprint of 1975 edition. Edition, Courier Dover Publications, 2012, ISBN 0-486-13201-3 , p. 460. See limited preview in Google Book Search.
- ↑ a b Leo Sartori: Understanding Relativity: a simplified approach to Einstein's theories . University of California Press, 1996, ISBN 0-520-20029-2 , p. 151 ff.
- ^ A b Paul Gruner, Josef Sauter: Representation géométrique élémentaire des formules de la théorie de la relativité . In: Archives des sciences physiques et naturelles . 3, 1921, pp. 295-296.
- ↑ a b Paul Gruner: An elementary geometric representation of the transformation formulas of the special theory of relativity . In: Physikalische Zeitschrift . 22, 1921, pp. 384-385.
-
↑ Max Born: Einstein's theory of relativity , first edition. Edition, Springer, Berlin 1920, pp. 177–180. 7th edition: Max Born: Einstein's theory of relativity . Springer, Berlin-Heidelberg-New York 1964/2003, ISBN 3-540-00470-X , pp. 212-216.
- ^ Paul Gruner: Elements of the theory of relativity . P. Haupt, Bern 1922.
- ↑ Paul Gruner: Graphical representation of special relativity theory in four-dimensional space-time world I . In: Journal of Physics . 10, No. 1, 1922, pp. 22-37. doi : 10.1007 / BF01332542 .
- ↑ Paul Gruner: Graphic representation of the special theory of relativity in the four-dimensional space-time world II . In: Journal of Physics . 10, No. 1, 1922, pp. 227-235. doi : 10.1007 / BF01332563 .
- ^ Paul Gruner: a) Représentation graphique de l'univers espace-temps à quatre dimensions. b) Representation of the graphique du temps universel dans la théorie de la relativité . In: Archives des sciences physiques et naturelles . 4, 1921, pp. 234-236.
- ↑ Paul Gruner: The meaning of “reduced” orthogonal coordinate systems for tensor analysis and the special theory of relativity . In: Journal of Physics . 10, No. 1, 1922, pp. 236-242. doi : 10.1007 / BF01332564 .
- ↑ Paul Gruner: Geometric representations of the special theory of relativity, especially the electromagnetic field of moving bodies . In: Journal of Physics . 21, No. 1, 1924, pp. 366-371. doi : 10.1007 / BF01328285 .
- ↑ Enrique Loedel: Aberracion y Relatividad . In: Anales Sociedad Científica Argentina . 145, 1948, pp. 3-13.
- ^ Fisica relativista. Kapelusz Editorial, Buenos Aires, Argentina (1955).
- ^ Henri Amar: New Geometric Representation of the Lorentz Transformation . In: American Journal of Physics . 23, No. 8, 1955, pp. 487-489. doi : 10.1119 / 1.1934074 .
- ^ Henri Amar, Enrique Loedel: Geometric Representation of the Lorentz Transformation . In: American Journal of Physics . 25, No. 5, 1957, pp. 326-327. doi : 10.1119 / 1.1934453 .
- ↑ Albert Shadowitz: Special relativity , Reprint edition of the 1968th Edition, Courier Dover Publications, 1988, ISBN 0-486-65743-4 , pp. 20-22.