Machscher cone
The Mach cone is a shock wave which in waves occurs with high speeds. It was named after Ernst Mach .
An object moving at the same speed compresses the medium in front of it, the sound waves triggered by it propagate spherically at the speed of sound . However, if the object itself moves at supersonic speed , i.e. faster than the speed of propagation of the waves, then the compression front can never detach itself from the object in the direction of movement of the object and thus runs permanently ahead of it. The shock waves that are triggered form, as shown by the superposition of elementary waves according to Huygens' principle , to form a stationary cone surface in the reference system of the moving object. Half the apex angle of this cone is called Mach's angle .
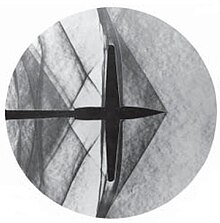
Visible Machscher cone
When the air humidity is high, the collision front of the Mach cone becomes visible as a cloud disk . Immediately after compression, a similarly strong negative pressure follows in the cone. As a result of this adiabatic expansion , the partial pressure of the water clearly exceeds the saturation vapor pressure . As a result, water vapor condenses into small droplets that are visible as a wall of smoke. Behind the collision front, the air pressure normalizes, the droplets evaporate and the fog dissolves. It creates the impression of a cloud disk attached to the aircraft .
With Schlieren optics , Mach cones can be displayed and measured in the wind tunnel .
Mathematical description
Opening angle of the Mach cone
The equation for half the opening angle of the Mach cone is:
- : distance covered in time
- : machsch angle
- : Speed of sound
- : Airspeed of the object
- : Mach number
At the speed of sound, the cone opening angle is 180 °. In this case, the cone has taken the form of a flat impact front. For the penetrating spherical wave fronts form cones with constructive interference.
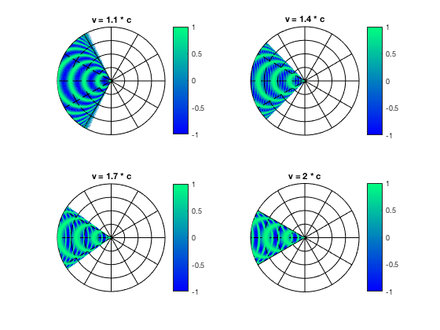
Description of dynamic wave patterns
- : Speed of sound
- : Frequency of the sound source
- : Angular frequency of the sound source
- : Wavelength
- : Speed of the aircraft
- : Wave propagation constant
- : Azimuthal angle ( polar coordinates )

Description of the wavefront as a shifted circle parameterization :
Here, a free parameter corresponds to which is located in the interval , but is not the same as the typical azimuthal angle of rotation of the polar coordinates. The geometric derivation can be seen in the figure "Graphical representation of the wavelength vector".
The angle-dependent wavelength is the norm of this circular parameterization:
The wave propagation constant can be given as follows:
The azimuthal angle of revolution is calculated from the components of the wavelength vector as a function of:
An effective conversion of the azimuthal angle into the parameter angle is given by the following formula in determinant notation:
The wave equation can thus be described as a parameterized surface as follows:
The parameter corresponds to the radial parameter of the polar coordinates. The animation shown above is based on this calculation principle. With a Mach number of 2, the opening angle of the cone is exactly 30 °.
See also
Web links
- Sonic Bang - Astronomy Picture of the Day of August 19, 2007.
- The Ares-1-X rocket takes off - Astronomy Picture of the Day of November 2, 2009.
- Shuttle breaks sound barrier ( Memento from January 28, 2018 in the Internet Archive )
- NASA: Mach Angel , website with description of the Mach cone.
Individual evidence
- ↑ Supersonic wind tunnel with Schlieren optics ( Memento from January 1, 2014 in the Internet Archive ) (PDF file; 182 kB)


















![{\ displaystyle {\ overrightarrow {\ lambda}} (\ alpha) = {\ begin {pmatrix} \ lambda _ {x} (\ alpha) \\\ lambda _ {y} (\ alpha) \ end {pmatrix}} = {\ begin {pmatrix} {\ frac {c_ {s}} {f_ {s}}} \ cos (\ alpha) - {\ frac {v_ {x}} {f_ {s}}} \\ {\ frac {c_ {s}} {f_ {s}}} \ sin (\ alpha) - {\ frac {v_ {y}} {f_ {s}}} \ end {pmatrix}} \ quad \ quad \ alpha \ in [- \ pi, \ pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372abdc12127288d304d59eb3acfaf4fa23d5434)

![{\ displaystyle [- \ pi, \ pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)