Marching cubes
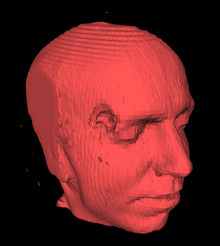
Marching Cubes is an algorithm for displaying isosurfaces in 3D computer graphics . It approximates an isosurface using a polygon graphic .
Development of the algorithm
Marching Cubes was introduced in 1987 by William E. Lorensen and Harvey E. Cline as the result of research for the research division of General Electric in the journal Computer Graphics . Lorensen and Cline dealt with the efficient visualization of image data from imaging processes such as computed tomography , magnetic resonance tomography and single-photon emission computed tomography .
Importance of the algorithm
There are various methods of modeling three-dimensional objects in 3D computer graphics . One of them is the modeling as a polygonal surface (" wire frame model "): You add angular surfaces - usually triangles - to one another in such a way that they reproduce the surface of the object. These models can be converted into pictures very quickly and easily, the memory requirement of a model is relatively low and very realistic pictures are possible thanks to numerous refinements. On the other hand, it is almost impossible to model a medium like fog that does not have a clearly defined surface in this way .
Another method is modeling as a voxel data set: the density of the material is read off at regular intervals at a single point on the object ; the result is a cube-shaped three-dimensional grid of voxels. Imaging systems such as computed tomography naturally generate such models. These voxel models can be converted into images quite easily, which also appear very realistic and true to detail. However, the model requires a great deal of storage space - ranging in size from several hundred megabytes to a few gigabytes - and the visualization takes considerably longer than with a polygonal surface model of comparable size. In addition, manipulations (e.g. deforming an object) are much more difficult, sometimes even impossible.
Marching Cubes made it possible for the first time to approximate impractical volume models with practicable polygonal surface models in order to then visualize them efficiently. The algorithm thus satisfied the desire of radiology for a method to display data from imaging systems such as computer tomography quickly and clearly. Even today, Marching Cubes is still in use as an efficient transformation algorithm. Volume graphics have made progress in the meantime and have found their way into computer graphics practice through 3D textures , but so far there is no hardware that accelerates volume graphics in the same way as graphics processors do with triangles.
The algorithm
The idea of Marching Cubes is the given voxel model of an object first in small cubes ( cubes to break down) and then and to determine from a cube "march" to the next, such as the surface of the object by intersecting the respective cube. To do this, a user-selected threshold is used to determine which parts of each cube are inside and which are outside the ultimate object. By changing this limit value, interpreted as “density”, the user can determine which areas of the object are displayed and which are not.
input
The algorithm processes the following input parameters:
- Voxel graphic. The volume model of the object.
- Format: Usually a voxel graphic is available as a list L of two-dimensional arrays A i - called “slices”. The following applies: L (i) = A i , furthermore A z [x, y] = ρ x, y, z ∈ [0,1] is the density value of the modeled object at the point (x, y, z).
- Density value ρ. This parameter controls which areas of the model are interpreted as solid and which as transparent.
- Format: ρ ∈ [0,1].
Data structures
The following data structures are used or generated by the algorithm, but are not passed as input parameters:
- Triangle Lookup Table (TLT). There are 256 ways in which a surface of any shape can divide a marching cube into indoor and outdoor areas; because according to combinatorics there are 2 8 = 256 possibilities to divide the 8 corners of a marching cube into 2 quantities “inside” and “outside”. The Triangle Lookup Table contains all of these possibilities; Due to the symmetry of the cases, there are actually only 15 different entries.
- Format: TLT (i) = v 1 , v 2 , v 3 ,…, for the case i, TLT (i) provides a list of all triangles required, each consisting of three nodes.
- D. Here the algorithm creates a list of all triangles that are required to approximate the entered voxel graphic with a polygon graphic.
- N. In addition to the triangle list, the algorithm creates a list of all unit normals of the nodes of the triangles.
processing
- Read in data. The algorithm first selects two consecutive slices A i and A i + 1 from the entered voxel model.
- Form a cube. Then the algorithm forms a cube from four neighboring nodes of the disk A i that form a square and the four directly opposite nodes of the disk A i + 1 . The eight corners of the cube are numbered as v 1 ,…, v 8 , the twelve edges as e 1 ,…, e 12 ; v stands for vertex , "node", e for edge , "edge" (see figure).
- Calculate the index of the cube. An index is now formed from the voxel values of the eight nodes: If v i > ρ, then the i-th digit is a 1, otherwise a 0. This results in an eight-digit number, the digits of which are 0 or 1, in the example on the right 10100101. If you consider this as a binary number and convert it into a decimal number, you get the desired index i ∈ {0, 1,…, 255}.
- Create required edges. Look up the entry i in the Triangle Lookup Table, i.e. TLT (i). Create all triangles given there.
- Interpolate surface intersections. Find the position of each node of the triangles you just created on the edges of the cube by linear interpolation of the adjacent corners.
- Calculate and interpolate unit normals. Calculate the unit normals for each corner of the cube and interpolate the unit normals of the nodes of the triangles just created by linear interpolation between the unit normals of the adjacent cube corners.
- Output data. Add the created triangles and the associated unit normals to the list of all triangles and unit normals found so far and march on to the next cube.
output
- D , the list of all triangle nodes created.
- N , the list of all unit normals in the triangle nodes.
Improvements
The algorithm for marching cubes shown above is very rudimentary. For example, it does not take advantage of the fact that information that has already been calculated can be used again: If two neighboring cubes share an edge, the nodes on them only need to be interpolated once; the neighbor can simply take over the nodes already found.
Since the running time of the algorithm only depends on the number of cubes considered, the greatest potential for savings lies in reducing this number. Further optimization approaches therefore try to filter out those cubes from the data volume that do not come into contact with the isosurface before the Marching Cubes run. These are the cubes that are completely inside or completely outside the object.
Octree
A method proposed by Wilhelms / van Gelder in 1992 is to store the volume in an octree . In an octree, each cube of voxels is usually broken down into eight sub-cubes. The lowest and highest values that can be found in it are now saved for each cube. If both values are the same for a cube, it is no longer subdivided. The result is a hierarchy of shrinking cubes for which their value interval is known. By traversing this hierarchy, it is now possible to sort out those cubes whose minimum is above or whose maximum is below the ISO threshold.
The method has the disadvantages that each time the iso value is changed, the hierarchy has to be run through completely again and that in realistic data records, which are usually centered, cubes can usually only be ignored at the lower hierarchy levels.
Approximation by discretization
This is a simplification of the Marching Cube algorithm: the interpolation of the isosurface intersections mentioned in the above description of the algorithm is omitted. The corner points of the triangles generated by the algorithm are then only the center points of the twelve edges of the cube and its center. The surface normals then no longer have to be interpolated, but can also be stored in a look-up table. One advantage of this approximation is that only integer calculations have to be carried out. In addition, you get many coplanar triangular surfaces, which significantly reduces the number of triangular surfaces that result.
Software patents
The MC algorithm is an example of the effects of software patents . Because the algorithm was patented, it could not be used for many years without paying fees to the developer. Therefore, the Marching Tetrahedrons was developed as an alternative , which divided the voxel cubes into tetrahedra and otherwise worked the same. Granted patent US 4,710,876 was filed on June 5, 1985 and was valid in the United States for 20 years.
Web links
Individual evidence
- ^ William E. Lorensen, Harvey E. Cline: Marching Cubes: A high resolution 3D surface construction algorithm. In: Computer Graphics , Vol. 21, No. 4, July 1987, pp. 163-169
- ↑ Timothy S. Newman, Hong Yi: A survey of the marching cubes algorithm In: Computer Graphics , Vol. 30, No. 5, October 2006, pp. 854-879
- ↑ Jane Wilhelms, Allen van Gelder: Octrees for Faster Isosurface Generation . In: ACM Transactions on Graphics (TOG) , Vol. 11, No. 3, pp. 201-227, July 1992
- ↑ C. Montani, R. Scateni, R. Scopigno: Discretized Marching Cubes In: Visualization '94 Proceedings , IEEE Computer Society Press, 1994, pp. 281-287
- ^ System and method for the display of surface structures contained within the interior region of a solid body. Retrieved June 20, 2020 (English).